In a recreational event at a school, there were 8 students, 6 parents, and 4 teachers. To play a game, two members were selected randomly one after the other.
Find the probability distribution of the number of students. Show your steps.
To find the probability distribution of the number of students selected when two members are chosen randomly from a group of 8 students, 6 parents, and 4 teachers, we will follow these steps:
Step 1: Determine the total number of members
First, we need to calculate the total number of members in the group.
Total members=Number of students+Number of parents+Number of teachers
Total members=8+6+4=18
Step 2: Define the random variable
Let X be the random variable representing the number of students selected. The possible values for X when selecting 2 members are:
- X=0 (no students selected)
- X=1 (one student selected)
- X=2 (two students selected)
Step 3: Calculate probabilities for each value of X
Case 1: X=0 (no students selected)
This means both selected members are either parents or teachers. The number of ways to choose 2 members from the 10 non-students (6 parents + 4 teachers) is given by:
Ways to choose 2 from 10=(102)=10×92×1=45
The total ways to choose any 2 members from 18 is:
Total ways to choose 2 from 18=(182)=18×172×1=153
Thus, the probability P(X=0) is:
P(X=0)=Ways to choose 0 studentsTotal ways to choose 2=45153=1551=517
Case 2: X=1 (one student selected)
This means one member is a student and the other is either a parent or a teacher. The number of ways to choose 1 student from 8 and 1 non-student from 10 is:
Ways to choose 1 student from 8=(81)=8
Ways to choose 1 non-student from 10=(101)=10
Thus, the total ways to choose 1 student and 1 non-student is:
Total ways=8×10=80
Therefore, the probability P(X=1) is:
P(X=1)=80153
Case 3: X=2 (two students selected)
This means both selected members are students. The number of ways to choose 2 students from 8 is:
Ways to choose 2 from 8=(82)=8×72×1=28
Thus, the probability P(X=2) is:
P(X=2)=28153
Step 4: Summarize the probability distribution
Now we can summarize the probability distribution of X:
P(X=0)=517P(X=1)=80153P(X=2)=28153
Step 5: Verify the total probability
Finally, we can verify that the total probability sums to 1:
P(X=0)+P(X=1)+P(X=2)=517+80153+28153
Converting 517 to a common denominator of 153:
517=5×917×9=45153
Now summing:
45153+80153+28153=153153=1
Final Probability Distribution
The final probability distribution is:
P(X=0)=517P(X=1)=80153P(X=2)=28153
First, we need to calculate the total number of members in the group.
Total members=8+6+4=18
Let X be the random variable representing the number of students selected. The possible values for X when selecting 2 members are:
- X=0 (no students selected)
- X=1 (one student selected)
- X=2 (two students selected)
This means both selected members are either parents or teachers. The number of ways to choose 2 members from the 10 non-students (6 parents + 4 teachers) is given by:
This means one member is a student and the other is either a parent or a teacher. The number of ways to choose 1 student from 8 and 1 non-student from 10 is:
Ways to choose 1 non-student from 10=(101)=10
This means both selected members are students. The number of ways to choose 2 students from 8 is:
Now we can summarize the probability distribution of X:
Finally, we can verify that the total probability sums to 1:
The final probability distribution is:
Topper's Solved these Questions
Similar Questions
Out of 200 students from a school, 135 like Kabaddi and the remaining students do not like the game. If one student is selected at random from all the students, find the probability that the student selected doesn't like Kabaddi.
View SolutionTickets are numbered from 1 to 10. Two tickets are drawn one after the other art random. Find the probability that the number on one of the tickets is a multiple of 5 and on the other a multiple of 4.
View Solution
Knowledge Check
Two numbers are chosen at random from {1, 2, 3, 4, 5, 6} at a time. The probability that the smaller of the two is less than 4, is
A4/5B1/15C1/5D14/15Two numbers are chosen at random from {1, 2, 3, 4, 5, 6} at a time. The probability that the smaller of the two is less than 4, is
A4/5B1/15C1/5D14/15Two numbers are selected randomly from the set S={1,2,3,4,5,6} without replacement. The probability that minimum of the two numbers is less than 4, is
A1/15B14/15C1/5D4/5
The table given below shows the number of students who were absent and percentage of students who were present in the given two examinations from five different schools. The table shows the percentage of students who were present in the Biology and Physics examination respectively.
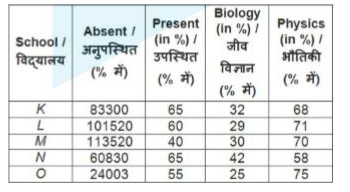
If the number of students who were present in the Physics examination from school A is 250% of the difference of the number of the students who were present in Physics and Biology examination, from school K, then what is the ratio of the number of students who were present from school L to number of students who were present in Physics examination from school A?
View SolutionThe table given below shows the number of students who were absent and percentage of students who were present in the given two examinations from five different schools. The table also shows the percentage of students who were present in the Biology and Physics examination respectively.
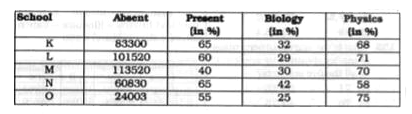
If the number of students who were present in the Physics examination from school A is 250% of the difference of the number of the students who were present in Physics and bilogy examination, from school K, then what is the ratio of the number of students who were present from school L to number of students who were present in Physics examination from school A?
View SolutionThe table given below shows the number of students who were absent and percentage of students who were present in the given two examinations from five different schools. The table also shows the percentage of students who were present in the Biology and Physics examination respectively.
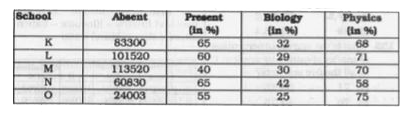
What is the average of the number of the students who were of the students who were present in Physics examination from schools N. K and L?
View SolutionTwo numbers are selected randomly from the set S={1,2,3,4,5,6} without replacement one by one. The probability that minimum of the two numbers is less than 4 is 1/15 b. 14/15 c. 1/5 d. 4/5
View SolutionThe given table shows the number of students participating in various activities in a school.

From the above information one student is chosen. Find the probability that the student participates in games.
View Solution
