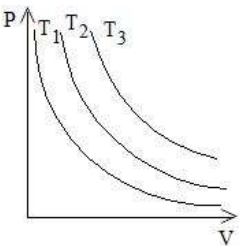
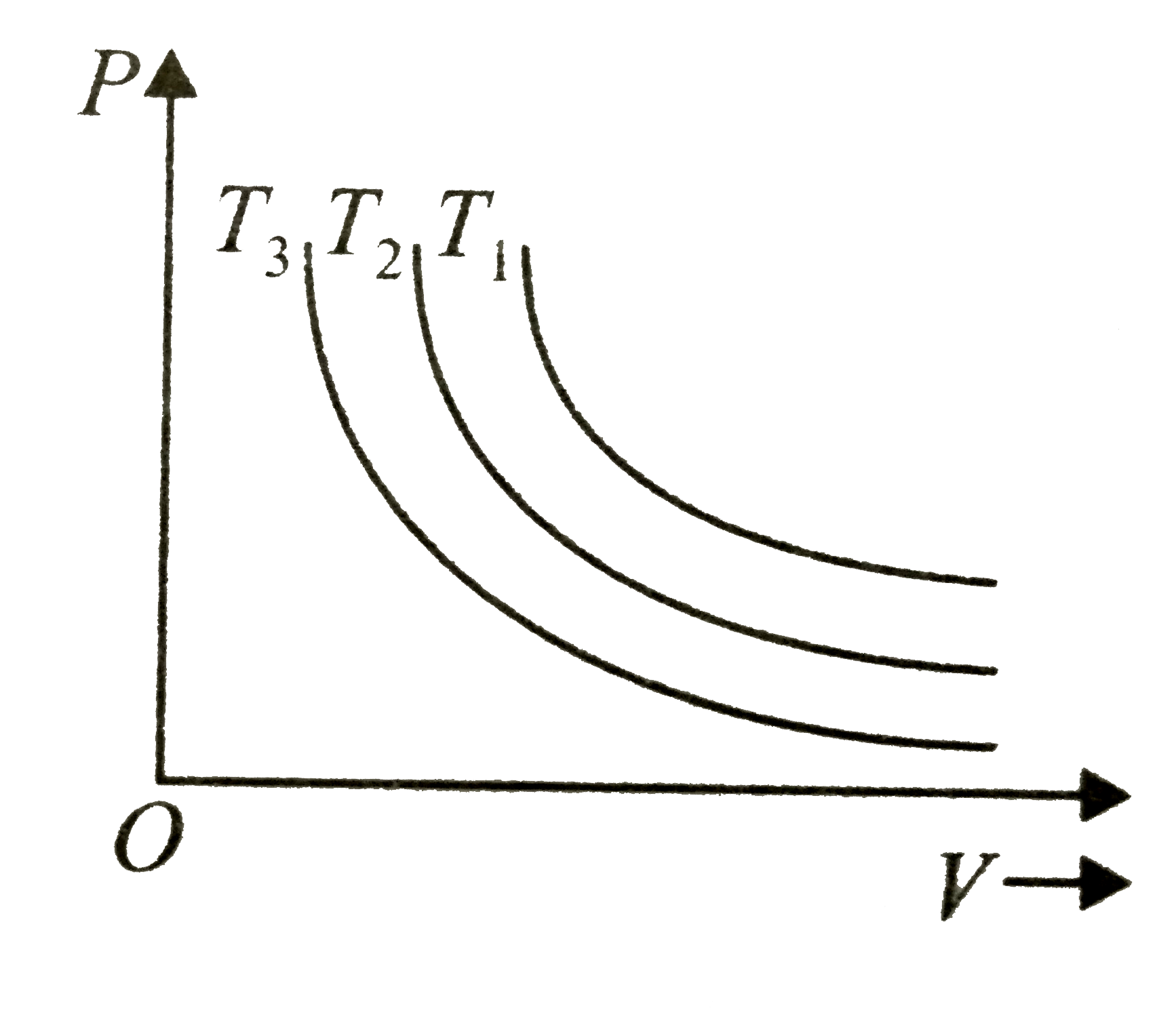
In an isothermal change, the change in perssure and volume of a gas can be repsented for three diffrent temperature : T3>T2>T1 as:
To solve the problem regarding the isothermal change in pressure and volume of a gas at different temperatures, we can follow these steps:
1. Understand the Ideal Gas Law:
The ideal gas law is given by the equation:
PV=nRT
where P is pressure, V is volume, n is the number of moles of gas, R is the ideal gas constant, and T is the absolute temperature.
2. Isothermal Process:
In an isothermal process, the temperature remains constant. Therefore, for a given amount of gas, nRT is constant. This means that:
PV=constant
3. Relationship Between Pressure and Volume:
From the equation PV=constant, we can express pressure P in terms of volume V:
P=constantV
This indicates that pressure is inversely proportional to volume, which means as volume increases, pressure decreases, and vice versa.
4. Effect of Temperature on Pressure:
For different temperatures T1<T2<T3:
- At temperature T1:
P1=nRT1V
- At temperature T2:
P2=nRT2V
- At temperature T3:
P3=nRT3V
5. Comparing Pressures:
Since T3>T2>T1, it follows that:
P1<P2<P3
This is because pressure is directly proportional to temperature when volume is constant.
6. Conclusion:
Therefore, the relationship between the pressures at different temperatures can be summarized as:
P1<P2<P3
This indicates that the pressure increases with an increase in temperature.
Final Answer:
The correct option that represents the relationship of pressures at different temperatures is:
- P1<P2<P3
The ideal gas law is given by the equation:
PV=nRT
where P is pressure, V is volume, n is the number of moles of gas, R is the ideal gas constant, and T is the absolute temperature.
In an isothermal process, the temperature remains constant. Therefore, for a given amount of gas, nRT is constant. This means that:
PV=constant
From the equation PV=constant, we can express pressure P in terms of volume V:
P=constantV
This indicates that pressure is inversely proportional to volume, which means as volume increases, pressure decreases, and vice versa.
For different temperatures T1<T2<T3:
- At temperature T1:
P1=nRT1V
- At temperature T2:
P2=nRT2V
- At temperature T3:
P3=nRT3V
Since T3>T2>T1, it follows that:
P1<P2<P3
This is because pressure is directly proportional to temperature when volume is constant.
Therefore, the relationship between the pressures at different temperatures can be summarized as:
P1<P2<P3
This indicates that the pressure increases with an increase in temperature.
The correct option that represents the relationship of pressures at different temperatures is:
- P1<P2<P3
Topper's Solved these Questions
Similar Questions
Isothermal curves for a given mass of gas are shown at two different temperture T1andT2 in Fig. State whether T1>T2orT2>T1. Justify your answer.
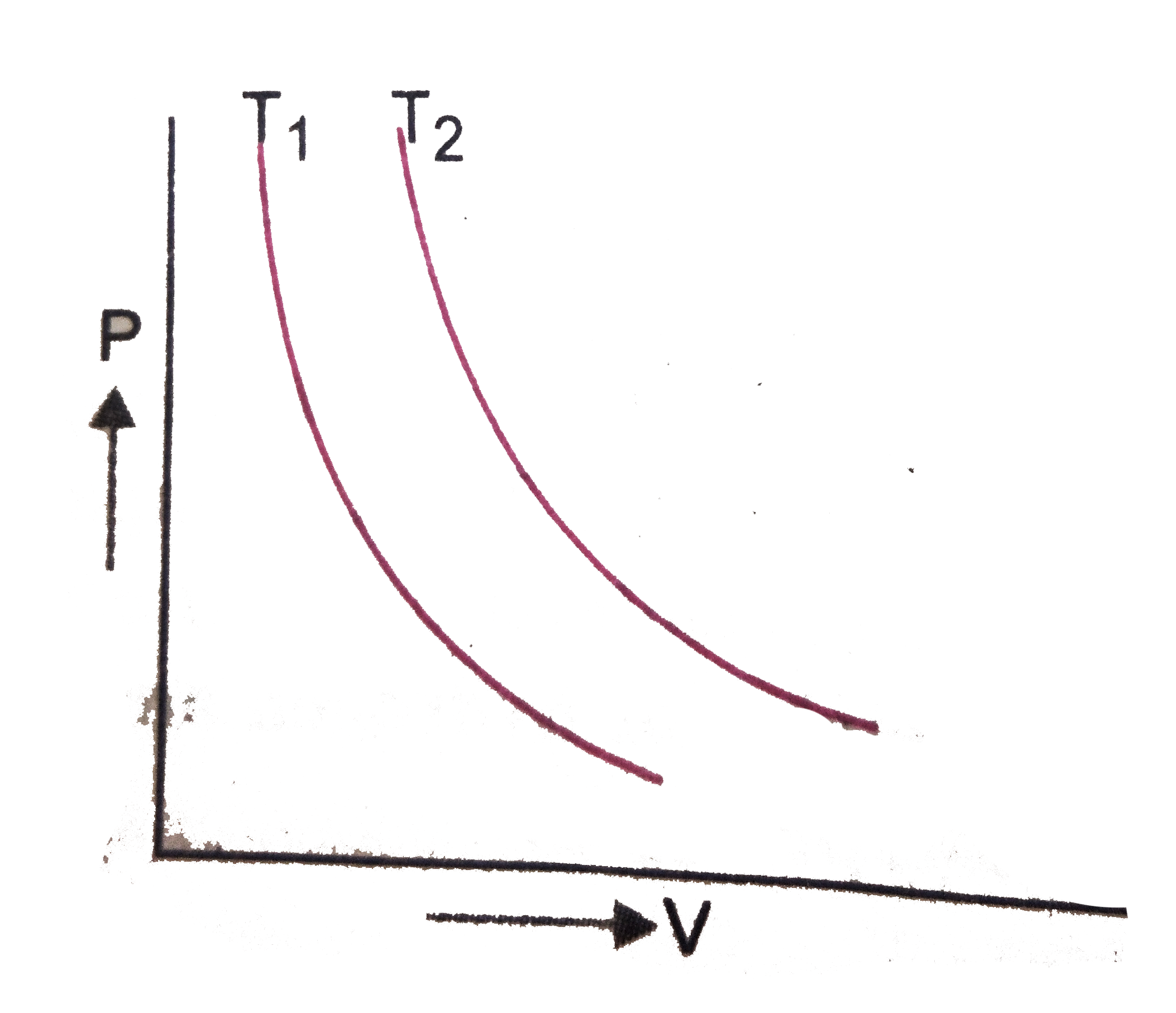
View SolutionIsothermal curves for a given mass of gas are shown at two different temperture T1andT2 in Fig. State whether T1>T2orT2>T1. Justify your answer.

View Solution
Knowledge Check
Coefficient of performance of an ideal refrigerator working between temperature T1 and T2(T1>T2) is
Aβ=T2T1−T2Bβ=T2T1+T2Cβ=T1T1−T2Dβ=T1T1+T2The efficiency of an ideal heat engine working between the temperatureT1 and T2(T1>T2) is
A1−T1T2B1−T2T1C1+T2T1DT2T1For an ideal gas,
(i) the change in internal energy in a constant pressure process from temperature T1 to T2 is equal to nCV(T2−T1), where CV is the molar heat capacity at constant volume and n is the number of moles of the gas
(ii) The change in internal enregy of the gas and the work done by the gas are equal in magnitude in an adiabatic process.
(iii) The internal energy does not change in an isothermal process. ltbr> (iv) no heat is added or removed in an adiabatic processA(i),(iii)B(ii),(iii)C(iii),(iv)Dall
Figure shows the isotherms of a fixed mass of an ideal gas at three temperatures TA,TB and TC , then

View SolutionThe most probable speed of the molecules in a gas at temperature T2 is equal to the average speed of the molecules at temperature T1 Find T2/T1
View SolutionThe isothermal diagram of a gas at three different temperatures T1,T2and_(3), is show in the given figure .Then
View SolutionA solid whose volume does not change with temperature floats in a liquid. For two different temperatures t1 and t2 of the liqiud, fraction f1 and f2 of the volume of the solid remain submerged in the liquid. The coefficient of volume expansion of the liquid is equal to
View SolutionWhen 1mol of a monoatomic ideal gas at TK undergoes adiabatic change under a constant external pressure of 1atm, changes volume from 1L→2L. The final temperature (in K) would be
View Solution
