A parallel plate capacitor has plate area 40cm2 and plates separation 2mm. The space between the plates is filled with a dielectric medium of a thickness 1 mm and dielectric constant 5. The capacitance of the system is :
103ε0F
310ε0F
24ε0F
10ε0F
The correct Answer is:A
To solve the problem of finding the capacitance of a parallel plate capacitor with a dielectric medium, we can break it down into several steps.
Step 1: Identify Given Values
- Plate area A=40cm2=40×10−4m2
- Plate separation d=2mm=2×10−3m
- Thickness of dielectric d1=1mm=1×10−3m
- Dielectric constant k=5
Step 2: Calculate Capacitance with Dielectric
The capacitance C1 of the section filled with the dielectric can be calculated using the formula:
C1=kϵ0Ad1
Where ϵ0 is the permittivity of free space, approximately 8.85×10−12F/m.
Substituting the values:
C1=5×(8.85×10−12)×(40×10−4)1×10−3
Calculating C1:
C1=5×8.85×40×10−161×10−3=5×8.85×401×10−13
C1=20×8.85×10−13=177×10−13F=1.77×10−12F
Step 3: Calculate Capacitance without Dielectric
The remaining gap d2 is:
d2=d−d1=2×10−3−1×10−3=1×10−3m
The capacitance C2 of the section without the dielectric is:
C2=ϵ0Ad2
Substituting the values:
C2=(8.85×10−12)×(40×10−4)1×10−3
Calculating C2:
C2=8.85×40×10−161×10−3=354×10−13F=3.54×10−12F
Step 4: Combine Capacitances in Series
Since C1 and C2 are in series, the equivalent capacitance Ceq is given by:
1Ceq=1C1+1C2
Substituting the values:
1Ceq=11.77×10−12+13.54×10−12
Calculating:
1Ceq=3.54+1.771.77×3.54×1012
Calculating the numerator:
1Ceq=5.316.25×10−24=0.8496×1012
Thus:
Ceq≈10.8496×1012≈1.176×10−12F
Final Step: Summary of Capacitance
The equivalent capacitance of the system is approximately:
Ceq≈103ϵ0F
- Plate area A=40cm2=40×10−4m2
- Plate separation d=2mm=2×10−3m
- Thickness of dielectric d1=1mm=1×10−3m
- Dielectric constant k=5
The capacitance C1 of the section filled with the dielectric can be calculated using the formula:
C1=kϵ0Ad1
Where ϵ0 is the permittivity of free space, approximately 8.85×10−12F/m.
C1=5×(8.85×10−12)×(40×10−4)1×10−3
Calculating C1:
C1=5×8.85×40×10−161×10−3=5×8.85×401×10−13
C1=20×8.85×10−13=177×10−13F=1.77×10−12F
The remaining gap d2 is:
d2=d−d1=2×10−3−1×10−3=1×10−3m
The capacitance C2 of the section without the dielectric is:
C2=ϵ0Ad2
Substituting the values:
C2=(8.85×10−12)×(40×10−4)1×10−3
Calculating C2:
C2=8.85×40×10−161×10−3=354×10−13F=3.54×10−12F
Since C1 and C2 are in series, the equivalent capacitance Ceq is given by:
1Ceq=1C1+1C2
Substituting the values:
1Ceq=11.77×10−12+13.54×10−12
Calculating:
1Ceq=3.54+1.771.77×3.54×1012
Calculating the numerator:
1Ceq=5.316.25×10−24=0.8496×1012
Thus:
Ceq≈10.8496×1012≈1.176×10−12F
The equivalent capacitance of the system is approximately:
Ceq≈103ϵ0F
Topper's Solved these Questions
Similar Questions
The capacitance of a parallel plate capacitor with plate area A and separation d is C. The space between the plates in filled with two wedges of dielectric constants K1 and K2 respectively. Find the capacitance of resulting capacitor.
 View Solution
View SolutionThe capacitance of a parallel plate capacitor with plate area A and separation d is C. The space between the plates in filled with two wedges of dielectric constants K1 and K2 respectively. Find the capacitance of resulting capacitor.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A parallel plate capacitor has plate area A and plate separation d. The space between the plates is filled up to a thickness x<d with a dielectric constant K. Calculate the capacitance of the system.
 A2KεAKd−x(K−1)BKεAK2d−x(K−1)CKεAK−x(K−1)DKεAKd−x(K−1)
A2KεAKd−x(K−1)BKεAK2d−x(K−1)CKεAK−x(K−1)DKεAKd−x(K−1) - Question 2 - Select One
A parallel plate air capacitor has capacitance C. Half of space between the plates is filled with dielectric of dielectric constant K as shown in figure . The new capacitance is C . Then
 AC=C[KK+1]BC'=C[2KK+1]CC'=2CK+1DC'=C[1+K2]
AC=C[KK+1]BC'=C[2KK+1]CC'=2CK+1DC'=C[1+K2] - Question 3 - Select One
A parallel plate capacitor with air between the plates has a capacitance C. If the distance between the plates is doubled and the space between the plates is filled with a dielectric of dielectric constant 6, then the capacitance will become.
A3CBC3C12 CDC6
Fig shows a parallel plate capacitor of plate area A and plate separation d. Its entire space is filled with three different dielectric slabs of same thickness. Find the equivalent capacitance of the arrangment.
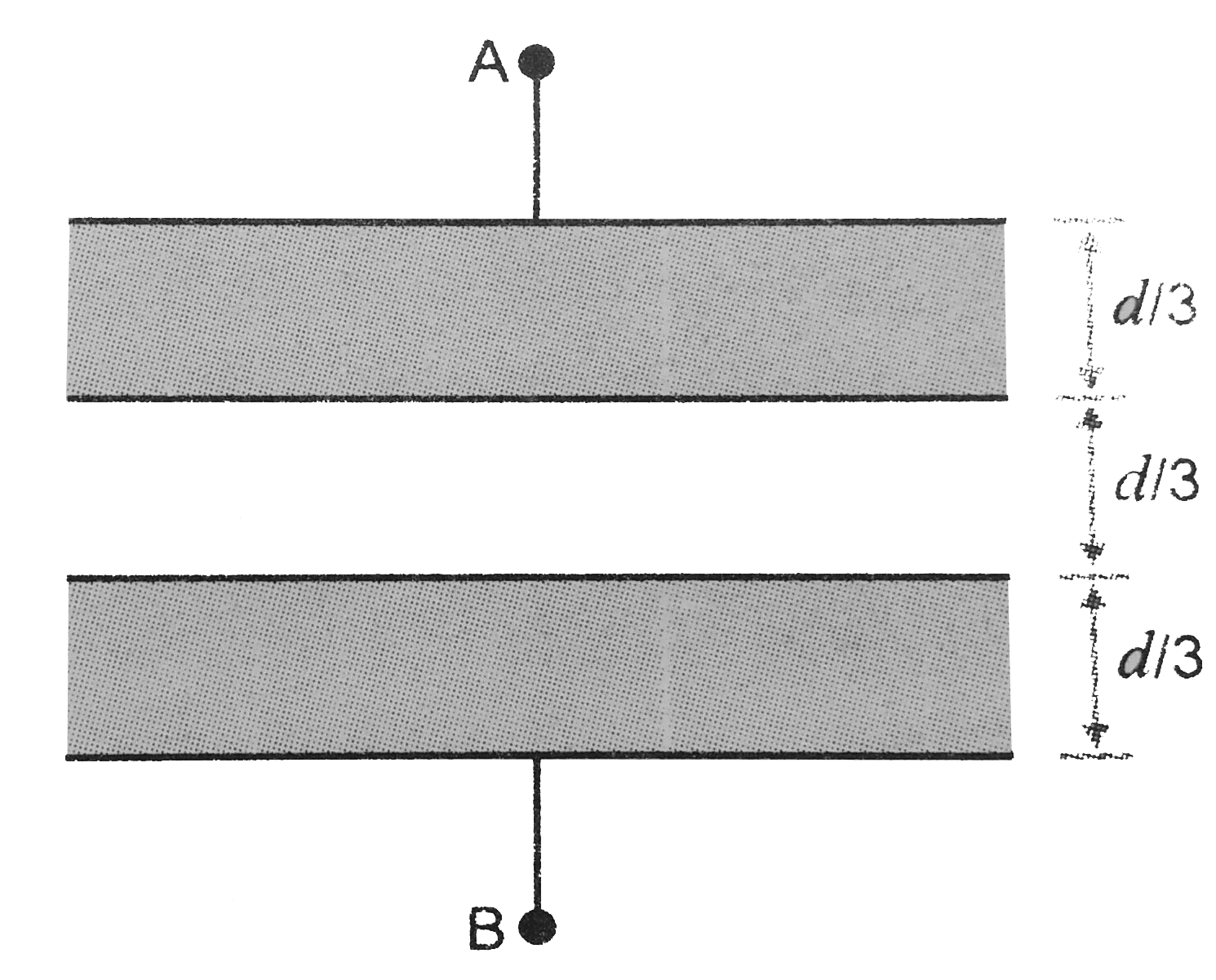 View Solution
View SolutionTwo parallel plate capacitors, each of capacitance 40 muF, are connected is series. The space between the plates of one capacitor is filled with a dielectric material of dielectric constant K =4. Find the equivalent capacitacne of the system.
View SolutionA parallel plate capacitor has plate area of A separated by distance between them. It is completely filled with dielectric medium, its dielectric constant increases linearly as move from one plate to other plate from k1 to k2 . Then the capacitance of system is given by :
 View Solution
View SolutionA parallel plate capacitor has a capacity C. The separation between plates is doubled and a dielectric medium is inserted between plates. The new capacity is 3C. The dielectric constant of medium is
View SolutionA parallel plate air capacitor has capacitance 18μF. If the distance between the plates is tripled and dielectric medium is introduced the capacitance becomes 72μF. The dielectric constant of the medium is :-
View Solution

