Two equal positive point charges are separated by a distance .The distance of a point from the centre of the line joining two charges on the equatorial line (perpendicular bisector) at which force experienced by a test charge becomes maximum is .The value of is _____
To solve the problem, we need to find the distance y from the center of the line joining two equal positive point charges Q separated by a distance 2a where the force experienced by a test charge q0 becomes maximum.
1. Understanding the Configuration:
- We have two equal positive charges Q located at points A and B such that the distance between them is 2a.
- The center of the line joining the two charges is point O, which is at a distance a from each charge.
- We are interested in the point P on the perpendicular bisector (equatorial line) at a distance y from point O.
2. Force Calculation:
- The force F on the test charge q0 due to one charge Q at point P can be expressed using Coulomb's law:
F=k⋅Q⋅q0r2
- Here, r is the distance from charge Q to the point P. By the Pythagorean theorem, this distance is:
r=√a2+y2
3. Net Force on the Test Charge:
- The net force Fnet on q0 due to both charges can be calculated. The components of the forces due to each charge along the vertical direction will add up, while the horizontal components will cancel out.
- The vertical component of the force from each charge is:
Fvertical=F⋅cos(θ)
- The angle θ can be defined as:
tan(θ)=ya
- Therefore, cos(θ)=a√a2+y2.
4. Expression for Net Force:
- The net force Fnet is:
Fnet=2⋅F⋅cos(θ)=2⋅k⋅Q⋅q0(a2+y2)⋅a√a2+y2=2k⋅Q⋅q0⋅a(a2+y2)3/2
5. Maximizing the Force:
- To find the maximum force, we differentiate Fnet with respect to y and set the derivative to zero:
dFnetdy=0
- This leads to the equation:
(a2+y2)3/2−3y2(a2+y2)1/2=0
- Simplifying gives:
a2+y2−3y2=0⇒a2−2y2=0⇒y2=a22
6. Finding the Value of x:
- From the problem statement, we have y=a√x.
- Since y2=a22, we can equate:
a2x=a22⇒x=2
Final Answer:
The value of x is 2.
- We have two equal positive charges Q located at points A and B such that the distance between them is 2a.
- The center of the line joining the two charges is point O, which is at a distance a from each charge.
- We are interested in the point P on the perpendicular bisector (equatorial line) at a distance y from point O.
- The force F on the test charge q0 due to one charge Q at point P can be expressed using Coulomb's law:
F=k⋅Q⋅q0r2
- Here, r is the distance from charge Q to the point P. By the Pythagorean theorem, this distance is:
r=√a2+y2
- The net force Fnet on q0 due to both charges can be calculated. The components of the forces due to each charge along the vertical direction will add up, while the horizontal components will cancel out.
- The vertical component of the force from each charge is:
Fvertical=F⋅cos(θ)
- The angle θ can be defined as:
tan(θ)=ya
- Therefore, cos(θ)=a√a2+y2.
- The net force Fnet is:
Fnet=2⋅F⋅cos(θ)=2⋅k⋅Q⋅q0(a2+y2)⋅a√a2+y2=2k⋅Q⋅q0⋅a(a2+y2)3/2
- To find the maximum force, we differentiate Fnet with respect to y and set the derivative to zero:
dFnetdy=0
- This leads to the equation:
(a2+y2)3/2−3y2(a2+y2)1/2=0
- Simplifying gives:
a2+y2−3y2=0⇒a2−2y2=0⇒y2=a22
- From the problem statement, we have y=a√x.
- Since y2=a22, we can equate:
a2x=a22⇒x=2
The value of x is 2.
Topper's Solved these Questions
Similar Questions
Two point charges 4μCand−2μC are separated by a distance of 1m in air. Calculate at what point on the line joining the two charges is the electric potential zero ?
View SolutionTwo point charges +4μCand+1μC are separated by a distance of 2 m in air. Find the point on the line joining the two charges at which the net electric field of the system is zero.
View Solution
Knowledge Check
Two point charges Q and −Q/4 are separated by a distance X. Then
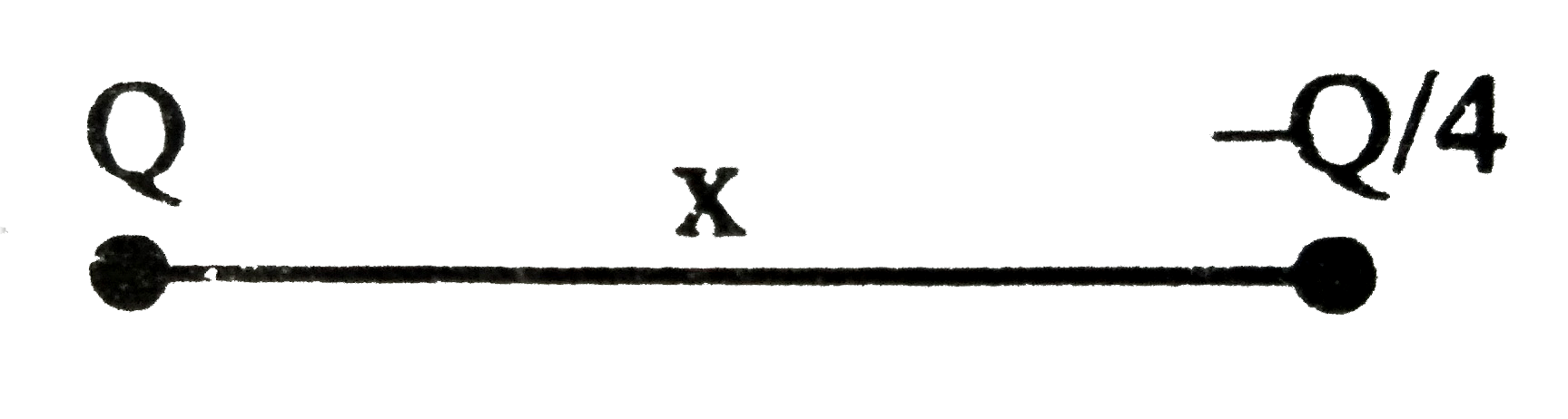 .Apotential is zero at a point on the axis which is x/3 on the right side of the cahrge −q/4Bpotential is zero at a point on the axis which is x/5 on the left side fo the charge −Q/4Celectric field is zero at a point on the axis which is at a distance x on the right side fo the charge −Q/4Dthere exist two points on the axis where electric field is zero.
.Apotential is zero at a point on the axis which is x/3 on the right side of the cahrge −q/4Bpotential is zero at a point on the axis which is x/5 on the left side fo the charge −Q/4Celectric field is zero at a point on the axis which is at a distance x on the right side fo the charge −Q/4Dthere exist two points on the axis where electric field is zero.Two positive point charges are separated by a distance R. If the distance between the charges is reduced to R/2, what happens to the total electric potential energy of the system?
AIt is doubledBIt is reduced to one-half of its original valueCIt remains the sameDIt is reduced to one-fourth of its original valueThe two point charges 4μC and 1μC are separated by a distance of 2 m in air. Find the point on the line joining the charges at which net electric field of the system is zero.
A43m from 1μCB23m from 1μCC43m from 4μCD23m from 4μC
Two point charges +4μCand−2μC are separated by a distance of 1 m in air. Calculate at what point on the line joining the two charges is the electric potential zero.
View SolutionTwo charge +aq and -q are kept apart. Then , at any point on the right bisector of line joining the two charge
View SolutionTwo point charges+ q and-q are placed at distanced apart. What are the points at which the resultant field is parallel to the line joining the two charges ?
View SolutionTwo equal charges q of opposite sign are separated by a small distance 2a,The electric intensity E at a point on the perpendicular bisector of theline joining the two charges at a very large distance r form the line is
View SolutionTwo positive point charges q1=16μC and q2=4μC are separated in vacuum by a distance of 3.0m. Find the point on the line between the charges where the net electric field is zero.-
View Solution
