A body of mass 500 g moves along x-axis such that it's velocity varies with displacement x according to the relation v= 10√x m/s the force acting on thebody is
25N
125N
5 N
166N
To solve the problem, we need to find the force acting on a body of mass 500 g as it moves along the x-axis with a velocity given by the equation v=10√x m/s.
1. Convert Mass to Kilograms:
The mass of the body is given as 500 g. We need to convert this to kilograms since the SI unit of mass is kg.
m=500g=500×10−3kg=0.5kg
Hint: Remember to convert grams to kilograms by dividing by 1000.
2. Differentiate the Velocity Function:
We are given the velocity as a function of displacement:
v=10√x
To find the acceleration, we need to differentiate the velocity with respect to time. We can use the chain rule:
a=dvdt=dvdx⋅dxdt=dvdx⋅v
3. Calculate dvdx:
Differentiate v=10√x with respect to x:
dvdx=10⋅12√x=5√x
Hint: When differentiating, remember the power rule and the chain rule.
4. Substitute v into the Acceleration Formula:
Now substitute v into the acceleration formula:
a=dvdx⋅v=(5√x)⋅(10√x)=50m/s2
Hint: Ensure you multiply the derivative by the original velocity correctly.
5. Calculate the Force Using Newton's Second Law:
Now, we can use Newton's second law to find the force:
F=m⋅a
Substitute the values of m and a:
F=0.5kg⋅50m/s2=25N
Hint: Use the formula F=ma to find the force acting on the body.
6. Final Answer:
The force acting on the body is:
F=25N
Therefore, the correct option is Option 1: 25N.
The mass of the body is given as 500 g. We need to convert this to kilograms since the SI unit of mass is kg.
m=500g=500×10−3kg=0.5kg
We are given the velocity as a function of displacement:
v=10√x
To find the acceleration, we need to differentiate the velocity with respect to time. We can use the chain rule:
a=dvdt=dvdx⋅dxdt=dvdx⋅v
Differentiate v=10√x with respect to x:
dvdx=10⋅12√x=5√x
Now substitute v into the acceleration formula:
a=dvdx⋅v=(5√x)⋅(10√x)=50m/s2
Now, we can use Newton's second law to find the force:
F=m⋅a
Substitute the values of m and a:
F=0.5kg⋅50m/s2=25N
The force acting on the body is:
F=25N
Topper's Solved these Questions
Similar Questions
A particle is moving along x-axis such that its velocity varies with time according to v=(3m/s2)t−(2m/s3)t2. Find the velocity at t = 1 s and average velocity of the particle for the interval t = 0 to t = 5 s.
View SolutionIf the velocity of a body related to displacement x is given by v=√5000+24x m/s, then the acceleration of the body is _______m/s2.
View Solution
Knowledge Check
- Question 1 - Select One
A body of mass m starts moving from rest along x-axis so that it velocity varies as v=a√s where a is a constant and s is the distance covered by the body .The total work done by all the forces acting on the body in the first second after the start of the motion is :
A18ma4t2B4ma4t2C8ma4t2D14ma4t2 - Question 2 - Select One
A particle moves along x-axis in such a way that its x-coordinate varies with time t according to the equation x=(8−4t+6t2) metre.
The velocity of the particle will vary with time according to the graph :-A B
B C
C D
D
- Question 3 - Select One
A particle moves along x-axis in such a way that its r-coordinate varies with time't according to the equation x= (8−4t+6t2) metre. The velocity of the particle will vary with time according to the graph
A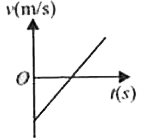 B
B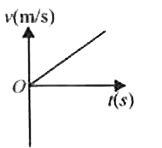 C
C D
D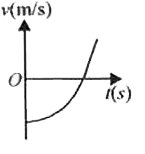
A particle moves along X-axis in such a way that its coordinate X varies with time t according to the equation x=(2−5t+6t2)m. The initial velocity of the particle is
View SolutionA body moves along x-axis such that its displacement varies with time as given, x=7+3t+5t2. The average velocity during 3rd second is
View SolutionA body of mass 1kg is moving along a straight line with a velocity of 1m/s. The external force acting in the body is
View SolutionFor motion of an object along the x-axis the velocity v dipends on the displacement x an v=3x2, then what is the acceleration at x=2m.
View SolutionA particle is moving along x-axis. Its velocity v with x co-ordinate is varying as v=√x. Then
View Solution

