The angle of elevation of the top P of a tower from the feet of one person standing due South of the tower is and from the feet of another person standing due west of the tower is . If the height of the tower is 5 meters, then the distance (in meters) between the two persons is equal to
10
5
To solve the problem, we will use trigonometric relationships in right triangles formed by the tower and the persons standing at different positions.
1. Understanding the Problem:
- Let the tower be represented as AB where A is the foot of the tower and B is the top of the tower.
- The height of the tower AB is given as 5 meters.
- Person P is standing due South of the tower, and the angle of elevation to the top of the tower from P is 45∘.
- Person Q is standing due West of the tower, and the angle of elevation to the top of the tower from Q is 30∘.
2. Finding the Distance from Person P to the Tower:
- From the right triangle ABP:
tan(45∘)=ABAP
Since tan(45∘)=1, we have:
1=5AP⟹AP=5 meters
3. Finding the Distance from Person Q to the Tower:
- From the right triangle ABQ:
tan(30∘)=ABAQ
Since tan(30∘)=1√3, we have:
1√3=5AQ⟹AQ=5√3 meters
4. Finding the Distance Between Persons P and Q:
- The distance PQ between persons P and Q can be calculated using the Pythagorean theorem since AP and AQ are perpendicular to each other:
PQ=√AP2+AQ2
Substituting the values:
PQ=√(5)2+(5√3)2=√25+75=√100=10 meters
Final Answer:
The distance between the two persons is 10 meters.
- Let the tower be represented as AB where A is the foot of the tower and B is the top of the tower.
- The height of the tower AB is given as 5 meters.
- Person P is standing due South of the tower, and the angle of elevation to the top of the tower from P is 45∘.
- Person Q is standing due West of the tower, and the angle of elevation to the top of the tower from Q is 30∘.
- From the right triangle ABP:
tan(45∘)=ABAP
Since tan(45∘)=1, we have:
1=5AP⟹AP=5 meters
- From the right triangle ABQ:
tan(30∘)=ABAQ
Since tan(30∘)=1√3, we have:
1√3=5AQ⟹AQ=5√3 meters
- The distance PQ between persons P and Q can be calculated using the Pythagorean theorem since AP and AQ are perpendicular to each other:
PQ=√AP2+AQ2
Substituting the values:
PQ=√(5)2+(5√3)2=√25+75=√100=10 meters
The distance between the two persons is 10 meters.
Topper's Solved these Questions
Similar Questions
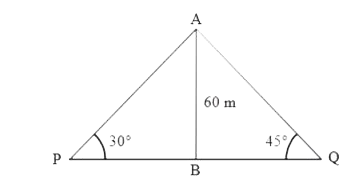
In the figure, two persons are standing at the opposite direction P & Q of the tower. If the height of the tower is 60 m then find the distance between the two persons.
View SolutionThe angle of elevation of the top of a tower at a point on the ground 20 m from the foot of the tower is 30∘. What is the height of the tower?
View Solution
Knowledge Check
The angle of elevation of the top of a tower at a horizontal distance equal to the height of the tower from the base of the tower is
A30∘B45∘C60∘Dany acute angleAt a point 20 m away from the foot of a tower, the angle of elevation of the top of the tower is 30∘ The height of the tower is
A20√3mB20√3mC√320mDNone of theseAt a point 20 m away from the foot of a tower, the angle of elevation of the top of the tower is 30∘ The height of the tower is
A20√3mB20√3mC√320mDNone of these
The angle of elevation of the top of a tower a point A due south of it is 30∘ and from a point B due west of it is 45∘ .If the height of the tower is 100 meters ,then find the distance AB.
View SolutionThe angle of elevation of the peak of a tower from a point P of the land is 30∘ and the angle of elevation of the peak of a flag on the tower is 45∘. If the length of the flag is 5 meters, find the height of the tower.
View SolutionThe angle of elevation of the top of a tower at a point A due south of the tower is α and at β due east of the tower is β. If AB=d, then height of the tower is
View SolutionFrom a point 20 m away from the foot of a tower, the angle of elevation of the top of the tower is 30∘ . The height of the tower is
View SolutionThe angle of elevation of the top of a tower of height H from the foot of another tower in the same plane is 60∘ and the angle of elevation of the top of the second tower from the foot of the first tower is 30∘. If is the height of the other tower is h , then which one of the following is correct?
View Solution
