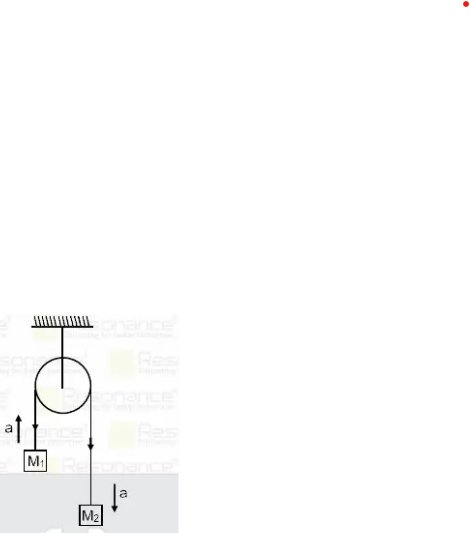
In the given pulley block system
given a = g/8
find the ratio of M1M2=?
78
57
97
79
The correct Answer is:D
Topper's Solved these Questions
Similar Questions
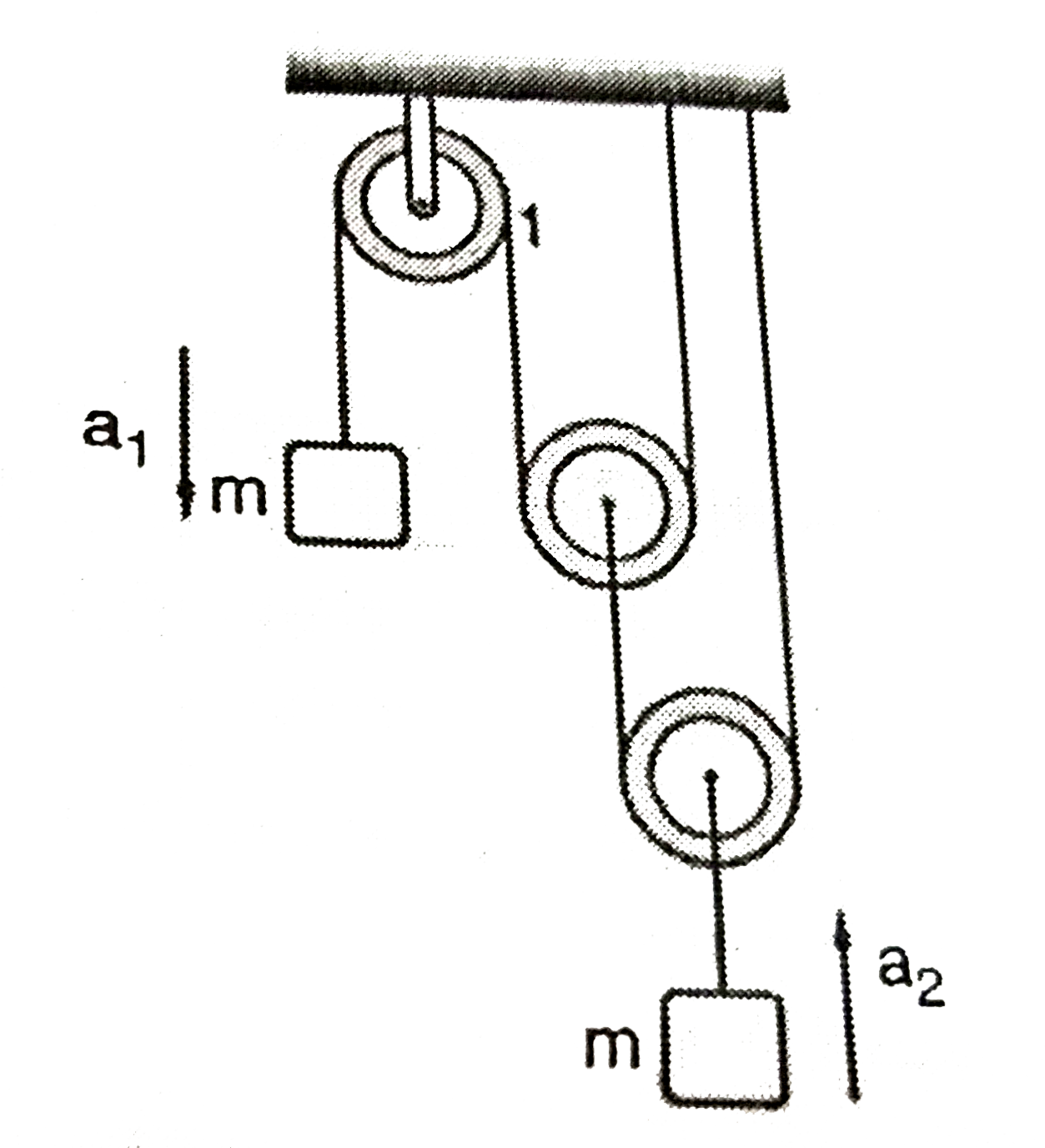
Two blocks of masses m1 and m2 are connected by massless threads. The pulleys are massless and smooth if a1 is the magnitude value of acceleration of m1 and a2 is the magnitude value of acceleration of m2 find the ratio of a1a2
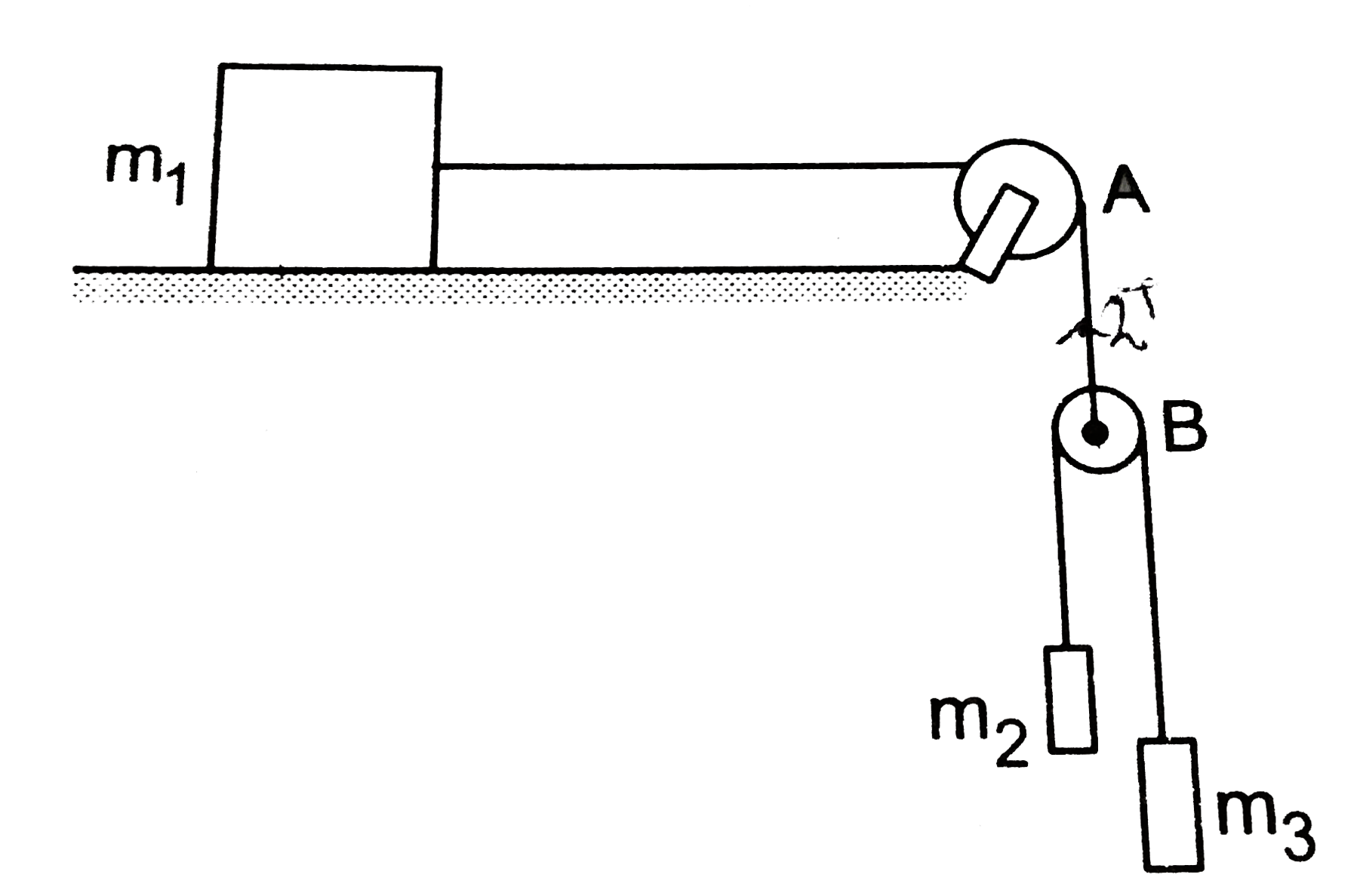
View SolutionThree blocks of masses m1,m2andm3 are connected as shown in the figure. All the surfaces are frictionless and the string and the pulleys are light. Find the acceleration of m1
View Solution
Knowledge Check
A light string passing over a smooth light pulley connects two blocks of masses m1 and m2 (vertically). If the acceleration of the system is g/8, then the ratio of masses is
A8:1B4:3C5:3D9:7A light string passing over a smooth light pulley connects two blocks of masses m1 and m2 (vertically). If the acceleration of the system is g/8, then the ratio of the masses is
A8:1B9:7C4:3D5:3A light string passing over a smooth light pulley connects two blocks of masses m1 and m2 (vertically). If the acceleration of the system is g/8, then the ratio of the masses is
A(a) 8:1B(b) 9:7C(c) 4:3D(d) 5:3
Three blocks of masses m1,m2andm3 are connected as shown in the figure. All the surfaces are frictionless and the string and the pulleys are light. Find the acceleration of m1

View SolutionA light string passing over a smooth light pulley connects two blocks of masses m_(1) and m_(2) (vertically).If the acceleration of the system is g/8 then the ratio of masses "m_(1)" to "m_(2)" is "(" take "m_(1)>m_(2)]
View SolutionA light string passing over a smooth light pulley connects two blocks of masses m1 and m2 (vertically). If the acceleration of the system is g/8, then the ratio of the masses is
View SolutionA light string passing over a smooth light pulley connects two blocks of masses m1 and m2 (vertically). If the acceleration of the system is g/8, then the ratio of the masses is
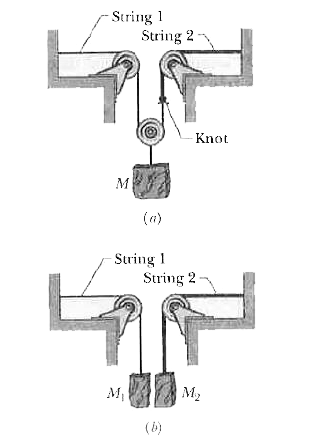
View SolutionIn fig. 16-47a, string 1 has a linear density of 3.00 g/m, and string 2 has a linear density of 5.00 g/m. They are under tension due to the hanging block of mass M= 800 g. Calculate the wave speed on (a) string 1 and (b) string 2 (Hint: When a string loops halfway around a pulley, it pulls on the pulley witii a net force that is twice the tension in the string) Next the block is divided into two blocks (with M1+M2=M) and the apparatus in tearranged as shown in fig. 16-47b. Find (c) M1and(d)M2 such that the wave speeds in the two strings are equal.
View Solution
