Three blocks of masses m1,m2andm3 are connected as shown in the figure. All the surfaces are frictionless and the string and the pulleys are light. Find the acceleration of m1
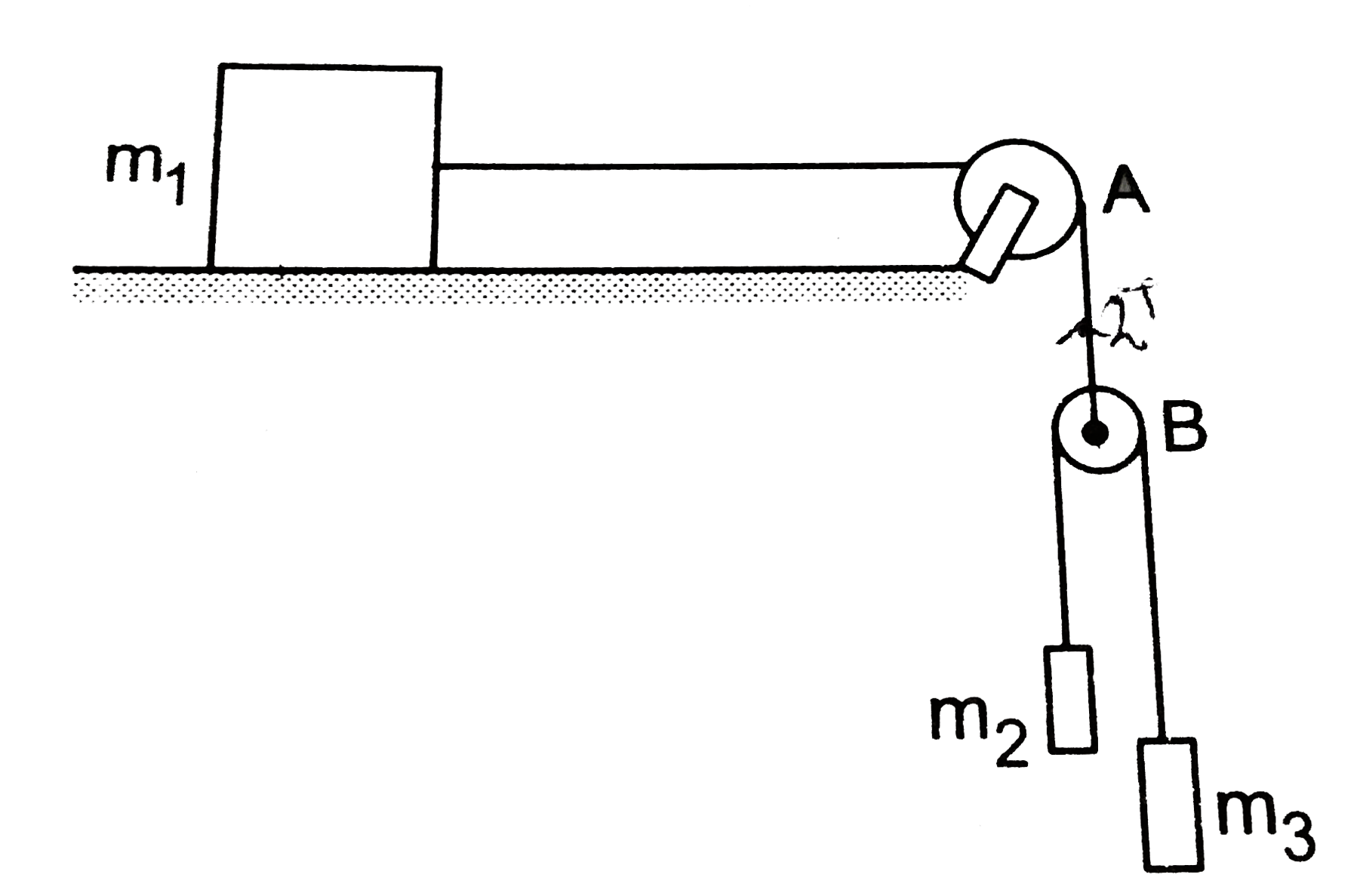
Suppose the acceleration of nq1 is a0 towards right. That will also be the downward acceleration of the pulley B because the string connecting m1andm3 has a constant length. This implies tht the decrease i the separation between m2and B equals the increase in teh separation between m3andB. So, the upward acceleeration of m2 wiht respect to B equals the downward acceleration of m3 with respect of B. Let this acceleration be a
The acceleration of m2 with respect to the ground =a0−a (downward) and the acceleration of m3 with respect to the ground =a0+a (downward).
These accelerations will be used in Newton's laws. Let the tension be T in the upper string and T' in the lower string. consider the motion of the pulley B.
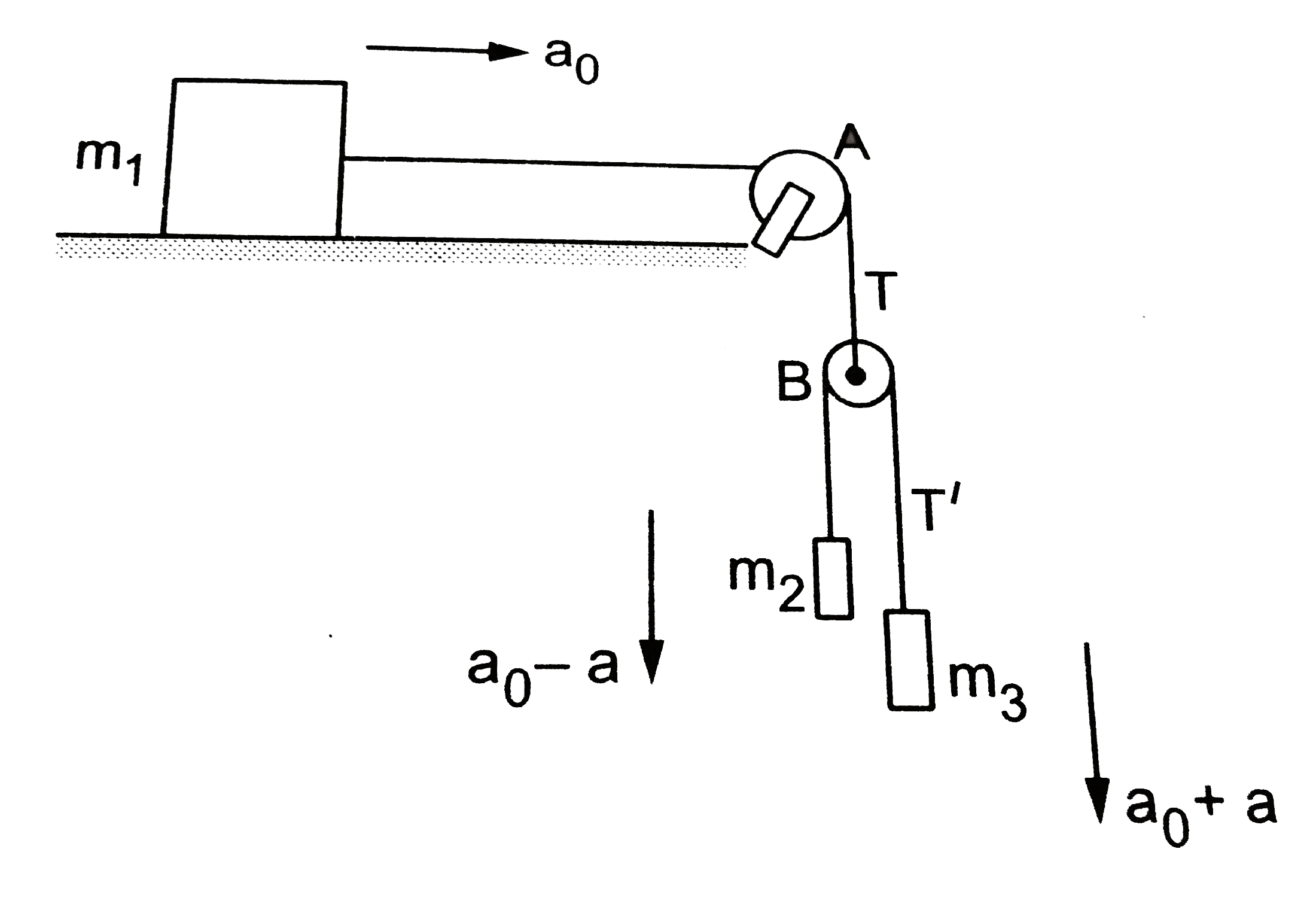
The forces on this light pulley are ltbr> a. T upward by the upper sting and
2T' downwards by thelower string.
As the mass of the pulley is negligible,
2T'−T=0
giving T≡T2............i
Motion m1
THe acceleration is a0 in the horizontal direction. The forces on m1 are
a. T by the string (horizontal)
b. m1 g by theearth (verticlaly downwards) and
N by the table (verrtically upwards).
IN the horizontal direction the equation
T=m1a0
Motion of m2: acceleration is a0−a in the fownward direction. Teh forces on m2 are
a. m2g downward by teh earth and
T'=T2 upward by teh string.
Thus, m2g−T2=m2(a0+a)...........iii
Moton of m3= The aceeleration is (a0+a) downward. The forces on m3 are
a. m3g downward by the earth and
b. T'=T/2 upward by the string. thus,
m3g−T2=m3(a0+0)...........iv.
We want to calculate a0 so we shall elimiN/Ate T and a from ii, iii, and iv.
Putting T from ii in and iii and iv,
a0−a=m2−mI1a02m2=g−m1a02m2
and a0+a+m3g−m−1a02M3=g−m1a02m3
Adding 2a0=2g−m1a02(1m2+1m3)
a0=g−m1a04(1m2+1m3)
or, a0[1+m14(1m−2+1m3)]=g
or,a0=g1+m14(1m2+1m3)
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMACHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Short Answer
17 Videos
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMACHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Objective 1
14 Videos
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMACHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Exercises
42 Videos
- LAWS OF THERMODYNAMICSBOOK - HC VERMACHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Short Answer
15 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMACHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Exercises
34 Videos
Similar Questions
Knowledge Check
Three blocks of masses m1,m2 and M are arranged as shown in figure. All the surfaces are fricationless and string is inextensible. Pulleys are light. A constant force F is applied on block of mass m1. Pulleys and string are light. Part of the string connecting both pulleys is vertical and part of the strings connecting pulleys with masses m1 and m2 are horizontal.
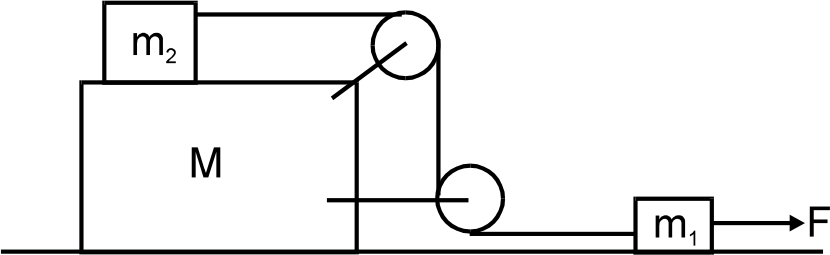
(P)Accleration of mass m1(1)Fm1(Q)Acceleration of massm2(2)Fm1+m2(R)Acceleration of mass M(3)zero(S)Tension in the string(4)m2Fm1+m2APQRS(A)2234BPQRS(B)2134CPQRS(C)2241DPQRS(D)2131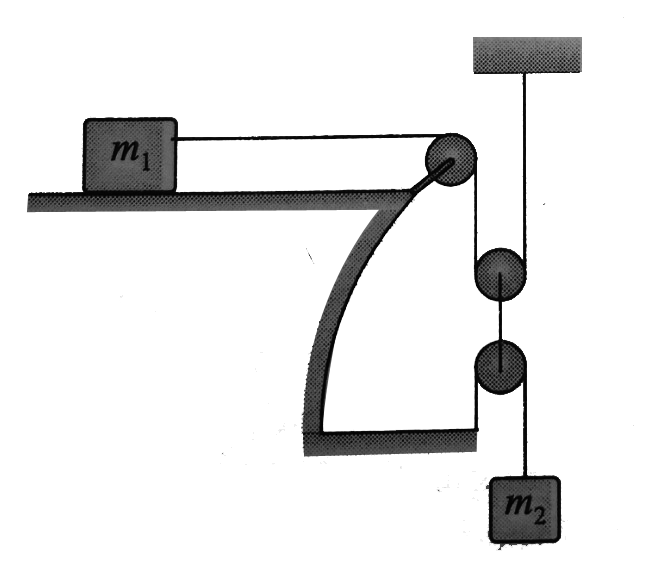
Two blocks of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is :Am2gm1+m2Bm1gm1+m2C4m2g−m1gm1+m2Dm2gm1+4m2Two block of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is:
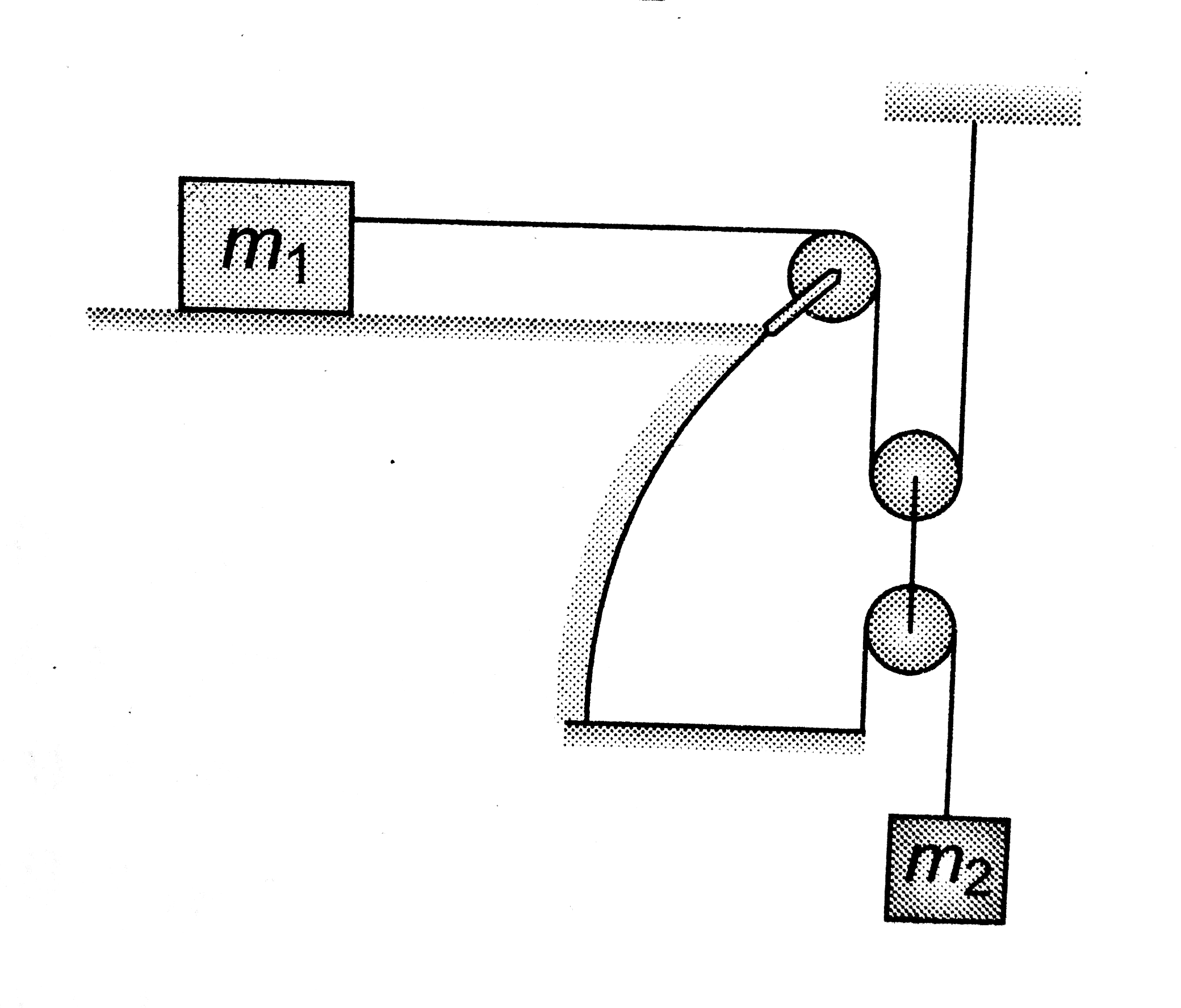 Am2gm1+m2Bm1gm1+m2C4m2g−m1gm1+m2Dm2gm1+4m2
Am2gm1+m2Bm1gm1+m2C4m2g−m1gm1+m2Dm2gm1+4m2
A hanging block of mass m' prevents the smaller block of mass m from slipping over a movable triangular block of mass M. All the surface are frictionless and the strings and the pulleys are light. Value of mass m' in terms of m, M and θ is
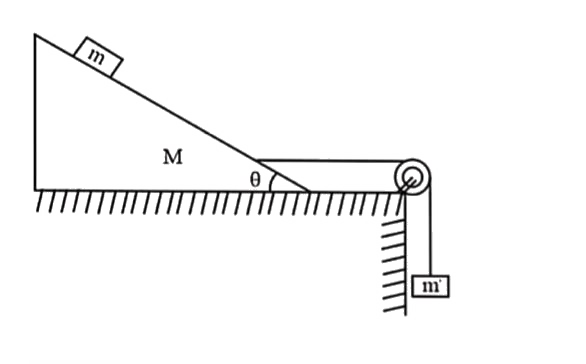
View SolutionFind the mass of the hanging block in which will prevent the smaller block of mass m from slipping over the triangular block of mass M. All the surfaces are frictionless and the strings and the pulleys are light

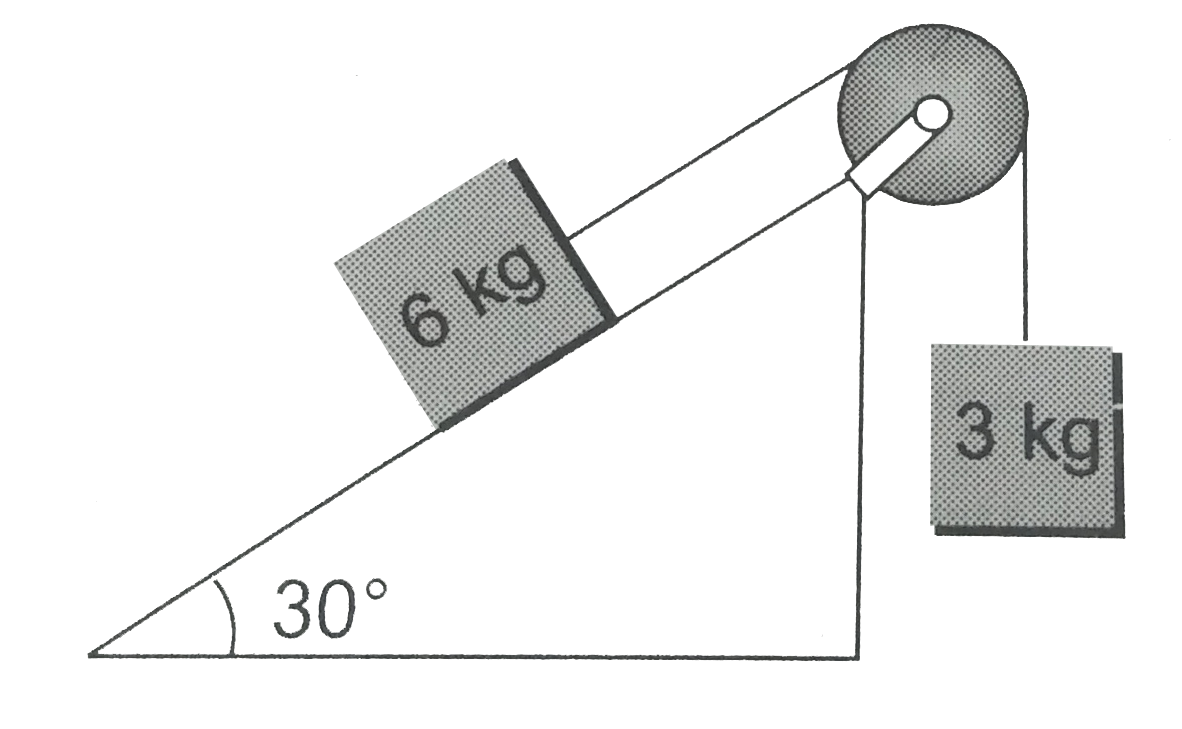
View SolutionTwo blocks of masses 3 kg and 6 kg are connected by a string as shown in the figure over a frictionless pulley. The acceleration of the system is
View SolutionThree blocks of masses m1,m2andm3 are connected by mass less string as shown kept on a frictionless table.

They are pulled with a force T3=40N. If m1=10kg,m2=6kgandm3=4kg, the tension T2 will be
View SolutionThree blocks of masses m1,m2andm3 are connected by a massless string as shown in figure on a frictionless table. They are pulled with a force T3=40N. If m1=10kg,m2=6kgandm3=4kg, then tension T2 will be

View Solution


