A block of mass "100kg" slides over a distance of "10m" on a horizontal surface.If the co-efficient of friction between the surfaces is "0.4" ,then the work done against friction (in "J" ) is:
4000
4200
3900
4500
To solve the problem, we need to calculate the work done against friction when a block of mass 100 kg slides over a distance of 10 m on a horizontal surface with a coefficient of friction of 0.4.
1. Identify the Given Values:
- Mass of the block, m=100kg
- Distance slid, d=10m
- Coefficient of friction, μ=0.4
2. Calculate the Normal Force (R):
- On a horizontal surface, the normal force R is equal to the weight of the block.
R=mg
- Where g (acceleration due to gravity) is approximately 10m/s2.
R=100kg×10m/s2=1000N
3. Calculate the Frictional Force (F_f):
- The frictional force can be calculated using the formula:
Ff=μR
- Substituting the values:
Ff=0.4×1000N=400N
4. Calculate the Work Done Against Friction (W):
- Work done against friction is given by the formula:
W=Ff×d
- Substituting the values:
W=400N×10m=4000J
5. Conclusion:
- The work done against friction is 4000J.
Final Answer:
The work done against friction is 4000 J.
---
- Mass of the block, m=100kg
- Distance slid, d=10m
- Coefficient of friction, μ=0.4
- On a horizontal surface, the normal force R is equal to the weight of the block.
R=mg
- Where g (acceleration due to gravity) is approximately 10m/s2.
R=100kg×10m/s2=1000N
- The frictional force can be calculated using the formula:
Ff=μR
- Substituting the values:
Ff=0.4×1000N=400N
- Work done against friction is given by the formula:
W=Ff×d
- Substituting the values:
W=400N×10m=4000J
- The work done against friction is 4000J.
The work done against friction is 4000 J.
Topper's Solved these Questions
Similar Questions
A block of mass m is kept over another block of mass 2m and the system rests on a smooth horizontal surface. The coefficient of friction between the block is 0.50. Find the work done by the force of friction on the smaller block by the bigger block during a displacement the of the system when a force mg is applied to the lower block
View SolutionA block of mass 1 kg lies on a horizontal surface in a truck. The coefficient of static friction between the block and the surface is 0.6. If the acceleration of the truck is 5m/s2, the frictional force acting on the block is…………newtons.
View Solution
Knowledge Check
A block of mass 50 kg slides over a horizontal distance of 1m. If the coefficient of friction between their surface is 0.2, then work done against friction is (take g=9.8m/s2) :
A98 JB72 JC56 JD34 JA block of mass 2 kg initially at rest moves under the action of an applied horizontal force of 6 N on a rough horizontal surface. The coefficient of friction between block and surface is 0.1. The work done by the applied force in 10 s is (Take g=10ms−2)
A200JB−200JC600 JD−600JA force F accelerates a block of mass m on horizontal surface. The coefficient of friction between the contact surface is . The acceleration of m will be -
AF−μmgMBzeroCmay be (A) or (B)DNone of these
A block of mass 10 kg is sliding on a surface inclined at 30∘ with horizontal . If coefficient of friction between the block and the surface is 0.5 , find acceleration produced in the block . Take g=9.8m/2 .
View SolutionA force of 10N is acting on a block of 20kg on horizontal surface with coefficient of friction μ=0.2. Calculate the work done by the force.
View SolutionThree blocks of masses 3 kg, 6 kg and 1 kg are connected by a string passing over two smooth pulleys attached at the two ends of the horizontal surface. If the co-efficient of friction between the block and the surface is 0.6, the frictional force acting on the block of mass 6 kg is
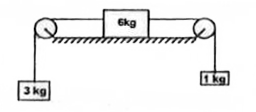
View SolutionA block of mass m is stationary on a horizontal surface. It is connected with a string which has no tension. The coefficient of friction between the block and surface is m . Then , the frictional force between the block and surface is:

View SolutionA block of mass M is being pulley along horizontal surface .The coefficient of friction the block and the surface is μ If another block of mass M/2 is placed on the block and it is pulled is again pulled on the surface , the coefficient of friction the block and the surface will be
View Solution
