A block of mass m is kept over another block of mass 2m and the system rests on a smooth horizontal surface. The coefficient of friction between the block is 0.50. Find the work done by the force of friction on the smaller block by the bigger block during a displacement the of the system when a force mg is applied to the lower block
mgd3
mgd
mgd2
zero
To solve the problem, we need to analyze the forces acting on the smaller block of mass m and determine the work done by the force of friction during the displacement D when a force mg is applied to the lower block of mass 2m.
1. Identify the Forces Acting on the Smaller Block:
- The weight of the smaller block is mg acting downwards.
- The normal force N exerted by the larger block (mass 2m) on the smaller block is equal to the weight of the smaller block, so N=mg.
- The force of friction f between the two blocks can be calculated using the formula:
\(
f = \mu N
\)
where \(\mu\) is the coefficient of friction (0.5 in this case).
2. Calculate the Force of Friction:
- Substituting the values we have:
\(
f = 0.5 \times mg = 0.5mg
\)
3. Determine the Displacement:
- When a force mg is applied to the lower block, the entire system (both blocks) will move together. The displacement of the smaller block relative to the larger block will be zero if the friction is sufficient to prevent slipping. Thus, during the displacement D, the smaller block moves with the larger block.
4. Calculate the Work Done by Friction:
- The work done by the force of friction on the smaller block during the displacement D is given by:
\(
W = f \cdot D
\)
- Substituting the value of the friction force:
\(
W = (0.5mg) \cdot D
\)
5. Final Expression for Work Done:
- Therefore, the work done by the force of friction on the smaller block during the displacement D is:
\(
W = 0.5mgD
\)
Summary of the Solution:
The work done by the force of friction on the smaller block during the displacement D when a force mg is applied to the lower block is \( W = 0.5mgD \).
- The weight of the smaller block is mg acting downwards.
- The normal force N exerted by the larger block (mass 2m) on the smaller block is equal to the weight of the smaller block, so N=mg.
- The force of friction f between the two blocks can be calculated using the formula:
\(
f = \mu N
\)
where \(\mu\) is the coefficient of friction (0.5 in this case).
- Substituting the values we have:
\(
f = 0.5 \times mg = 0.5mg
\)
- When a force mg is applied to the lower block, the entire system (both blocks) will move together. The displacement of the smaller block relative to the larger block will be zero if the friction is sufficient to prevent slipping. Thus, during the displacement D, the smaller block moves with the larger block.
- The work done by the force of friction on the smaller block during the displacement D is given by:
\(
W = f \cdot D
\)
- Substituting the value of the friction force:
\(
W = (0.5mg) \cdot D
\)
- Therefore, the work done by the force of friction on the smaller block during the displacement D is:
\(
W = 0.5mgD
\)
The work done by the force of friction on the smaller block during the displacement D when a force mg is applied to the lower block is \( W = 0.5mgD \).
Topper's Solved these Questions
Similar Questions
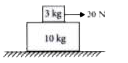
A 3kg block is placed over a 10kg block and both are placed on a smooth horizontal surface. The coefficient of friction between the blocks is 0.2. IF a horizontal force of 20N is applied to 3kg block. Find the acceleration of the two blocks.
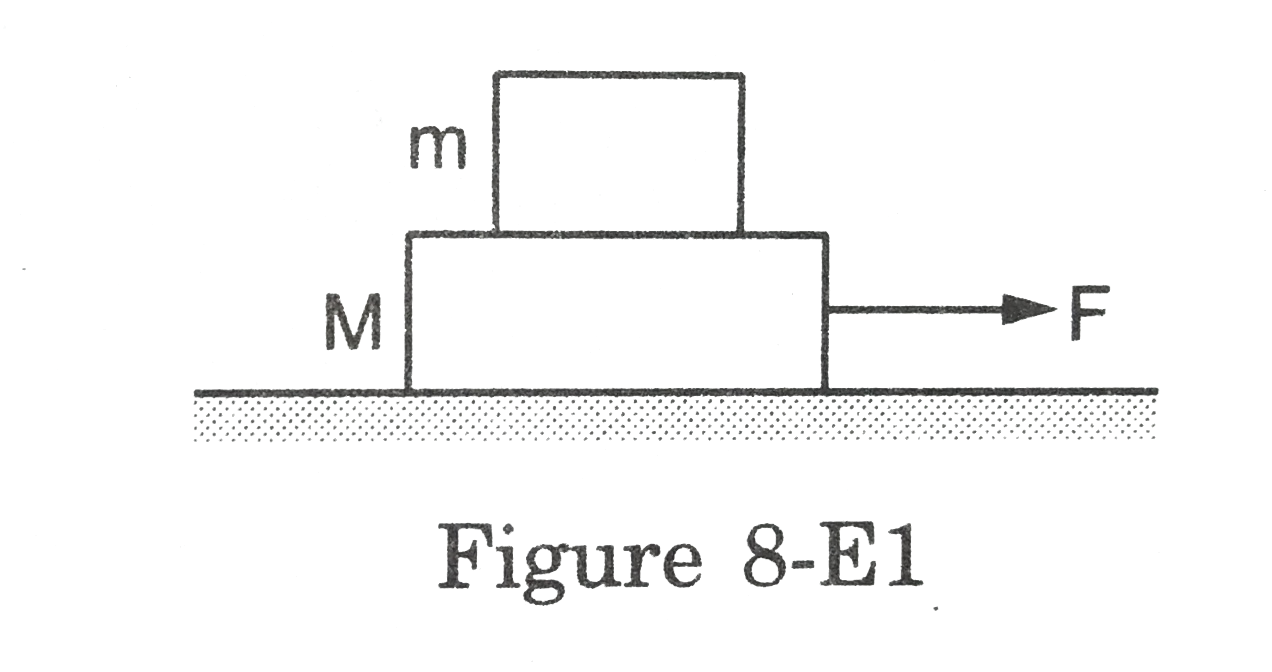
View SolutionA block of mass m is kept over another block of mass M nd the system rests on a horizontal force F acting on the lower block produces an accelertion F2(m+M) in the system the two blocks always move together. A. Find the coefficient of kinetic frictioin between the bigger block and th horizontal surface. b. find the frictional force acting on the smaller block. c. Find the work done by the force of friction on the smaller block by the bigger block during a displacement d of the system.
View Solution
Knowledge Check
A block of mass m is placed at rest on an inclination θ to the horizontal.If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
AmgBμmgcosθCmgsinθDμmgtanθA block is kept on a rough horizontal surface as shown. Its mass is 2 kg and coefficient of friction between block and surface (μ)=0.5. A horizontal force F is acting on the block. When
 AF = 4 N, acceleration is zero.BF = 4 N, friction is 10 N and acceleration is 3m/s2.CF = 14 N, acceleration is 2m/s2.DF = 14 N, friction is 14 N.
AF = 4 N, acceleration is zero.BF = 4 N, friction is 10 N and acceleration is 3m/s2.CF = 14 N, acceleration is 2m/s2.DF = 14 N, friction is 14 N.A force F accelerates a block of mass m on horizontal surface. The coefficient of friction between the contact surface is . The acceleration of m will be -
AF−μmgMBzeroCmay be (A) or (B)DNone of these
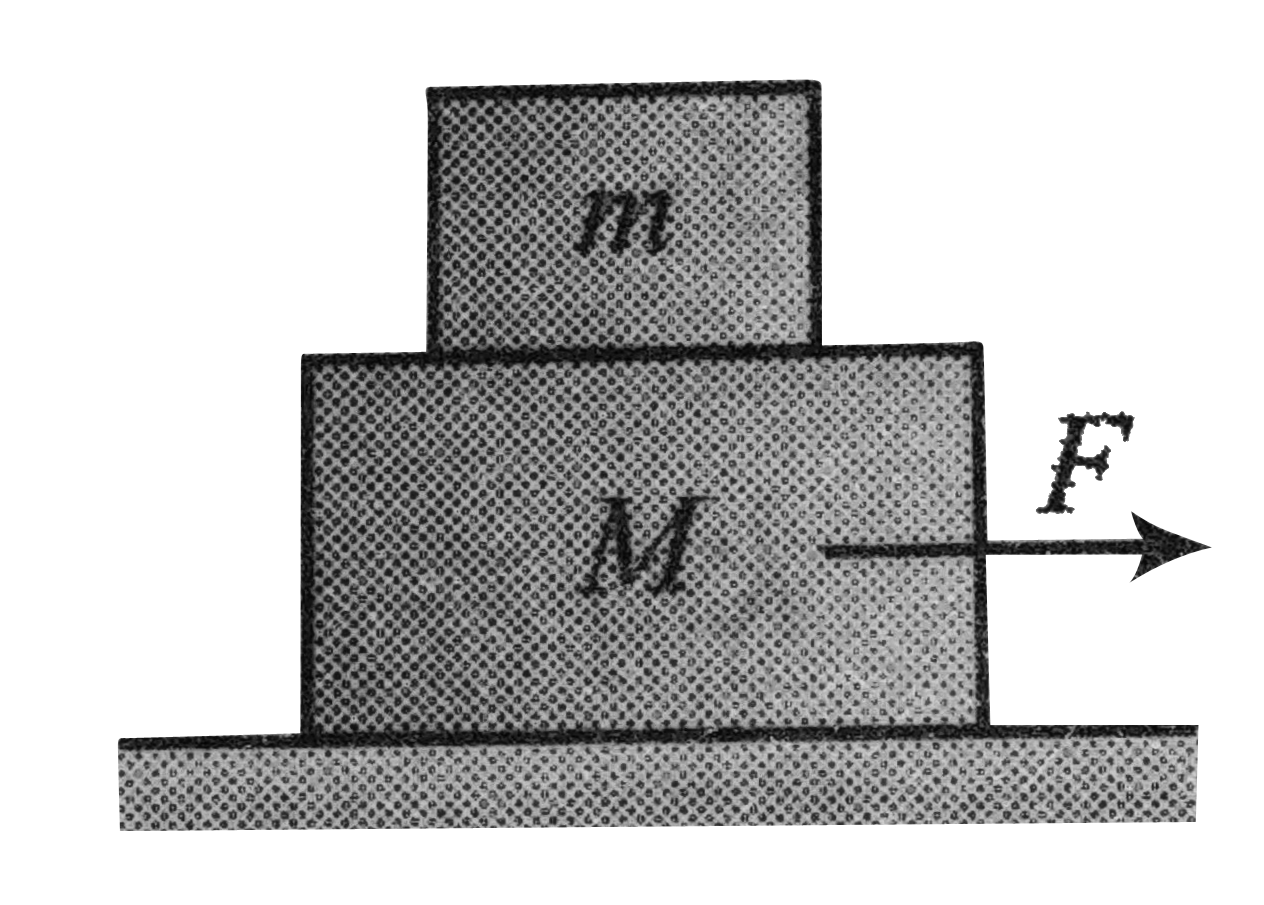
A block of mass m is kept over another block of mass M and the system rests on a horizontal surface. A constant horizontal force F acting on the lower block produces an acceleration F2(m+M) in the sytem. The two blocks always move together. Consider displacement d of the system.
a. Find the work done by friction on bigger block.
b. Find the coefficient of kinetic friction between the bigger block and the horizontal surface.
c. Find the frictional acting on the smaller block.
d. Find the work done by the force of friction on the smaller block by the bigger block.
e. Find the work done by static friction on bigger block.
View SolutionA small block of mass 20kg rests on a bigger block of mass 30kg, which lies on a smooth horizontal plane. Initially the whole system is at rest. The coefficient of friction between the blocks is 0.5. The horizontal force F=50N is applied on the lower block.
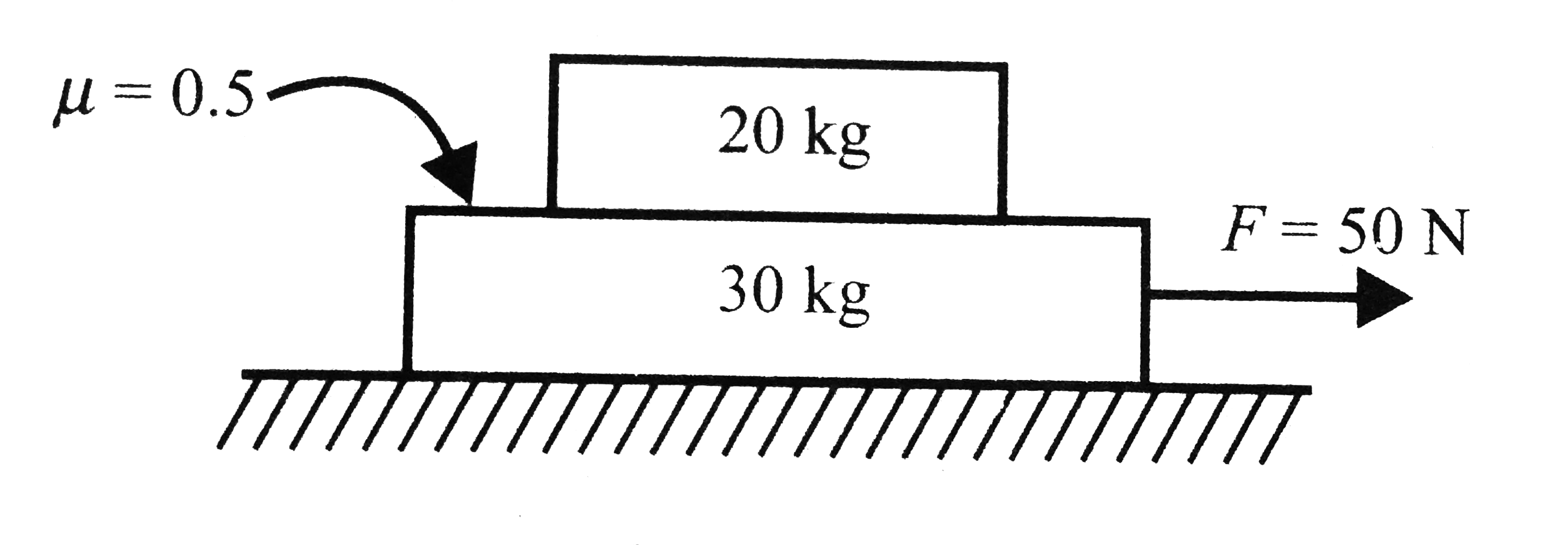
a. Find the work done by fricitonal force on upper block and on the lower block in t=2s.
b. Is the magnitude of work done by the frictional force on upper and lower blocks same?
c. Is the work done by the frictional force on the upper block converted to heat or mechanical energy or both?
View SolutionA block A of mass 2kg is placed over smooth block B of mass 4kg which is placed over a smooth horizontal floor The coefficient of friction between A and B is 0.4 when a horizontal forces of magnitude 10N is applied on A the acceleration of block of A and B are

View SolutionA block of mass m is pulled by a force of constant power P placed on a rough horizontal plane. The friction coefficient between the block and the surface is μ. Then
View SolutionA block of mass 4 kg is kept on a rough horizontal surface. The coefficient of static friction is 0.8. If a force of 19 N is applied on the block parallel to the floor, then the force of friction between the block and floor is
View Solution
