Three rotten apples are accidently mixed with fifteen good apples. Assuming the random variable "x" to be the number of rotten apples in a draw of two apples, the variance of "x" is
37153
47153
40153
57153
To find the variance of the random variable x, which represents the number of rotten apples drawn when selecting 2 apples from a total of 18 apples (3 rotten and 15 good), we will follow these steps:
Step 1: Identify Possible Values of x
The random variable x can take the following values:
- x=0: No rotten apples drawn.
- x=1: One rotten apple drawn.
- x=2: Two rotten apples drawn.
Step 2: Calculate Total Outcomes
The total number of ways to choose 2 apples from 18 is given by the combination formula:
Total outcomes=(182)=18×172=153
Step 3: Calculate Probabilities for Each Value of x
1. For x=0 (0 rotten apples):
- We choose 2 good apples from 15:
P(X=0)=(152)(182)=15×142153=105153
2. For x=1 (1 rotten apple):
- We choose 1 rotten apple from 3 and 1 good apple from 15:
P(X=1)=(31)⋅(151)(182)=3×15153=45153
3. For x=2 (2 rotten apples):
- We choose 2 rotten apples from 3:
P(X=2)=(32)(182)=3153
Step 4: Summarize Probabilities
Now we have:
- P(X=0)=105153
- P(X=1)=45153
- P(X=2)=3153
Step 5: Calculate the Mean μ
The mean μ is calculated as follows:
μ=∑(x⋅P(X=x))=0⋅105153+1⋅45153+2⋅3153
μ=0+45153+6153=51153=13
Step 6: Calculate E(X2)
Next, we calculate E(X2):
E(X2)=∑(x2⋅P(X=x))=02⋅105153+12⋅45153+22⋅3153
E(X2)=0+45153+12153=57153
Step 7: Calculate Variance σ2
The variance is given by:
σ2=E(X2)−μ2
Substituting the values:
σ2=57153−(13)2
=57153−19
To combine these fractions, convert 19 to have a common denominator of 153:
19=17153
Thus,
σ2=57153−17153=40153
Final Answer
The variance of x is:
40153
The random variable x can take the following values:
- x=0: No rotten apples drawn.
- x=1: One rotten apple drawn.
- x=2: Two rotten apples drawn.
The total number of ways to choose 2 apples from 18 is given by the combination formula:
Total outcomes=(182)=18×172=153
- We choose 2 good apples from 15:
P(X=0)=(152)(182)=15×142153=105153
- We choose 1 rotten apple from 3 and 1 good apple from 15:
P(X=1)=(31)⋅(151)(182)=3×15153=45153
- We choose 2 rotten apples from 3:
P(X=2)=(32)(182)=3153
Now we have:
- P(X=0)=105153
- P(X=1)=45153
- P(X=2)=3153
The mean μ is calculated as follows:
μ=∑(x⋅P(X=x))=0⋅105153+1⋅45153+2⋅3153
μ=0+45153+6153=51153=13
Next, we calculate E(X2):
E(X2)=∑(x2⋅P(X=x))=02⋅105153+12⋅45153+22⋅3153
E(X2)=0+45153+12153=57153
The variance is given by:
σ2=E(X2)−μ2
Substituting the values:
σ2=57153−(13)2
=57153−19
To combine these fractions, convert 19 to have a common denominator of 153:
19=17153
Thus,
σ2=57153−17153=40153
The variance of x is:
40153
Topper's Solved these Questions
Similar Questions
Four rotten oranges are accidentally mixed with 16 good ones. Three oranges are drawn at random from the mixed lot. Let X be the number of rotten oranges drawn. Find the mean and variance of X.
View SolutionFour bad oranges are mixed accidently with 16 good oranges. Find the probability distribution of the number of bad oranges in a draw of two oranges.
View Solution
Knowledge Check
An urn contains 4 white and 3 red balls. Let X be the number of red balls in a random draw of 3 balls . Find the mean and variance of X.
A57,2549B97,2449C127,2449DNone of these
An urn contains 4 white and 3 red balls. Let X be the number of red balls in a random draw of three balls. Find the mean and variance of X.
View SolutionAn urn contians 4 white and 3 red balls. Let X be the number of red balls in a random draw of 3 balls. Find the mean and variance of X.
View SolutionThe probability of selecting a rotten apple randomly from a heap of 900 apples is 0.18. What is the number of rotten apples in the heap?
View SolutionThe probability of selecting a rotten apple randomly from a heap of 900 apples is 0·18. What is the number of rotten apples in the heap ?
View SolutionOne-fourth of the apple are rotten.
View SolutionThe probablity distribution of a random variable X ,
the number of defects per 10 meters of a fabric is given by
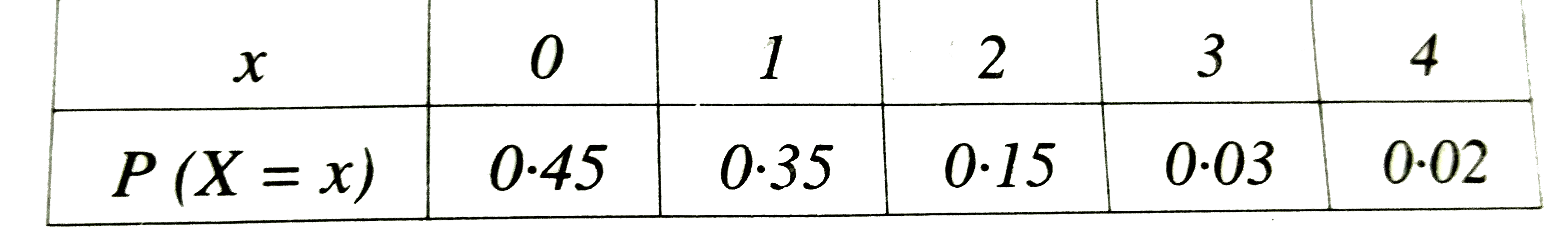
Find the variance of X .
View SolutionThe probability of selecting a rotten apple randomly from a heap of 900 apples is 0.18. What is the number of rotten apples in the heap?
View Solution
