√μ0/ε0 का मात्रक है:
न्यूटन/कुलाम
ओम
हेनरी
फैरड
The correct Answer is:B
μ0 का मात्रक न्यूटन/ऐम्पियर2 है तथा 1/ε0 का मात्रक न्यूटन-मीटर2//कुलाम^(2) है।
∴√μ0ε0 का मात्रक =
⎷न्यूटनऐम्पियर2×न्यूटन-मीटर2कुलाम2
=("न्यूटन-मीटर")/("ऐम्पियर-कुलाम")=("जूल"//"कुलाम")/("ऐम्पियर")=("वोल्ट")/("ऐम्पियर")="ओम"
Topper's Solved these Questions
- गतिमान आवेश तथा चुंबकीय क्षेत्र BOOK - NOOTAN HINDICHAPTER - गतिमान आवेश तथा चुंबकीय क्षेत्र EXERCISE - अतिलघु उत्तरीय
84 Videos
- गतिमान आवेश तथा चुंबकीय क्षेत्र BOOK - NOOTAN HINDICHAPTER - गतिमान आवेश तथा चुंबकीय क्षेत्र EXERCISE - लघु उत्तरीय
9 Videos
- गतिमान आवेश तथा चुंबकीय क्षेत्र BOOK - NOOTAN HINDICHAPTER - गतिमान आवेश तथा चुंबकीय क्षेत्र EXERCISE - वस्तुनिष्ठ प्रकार प्रश्न
39 Videos
- कॉलम का नियम तथा वैद्युत क्षेत्र BOOK - NOOTAN HINDICHAPTER - कॉलम का नियम तथा वैद्युत क्षेत्र EXERCISE - वस्तुनिष्ठ प्रकार प्रश्न
16 Videos
- चल कुण्डली धारामापी BOOK - NOOTAN HINDICHAPTER - चल कुण्डली धारामापी EXERCISE - वस्तुनिष्ठ प्रकार प्रश्न
15 Videos
Similar Questions
बायो - सेवर्ट का नियम लिखिए तथा इसकी सहायता से विधुत धारा के S.I. मात्रक को परिभाषित कीजिए ।
View Solutionधारावाही चालक के कारण उप्तन्न चुम्कीय क्षेत्र की तीव्रता से सम्बन्धित बाय-सेवर्ट नियम की व्यख्या कीजिए । बाय-सेवर्ट नियम के समीकरण की सहायता से निर्वात की चुंबकशीलता का मात्रक एवं विमीय समीकरण निकालिए।
View Solutionजैसे की चित्रित किया गया है। एक सम्मित तारे (symmetric star)के आकार के चालक में अपरिवर्तित धरा ी बह रही है। यहाँ विपरीत शीर्षों (diametrically opposoite vertices) के बीच की दुरी 4a है। चालक के केंद्र पर चुंबकीय क्षेत्र का मान होगा :
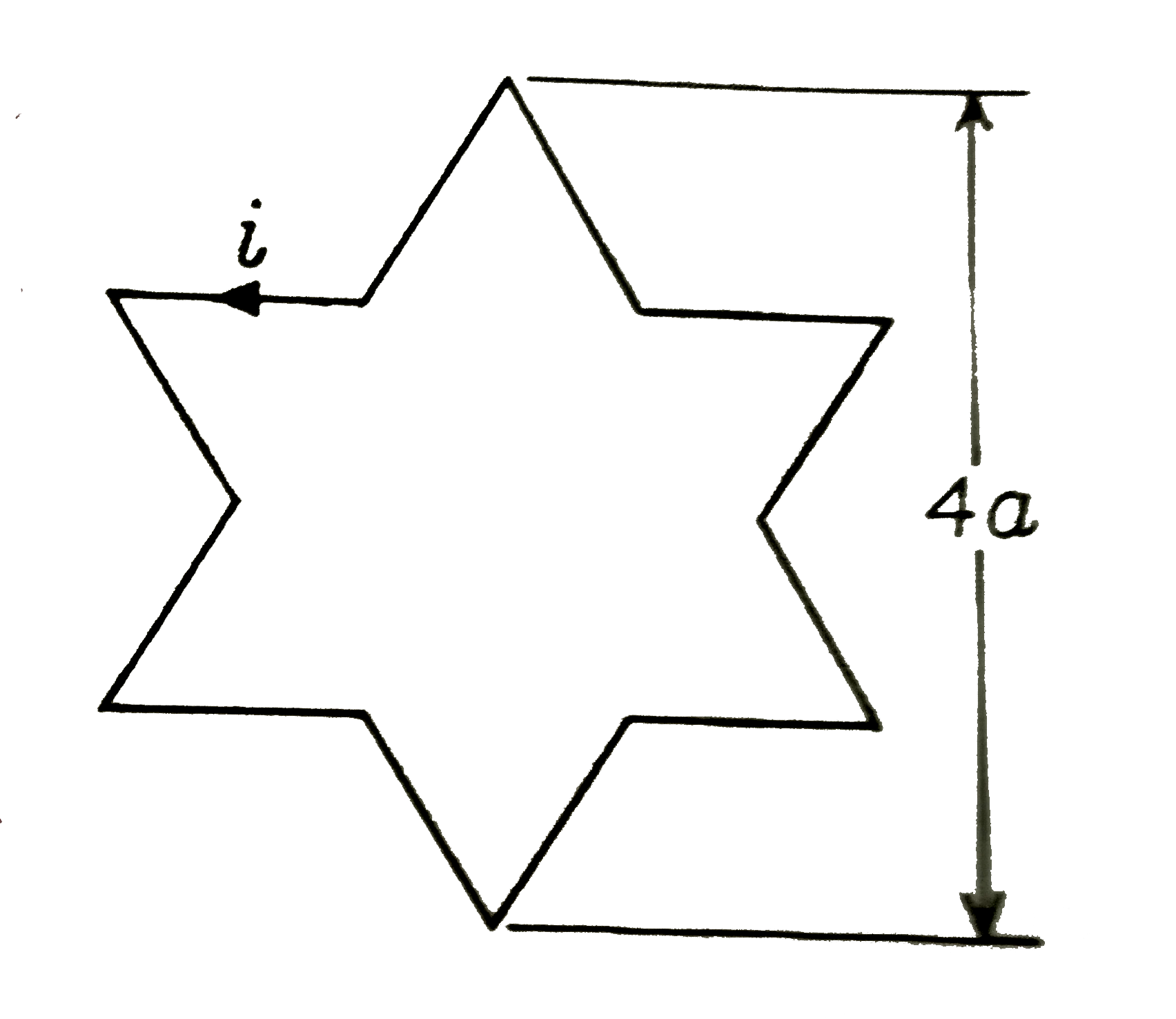
View Solutionकल्पना कीजिए कि एक प्रोटॉन और एक इलेक्ट्रॉन के आवेश में अल्प अंतर होता है। इनमे से एक −e है और दूसरा(e×Δe) है। यदि एक दूसरे से 'd' दूरी पर रखे हाइड्रोजन के दो परमाणुओं के बीच (जहाँ d परमाणु के साइज से बहुत अधिक है) स्थिर वैद्युत बल और गुरुत्वीय बल का परिणामी (नैट) शून्य है तो Δe कि कोटि होगी: (दिया है हाइड्रोजन का द्रव्यमान mh=1.67×10−27kg)
View Solutionआरेख में दण्ड (छड़) चुम्बको की व्यवस्थाओं के विन्यास दर्शाये गये है। प्रत्येक चुम्बक की द्विध्रुव आघूर्ण →M है। किस विन्यास में नेट चुम्बकीय द्विध्रुव आघूर्ण का मान अधिकतम होगा?

View Solutionε0μ0 का विमिये सूत्र लिखिए!
View Solution(μ0ε0)−1/2 का मान है -
View Solutionμ0ε0 का मान है-
View Solutionवैधुतशीलता (ε0) तथा (μ0) चुम्बकशीलता के माध्य में विद्युतचुंबकिय तरंग का वेग होगा :
View Solutionε0μ0 का विमीय सूत्र लिखिए।
View Solutionμ0ε0 का मान ज्ञात कीजिये। संकेतों के सामान्य अर्थ है।
View Solutionदिखाइये की √1√μ0ε0 की विमा वेग के समान है ।
View Solutionरिक्त स्थानों की पूर्ति करे।
ε0μ0 की विमाएँ (dimensions ) ……….. होती है।
View Solutionविधुत-चुंबकीय तरंग की संचरण चाल c के लिए प्रमाणित करे : c=1√ε0μ0, जहॉं ε0= निर्वात की परावैधुतता तथा a μ0= निर्वात की चुंबकशीलता।
View Solution1μ0ε0की विमाएँ है जहाँ संकतो के समान्य अर्थ है -
View SolutionThe dimensional formula μ0ε0 is
View Solution
