m द्रव्यमान का एक पिण्ड किसी आदर्श सिंप्रग के सिरे पर लटका हुआ सरल आवर्त दोलन करता है । सिंप्रग का बल-नियतांक k तथा पिण्ड का दोलनकाल T है । विमीय विधि से सिध्द कीजिए की समीकरण अशुध्द है । इसका सही रूप स्थापित कीजिए ।
यदि समीकरण सही है, तो इसके दोनों ओर के पदों की विमाये एक-सी होनी चाहिए । इसमें आयी राशियों के विमीय सूत्र अगर प्रकार है :
दोलनकाल T का विमीय सूत्र = [T], द्रव्यमान m का विमीय सूत्र = [M], बल-नियतांक k का विमीय सूत्र तथा की कोई विमा नहीं है । इस प्रकार उपरोक्त समीकरण में
बायीं ओर की विमाये = [T]
तथा दायी ओर की विमाये
चूँकि समीकरण के दोनों ओर की विमाये एक-सी नहीं है, अत: समीकरण अशुध्द है ।
समीकरण का सही रूप ज्ञात करने के लिए, मन की पिण्ड का दोलनकाल (T), द्रव्यमान (m) की a घात पर तथा बल-नियतांक (k) की b घात पर निर्भर करता है । तब
जहाँ K एक विमाहिन नियतांक है । दोनों ओर की विमाये लिखने पर
अथवा .
विमीय संतुलन के लिए, दोनों ओर के पदों की विमाये समान होनी चाहिए । अत:
a + b = 0 तथा -2b = 1.
हल करने पर : तथा
इन मानो को समीकरण (i) में रखने पर
प्रयोगो से प्राप्त परिणामो के आधार पर नियतांक
.
Topper's Solved these Questions
- विमीय विश्लेषण BOOK - NOOTAN HINDICHAPTER - विमीय विश्लेषण EXERCISE - वस्तुनिष्ठ प्रश्न
38 Videos
- विमीय विश्लेषण BOOK - NOOTAN HINDICHAPTER - विमीय विश्लेषण EXERCISE - अतिलघु उत्तरीय
16 Videos
- मात्रक, मापन तथा त्रुटि विश्लेषण BOOK - NOOTAN HINDICHAPTER - मात्रक, मापन तथा त्रुटि विश्लेषण EXERCISE - विविध प्रतियोगी परीक्षाओं के लिए (वस्तुनिष्ठ प्रकार प्रश्न)
19 Videos
- वृत्तीय गति BOOK - NOOTAN HINDICHAPTER - वृत्तीय गति EXERCISE - अतिरिक्त प्रशन
17 Videos
Similar Questions
विमीय सूत्र [ML2T−2] व्यक्त करता है :
View Solutionप्रकाश-वर्ष की विमा लिखिए ।
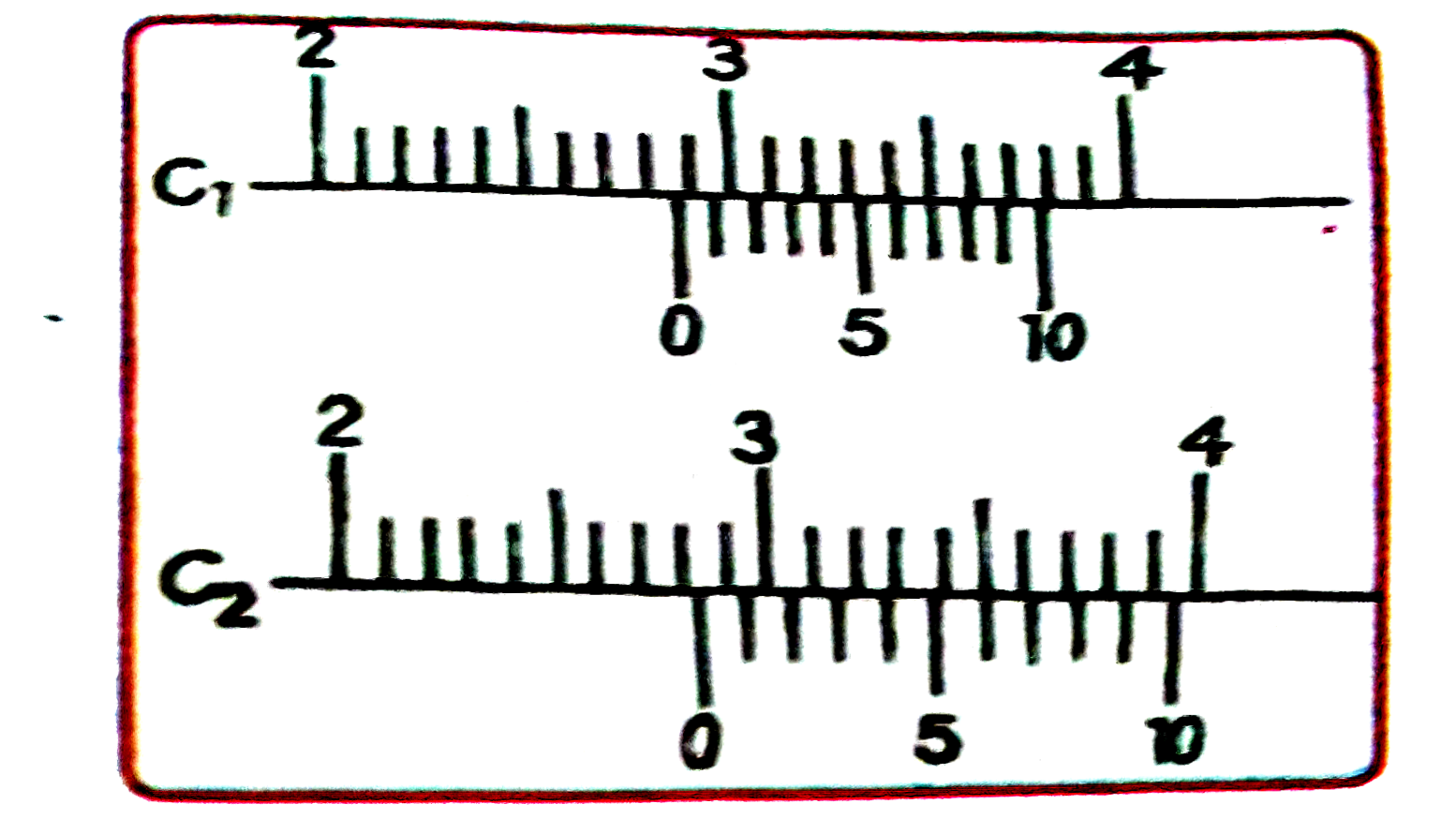
View Solutionदो वर्नियर कैलिपर्स इस तरह से हैं कि उनके मुख्य पैमाने का 1 समी, 10 समभागों में विभाजित है। एक कैलिपर (C1) के वर्नियर पमाने पर 10 बराबर भाग हैं जो कि मुख्य पैमा के 9 भागों के बराबर है। दूसरे कैलिपर (C2) के वर्नियर पैमाने पर भी 10 बराबर भाग हैं जो कि मुख्य पैमाने के 11 भागों के बराबर हैं। दोनों कैलिपर्स के पठनों को चित्र में दर्शाया गया है। C1 तथा C2 द्वारा मापे गए सही मान (सेमी में) क्रमश: हैं :
View Solutionचित्र में 0.04 kg सहती के किसी पिंड का स्थिति - समय ग्राफ दर्शाया जय है । इस गति के लिए कोई उचित भौतिक संदर्भ प्रस्तावित कीजिय। पिंड द्वारा प्राप्त दो क्रमिक आवेगों के बिच समय-अंतराल क्या है ? प्रत्येक आवेग का परिमाण क्या है ?

View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो रेखाओ x=−3 तथा x=5 से समान दूरी पर है ।
View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिंदु(1,2) से होकर जाती है जिसके द्वारा अक्षो से बने त्रिभुज का क्षेत्रफल 92 वर्ग इकाई है
View Solutionउस दीर्घवृत का समीकरण ज्ञात कीजिए जो बिन्दुओ (−3,1) और (2,−2) से होकर जाता है तथा जिसका केंद्र मूलबिंदु पर है । उत्केंद्रता भी ज्ञात कीजिए ।
View Solutionउस सरल रेखा का सदिश समीकरण ज्ञात कीजिए जो बिंदु (1, 2, 3) से गुजरती है तथा सदिश ˆi−2ˆj+3ˆk के समान्तर है | इसका कार्तीय रूप भी लिखिए |
View Solutionउन दो सरल रेखाओं के समीकरण ज्ञात कीजिए जो बिन्दु (0,a) से होकर जाती है तथा जिन पर बिन्दु (2a,2a) से खींचे गए लम्बो की माप a है।
View Solutionकिसी सरल रेखा से अक्षों के बीच काटे हुए अन्तः खण्ड का मध्य-बिन्दु (3,-2) है। रेखा का समीकरण ज्ञात कीजिए।
View Solutionएक परवलय के नाभिलम्ब का समीकरण x+y=8 तथा उसके शीर्ष पर स्पर्शी का समीकरण x+y=12 है, तो उसके नाभिलम्ब की लम्बाई है :
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिन्दु (a,b,c) से होकर जाती है तथा Y-अक्ष के समान्तरहै।
View Solutionएक समतल निर्देशाक्षों को क्रमश: A, B तथा C पर काटता है। यदि △ABC का केन्द्रक (2,-1, 3) है, तो समतल का समीकरण ज्ञात कीजिए।
View Solutionदोलन| सरल आवर्त गति का विस्थापन समीकरण
View Solutionदोलन|सरल आवर्त गति #!# सरल आवर्त गति का वेग समीकरण
View Solution
