यदि बल =αβ3+घनत्व, तब α तथा β की विमाये होंगी :
[ML−2T−2],[ML−1/3]
[M2L4T−2],[M1/3L−1]
[M2L−2T−2],[M1/3L−1]
[M2L−2T−2],[ML−3]
The correct Answer is:C
β3 की विमाये वही होंगी जो घनत्व की हैं । अर्थात, [ML−3], क्योंकि समान राशियाँ ही जोडी जा सकती हैं । अत: β की विमाये [M1/3L−2] हैं । α की विमाये वे होंगी जो बल × घनत्व की हैं अर्थात [MLT−2][ML−3]=[M2L−2^(−2)] विकल्प (c) सही है ।
Topper's Solved these Questions
- विमीय विश्लेषण BOOK - NOOTAN HINDICHAPTER - विमीय विश्लेषण EXERCISE - एन.सी.ई.आर.टी.प्रश्न
24 Videos
- विमीय विश्लेषण BOOK - NOOTAN HINDICHAPTER - विमीय विश्लेषण EXERCISE - अतिरिक्त प्रश्न
9 Videos
- विमीय विश्लेषण BOOK - NOOTAN HINDICHAPTER - विमीय विश्लेषण EXERCISE - आंकिक
10 Videos
- मात्रक, मापन तथा त्रुटि विश्लेषण BOOK - NOOTAN HINDICHAPTER - मात्रक, मापन तथा त्रुटि विश्लेषण EXERCISE - विविध प्रतियोगी परीक्षाओं के लिए (वस्तुनिष्ठ प्रकार प्रश्न)
19 Videos
- वृत्तीय गति BOOK - NOOTAN HINDICHAPTER - वृत्तीय गति EXERCISE - अतिरिक्त प्रशन
17 Videos
Similar Questions
रिक्त स्थान भरिए :
(a) किसी 1 cm भुजा वाले घन का आयतन ...................m3 के बराबर है ।
(b) किसी 2 cm त्रिज्या व 10 cm ऊँचाई वाले सिलिंडर का पृष्ठ क्षेत्रफल...............(mm)2 के बराबर है ।
(c) कोई गाड़ी 18 km/h की चाल से चल रही है तो यह 1 s में ..............m चलती है ।
(d) सीसे का आपेक्षिक घनत्व 11.3 है । इसका घनत्व .......... g cm−3 या ................. kg m−3 है ।
View Solutionवर्षा के समय में कोई व्यक्ति चाल v के साथ तेजी से चला जा रहा है । उसे अपने छाते को टेढ़ा करके उर्ध्व के साथ θ कोण बनाना पड़ता है । कोई विद्यार्थी कोण θ व v के बीच निम्नलिखित संबंध व्युतपन्न करता है :
tanθ=v,
और वह इस संबंध के औचित्य की सिमा पता लगाता है, जैसी की आशा की जाती है यदि v → 0 तो θ→0 | (हम यह मान रहे हैं की तेज हवा नहीं चल रही है और किसी खड़े व्यक्ति के लिए वर्षा उर्ध्वाधरत: पद रही है) । क्या आप सोचते हैं की यह संबंध सही हो सकता है ? यदि ऐसा नहीं है तो सही संबंध का अनुमान लगाइए ।
View Solutionवायु में ध्वनि कि चाल 332 मीटर/सेकण्ड है । यदि लम्बाई का मात्रक किमी तथा समय का मात्रक घण्टा हो, तब चाल का मान क्या होगा ?
View Solutionदो वर्नियर कैलिपर्स इस तरह से हैं कि उनके मुख्य पैमाने का 1 समी, 10 समभागों में विभाजित है। एक कैलिपर (C1) के वर्नियर पमाने पर 10 बराबर भाग हैं जो कि मुख्य पैमा के 9 भागों के बराबर है। दूसरे कैलिपर (C2) के वर्नियर पैमाने पर भी 10 बराबर भाग हैं जो कि मुख्य पैमाने के 11 भागों के बराबर हैं। दोनों कैलिपर्स के पठनों को चित्र में दर्शाया गया है। C1 तथा C2 द्वारा मापे गए सही मान (सेमी में) क्रमश: हैं :
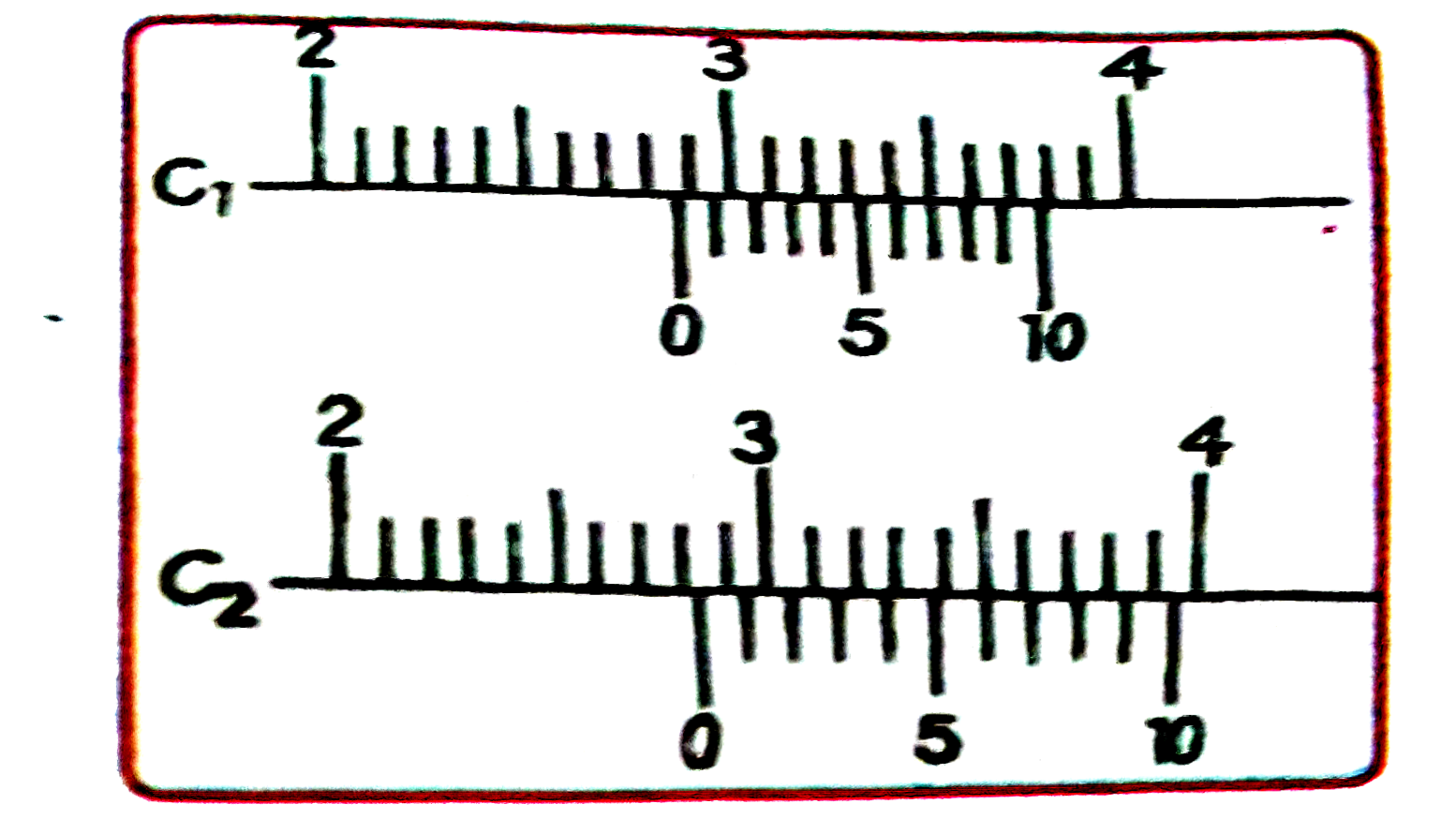
View Solutionचित्र में 0.04 kg सहती के किसी पिंड का स्थिति - समय ग्राफ दर्शाया जय है । इस गति के लिए कोई उचित भौतिक संदर्भ प्रस्तावित कीजिय। पिंड द्वारा प्राप्त दो क्रमिक आवेगों के बिच समय-अंतराल क्या है ? प्रत्येक आवेग का परिमाण क्या है ?

View SolutionIf α≠β and α2=5α−3andβ2=5β−3. find the equation whose roots are α/βandβ/α.
View SolutionIf alpha^(2)=5 alpha-3 beta^(2)=5 beta-3 then the value of (alpha)/(beta)+(beta)/(alpha) is
View SolutionTwo real numbers alpha and beta are such that alpha+beta=3 and | alpha-beta|=4 then alpha nad beta are the roots of the equation:
View SolutionIf alpha1=beta but alpha^(2)=2 alpha-3;beta^(2)=2 beta-3 then the equation whose roots are (alpha)/(beta) and (beta)/(alpha) is
View SolutionIf alpha!=beta but alpha^(2)=5 alpha-3,beta^(2)=5 beta-3, then find the equation whose roots are (alpha)/(beta) and (beta)/(alpha)
View Solutionयदि α≠β और α2=5α−3,β2=5β−3, तो समीकरण जिसके मूल αβ और βα हैं-
View Solutionयदि समीकरण ax2+bx+c=0 के मूल α व βहै तब αaβ+b+βaα+b बराबर है
View SolutionIf α≠β but α2=5α−3 and β2=5β−3 then the equation whose roots are αβ and βα is
View SolutionProve that ∣∣ ∣ ∣∣⎡⎢⎣αβγα2β2γ2α3β3γ3⎤⎥⎦∣∣ ∣ ∣∣=αβγ(α−β)(β−γ)(γ−α)
View SolutionWrite the formula: α3+β3=…………….a)(α+β)3−3αβ(α+β) b)(α−β)3+3αβ(α−β) c)(α+β)3−3αβ(α−β) d)(α−β)3−3αβ(α−β)
View Solution
