On the xy plane where O is the origin, given points, A(1,0), B(0,1) and C(1,1). Let P,Q, and R be moving points on the line OA, OB, OC respectively such that −−→OP=45t(−−→OA),−−→OQ=60t(−−→OB),−−→OR=(1−t)(−−→OC) with t>0. If the three points P,Q and R are collinear then the value of t is equal to
1106
7187
1100
none of these
The correct Answer is:B
Again it is given that the point P,Q and R are collinear
⇒−−→PQ=λ−−→QR
⇒15r(4→j−3→i)=λ[(1−t)(ˆi+ˆj)−60tˆj]
=λ[(1−t)ˆi+(1−6<ˆj)]
⇒45tt−1=4t1−61t
⇒3(1−61t)=4(t−1)
⇒3−183t=4t−4
⇒187t=7
⇒t=7187
Topper's Solved these Questions
Similar Questions
On the xy plane where O is the origin, given points, A(1,0),B(0,1)andC(1,1). Let P,Q,andR be moving points on the line OA,OB,OC respectively such that ¯¯¯¯¯¯OP=45t¯¯¯¯¯¯¯¯¯(OA),¯¯¯¯¯¯OQ=60t¯¯¯¯¯¯¯¯¯(OB),¯¯¯¯¯¯OR=(1−t)¯¯¯¯¯¯¯¯¯(OC) with t>0. If the three points P,QandR are collinear then the value of t is equal to
A 1106
B 7187
C 1100
D none of these
View SolutionOn the xy plane where O is the origin, given points, A(1,0),B(0,1)andC(1,1). Let P,Q,andR be moving points on the line OA,OB,OC respectively such that ¯¯¯¯¯¯OP=45t¯¯¯¯¯¯¯¯¯(OA),¯¯¯¯¯¯OQ=60t¯¯¯¯¯¯¯¯¯(OB),¯¯¯¯¯¯OR=(1−t)¯¯¯¯¯¯¯¯¯(OC) with t>0. If the three points P,QandR are collinear then the value of t is equal to
View Solution
Knowledge Check
Let O be the origin and P, Q, R be the points such that −−→PO+−−→OQ=−−→QO+−−→OR. Then which one of the following is correct?
AP, Q, R are the vertices of an equilateral triangleBP, Q, R are the vertices of an equilateral triangleCP, Q, R are collinearDNone of the aboveLet O be the origin nad P, Q, R be the points such that −−→PO+−−→OQ=−−→QO+−−→OR. Then which one of the following is correct?
AP, Q, R are the vertices of an equilateral triangleBP, Q, R are the vertices of an isosceles triangleCP, Q, R are collinearDNone of the above
If →PO+→OQ=→QO+→OR, show that the point, P,Q,R are collinear.
View SolutionIf D E and F be the mid ponts of the sides BC, CA and AB respectively of the △ABC and O be any point, then prove that −−→OA+−−→OB+−−→OC=−−→OD+−−→OE+−−→OF
View SolutionIf →PO+→OQ=→QO+→OR, show that the point, P,Q,R are collinear.
View SolutionIf O is the circumcentre and P the orthocentre of ΔABC, prove that −−→OA+−−→OB+−−→OC=−−→OP.
View SolutionGiven three points on the xy plane on O(0, 0), A(1, 0) and B(–1, 0). Point P is moving on the plane satisfying the condition (−−→PA.−−→PB)+(−−→OA.−−→OB)=0 . If the maximum and minimum values of ∣∣∣−−→PA∣∣∣∣∣∣−−→PB∣∣∣ are M and m respectively then find the value of are M and m respectively then the value of M2+m2.
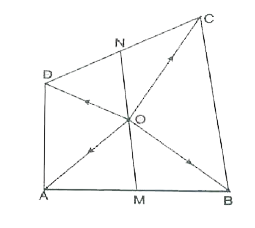
View SolutionIn the figure, M is the mid - point of [AB] and N is the mid - point of [CD] and O is the mid - point of [MN]. Prove that :
(i) −−→OA+−−→OB+−−→OC+−−→OD=→0
(ii) −−→BC+−−→AD=2−−−→MN.
View Solution
