The direction cosines of a line equally inclined to three mutually perpendiclar lines having direction cosines as l1,m1,n1,l2,m2,n2 and l3,m3,n3 are
l1+l2+l3,m1+m2+m3,n1+n2+n3
l1+l2+l3√3,m1+m2+m3√3,n1+n2+n3√3
l1+l2+l33,m1+m2+m33,n1+n2+n33
none of these
The correct Answer is:B
To find the direction cosines of a line that is equally inclined to three mutually perpendicular lines with given direction cosines, we can follow these steps:
Step 1: Understand the Direction Cosines
The direction cosines of a line are defined as the cosines of the angles that the line makes with the coordinate axes. For three mutually perpendicular lines, we denote their direction cosines as:
- Line 1: (l1,m1,n1)
- Line 2: (l2,m2,n2)
- Line 3: (l3,m3,n3)
Step 2: Use the Property of Mutually Perpendicular Lines
Since the lines are mutually perpendicular, the dot products of their direction cosines are zero:
1. l1l2+m1m2+n1n2=0
2. l2l3+m2m3+n2n3=0
3. l1l3+m1m3+n1n3=0
Step 3: Set Up the Equation for Equally Inclined Line
For a line that is equally inclined to these three lines, we need to find the direction cosines (l,m,n) such that:
l2+m2+n2=1
This ensures that the direction cosines form a unit vector.
Step 4: Express the Direction Cosines
Since the line is equally inclined to the three lines, we can express the direction cosines as:
l=l1+l2+l3√3,m=m1+m2+m3√3,n=n1+n2+n3√3
Step 5: Verify the Condition
We need to ensure that these values satisfy the condition l2+m2+n2=1:
(l1+l2+l3√3)2+(m1+m2+m3√3)2+(n1+n2+n3√3)2=1
This simplifies to:
(l1+l2+l3)2+(m1+m2+m3)2+(n1+n2+n3)23=1
Thus, we have:
(l1+l2+l3)2+(m1+m2+m3)2+(n1+n2+n3)2=3
Step 6: Final Direction Cosines
Thus, the direction cosines of the line that is equally inclined to the three mutually perpendicular lines are:
(l1+l2+l3√3,m1+m2+m3√3,n1+n2+n3√3)
The direction cosines of a line are defined as the cosines of the angles that the line makes with the coordinate axes. For three mutually perpendicular lines, we denote their direction cosines as:
- Line 1: (l1,m1,n1)
- Line 2: (l2,m2,n2)
- Line 3: (l3,m3,n3)
Since the lines are mutually perpendicular, the dot products of their direction cosines are zero:
1. l1l2+m1m2+n1n2=0
2. l2l3+m2m3+n2n3=0
3. l1l3+m1m3+n1n3=0
For a line that is equally inclined to these three lines, we need to find the direction cosines (l,m,n) such that:
l2+m2+n2=1
This ensures that the direction cosines form a unit vector.
Since the line is equally inclined to the three lines, we can express the direction cosines as:
l=l1+l2+l3√3,m=m1+m2+m3√3,n=n1+n2+n3√3
We need to ensure that these values satisfy the condition l2+m2+n2=1:
(l1+l2+l3√3)2+(m1+m2+m3√3)2+(n1+n2+n3√3)2=1
This simplifies to:
(l1+l2+l3)2+(m1+m2+m3)2+(n1+n2+n3)23=1
Thus, we have:
(l1+l2+l3)2+(m1+m2+m3)2+(n1+n2+n3)2=3
Thus, the direction cosines of the line that is equally inclined to the three mutually perpendicular lines are:
(l1+l2+l3√3,m1+m2+m3√3,n1+n2+n3√3)
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The direction cosines of a line equally inclines to three mutually perpendicular lines having D.C.'s
as (l1,m1,n1),(l2,m2,n2),(l3,m3,n3) areAthe direction cosines of three mutually perpendicular linesBthe direction ratios of three mutually perpendicular lines which are not direction cosines.Cthe direction cosines of three lines which need not be perpendicularDthe direction of three lines which need not be perpendicular - Question 2 - Select One
Two lines with direction cosines l1,m1,n1andl2,m2,n2 are at right angle of
Al1l2−m1m2−n1n2=0Bl1l2+m1m2+n1n2=0Cl2=l2,m1=m2,n1=n2Dl1l2=m1m2=n1n2 - Question 3 - Select One
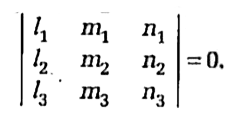
If l1,m1,n1,l2,m2,n2andl3,m3,n3 are direction cosines of three mutuallyy perpendicular lines then, the value of ∣∣ ∣∣l1m1n1l2m2n2l3m3n3∣∣ ∣∣ is
Al3m3n3B±1Cl1m1n1Dl2m2n2
The direction cosines of a line bisecting the angle between two perpendicular lines whose direction cosines are l1,m1,n1 and l2,m2,n2 are (1)l1+l22,m1+m22,n1+n22 (2)l1+l2,m1+m2,n1+n2 (3)l1+l2√2,m1−m22,n1+n2√2 (4)l1−l2,m1−m2,n1−n2 (5)n o n eo ft h e s e
View SolutionThe direction cosines of the lines bisecting the angle between the lines whose direction cosines are l1,m1,n1andl2,m2,n2 and the angle between these lines is θ, are
View SolutionIf three mutually perpendicular lines have direction cosines (l1,m1,n1),(l2,m2,n2)and(L3,m3,n3), then the line having direction cosines l1+l2+l3,m1+m2+m3,andn1+n2+n3, make an angle of
View SolutionThe direction cosines of the lines bisecting the angle between the lines whose direction cosines are I1,m1,n1andI2,m2,n2 and the angle between these lines is θ, are
View Solution(l1,m1,n1),(l2,m2,n2),(l3,m3,n3) are the direction cosines of three mutually perpendicular lines. If the line, whose direction ratios are l1+l2+l3,m1+m2+m3,n1+n2+n3, makes angle θ with any of these three lines, then cosθ is equal to
View Solution