The folloiwng figure shows the graph of a continuous function y = f(x) on the interval [1, 3]. The points A, B, C have coordinates (1,1), (3,2),(2,3), respectively , and the lines L1andL2 are parrallel, with L1 being tangent to the curve at C. If the area under the graph of y = f(x) from x = 1 to x = 3 is 4 square units, then the area of the shaded region is
![The folloiwng figure shows the graph of a continuous function y = f(x) on the interval [1, 3]. The points A, B, C have coordinates (1,1), (3,2),(2,3), respectively , and the lines L(1) and L(2) are parrallel, with L(1) being tangent to the curve at C. If the area under the graph of y = f(x) from x = 1 to x = 3 is 4 square units, then the area of the shaded region is](https://d10lpgp6xz60nq.cloudfront.net/physics_images/CEN_CAL_DPP_9_2_E01_501_Q01.png)
1
2
3
4
The correct Answer is:B
Equation of L2:y−1=2−13−1(x−1)
or 2y−2=x−1
2y−x=1
⇒ Slope of L2=1/2.
Equation of L1=y−3=12(x−2)
or 2y−x=4
∴ D(1,52)andE(3,72)
Area under f(x) = 4
∴ Shaded area = Area of trapezium DEFG - Area under f(x)
=12(52+72)×2−4
=6−4=2
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Comprehension Type
2 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Multiple Correct Answer Type
3 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Question Bank
29 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
20 Videos
Similar Questions
Knowledge Check
The following shows the graph of a continuous function y=f(x)on the interval [1,3]. The points A, B, C have coordinates (1,1),(3,2),(2,3) respectively, and the lines L1 and L2 are parallel, with L1 being tangent to the curve at C. If the area under the graph of y=f(x) from x=1 to x=3 is 4 square units, then the area of the shaded region is -
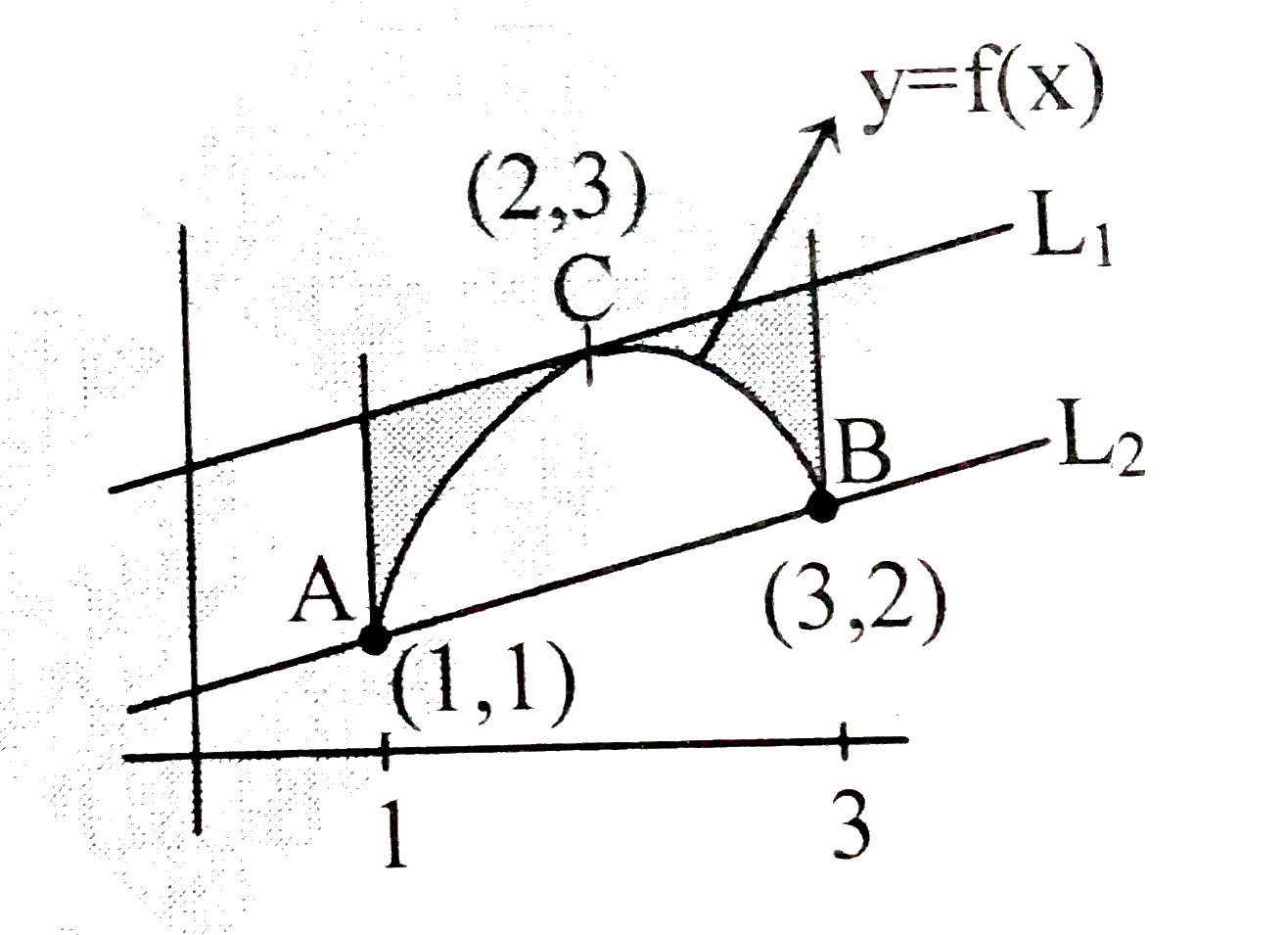A2B3C4D5
Coordinates of the point on the graph of the function f(x) = x−12−x where the tangent lines are perpendicular to the lines 8x + 2y = 1, are
View SolutionIf the graph of the function f(x)=ax−1xn(ax+1) is symmetrical about the y-axis ,then n equals (a)2 (b) 23 (c) 14 (d) 13
View SolutionA function y=f(x) has a second order derivative f(x)=6(x−1). If its graph passes through the point (2,1) and at that point the tangent to the graph is y=3x−5 then the function is
View SolutionA function y−f(x) has a second-order derivative fx=6(x−1). It its graph passes through the point (2,1) and at that point tangent to the graph is y=3x−5, then the value of f(0) is 1 (b) −1 (c) 2 (d) 0
View SolutionA function y=f(x) has a second-order derivative f''(x)=6(x−1). It its graph passes through the point (2,1) and at that point tangent to the graph is y=3x−5, then the value of f(0) is 1 (b) −1 (c) 2 (d) 0
View SolutionA function y=f(x) has a second order derivative f''(x)=6(x−1). If its graph passes through the point (2, 1) and at that point the tangent to the graph is y=3x−5, then the function is
View SolutionThe equation of line l1 is y=2x+3, and the equation of line l2 is y=2x-5.
View Solution