If graph of the function f(x) = $3 x^{4} + 2 x^{3} + a x^{2} - x + 2$ is concave upward for all real x, then find values of a,

Video Solution

Text Solution

Verified by Experts

We have f(x)= $12 {(x)}^{3} + 6 x^{2} + 2 a x - 1$
and $f (x) = 36 x^{2} + 12 x + 2 a$
Now graph of concave upward for all real x.
$∴ f (x) = 36^{2} + 12 x + 2 a > 0 \forall$ real x
Discriminant , $12^{2} - 4 (36) (2 a) < 0$
$\Rightarrow 1 - 2 a < 0$
$\Rightarrow a > 1 / 2$

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF DERIVATIVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Concavity and convexity :
if $f'' (x) > 0 \forall x \in (a, b)$ then the curve y=f(x) is concave up ( or convex down) in (a,b) and $if f'' (x) < 0 \forall x \in (a, b)$ then the curve y=f(x) is concave down (or convex up ) in (a,b)

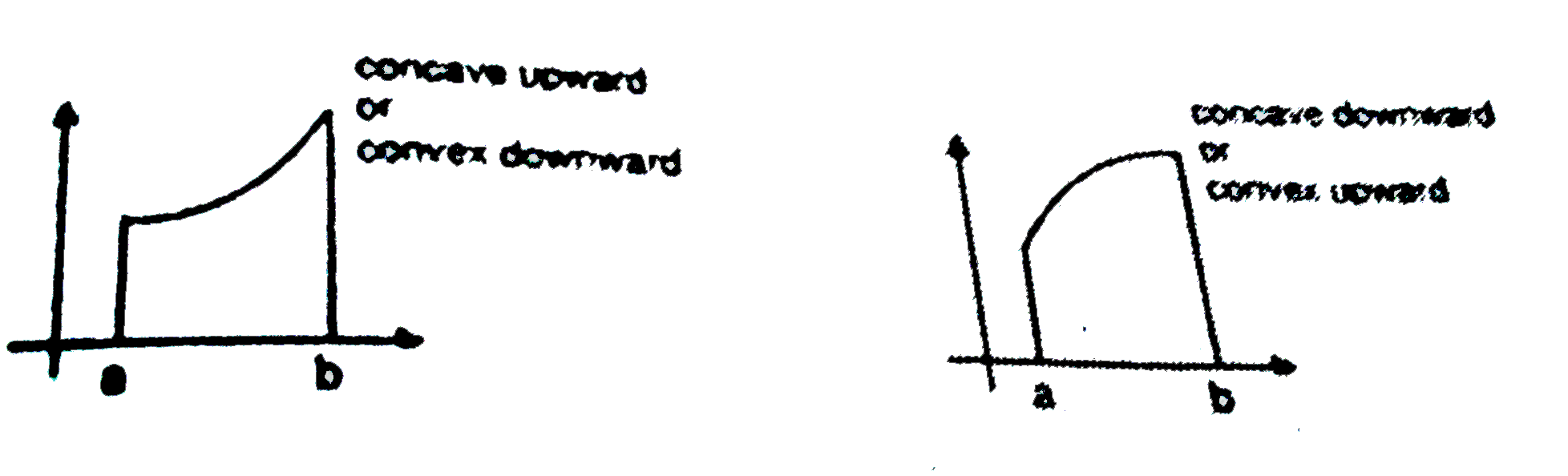
Inflection point :
The point where concavity of the curve changes is known as point of inflection (at inflection point $f'' (x)$ is equal to 0 or undefined)

Exhaustive set of values of 'a' for which the function $f (x) = x^{4} + a x^{3} + \frac{3 x^{2}}{2} + 1$ will be concave upward along the entire real line is :
A $[- 1, 1]$
B $[- 2, 2]$
C $[0, 2]$
D $[0, 4]$

CENGAGE-MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS-JEE Advanced Previous Year

Home
Ask Doubt
Profile