Doubtnut Promotions Sticky

The number of nonzero integral values of a for which the function f(x)=x4+ax3+3x22+1 is concave upward along the entire real line is___________

Video Solution
Doubtnut Promotions Banner
|
Answer

Step by step video & image solution for The number of nonzero integral values of a for which the function f(x)=x^4+a x^3+(3x^2)/2+1 is concave upward along the entire real line is___________ by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023
Class 12MATHSAPPLICATION OF DERIVATIVES

Similar Questions

Knowledge Check

  • Question 1 - Select One

    Concavity and convexity :
    if f''(x)>0∀x∈(a,b) then the curve y=f(x) is concave up ( or convex down) in (a,b) and iff''(x)<0∀x∈(a,b) then the curve y=f(x) is concave down (or convex up ) in (a,b)
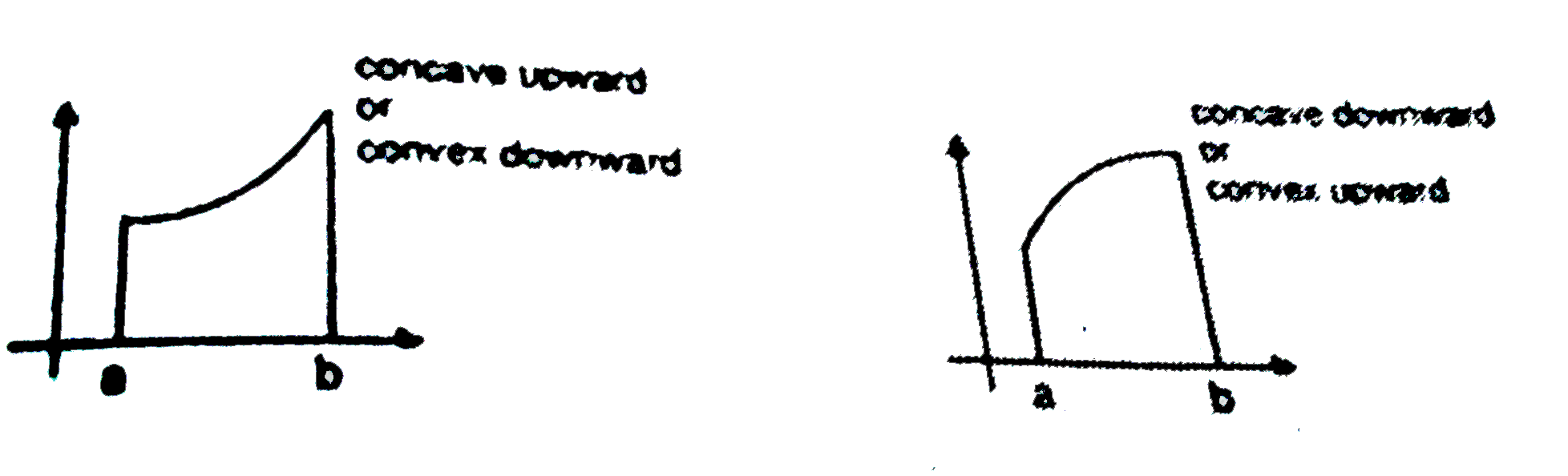
    ocr_image
    Inflection point :
    The point where concavity of the curve changes is known as point of inflection (at inflection point f''(x) is equal to 0 or undefined)
    ocr_image
    Exhaustive set of values of 'a' for which the function f(x)=x4+ax3+3x22+1 will be concave upward along the entire real line is :

    A[−1,1]
    B[−2,2]
    C[0,2]
    D[0,4]
  • Question 2 - Select One

    The number of integral values in the range of the function f(x)=sin−1x−cot−1x+x2+2x+6 is

    A10
    B11
    C12
    D8
  • Question 3 - Select One

    The interval into which the function y=x−1x2−3x+3 transforms the entire real line is

    A[1/3,2]
    B[−1/3,1]
    C[−1/3,2]
    Dnone of these