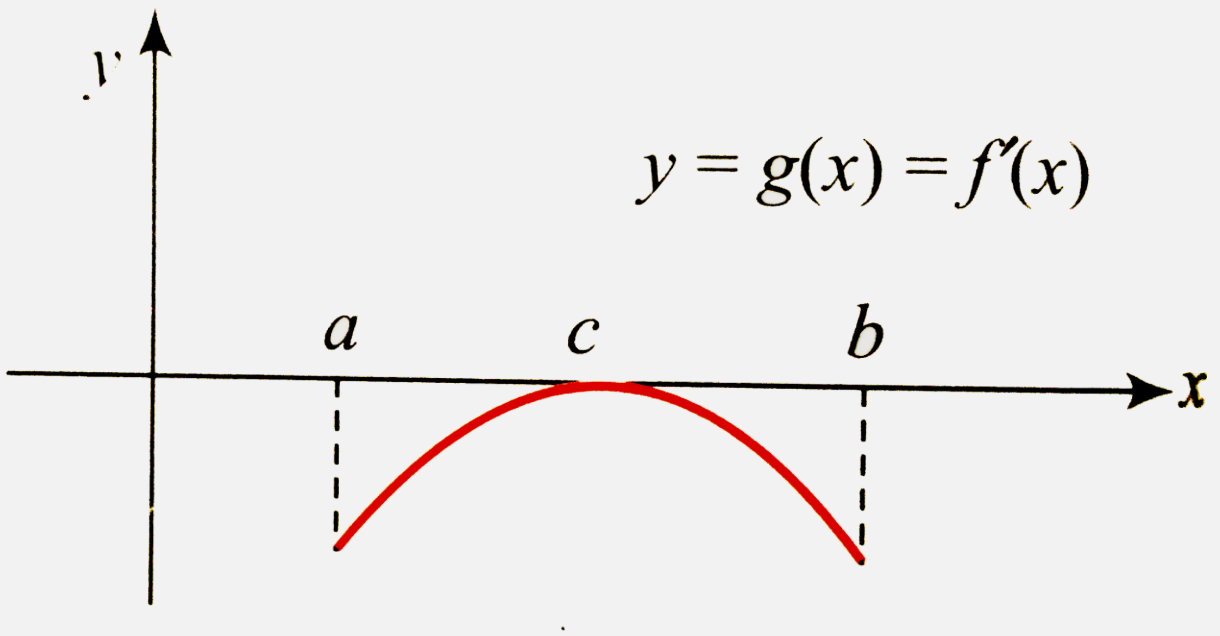
consider the graph of y=g(x)=f'(x) given that f(c ) =0, where y=f(x) is a polynomial funtion

The equation f(x)=0,a≤x≤b,has
four real roots
no real roots
two distinct real roots
at least three repeated roots
The correct Answer is:4
we note that f(c )=0 f(c )=0 also tangent to f(x) at x=c is y=0 so f(c )=0
Thus x =c is the repeated root of third order that is the equation f(x) =0 has at least three repeated roots
Topper's Solved these Questions
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGECHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Matrix Match Type
11 Videos
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGECHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Exercise (Numerical)
20 Videos
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGECHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Exercise (Comprehension)
42 Videos
- METHODS OF DIFFERETIATIONBOOK - CENGAGECHAPTER - METHODS OF DIFFERETIATIONEXERCISE - Question Bank
29 Videos
- MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSBOOK - CENGAGECHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type
6 Videos
Similar Questions
The graph of y=f(x) is given below
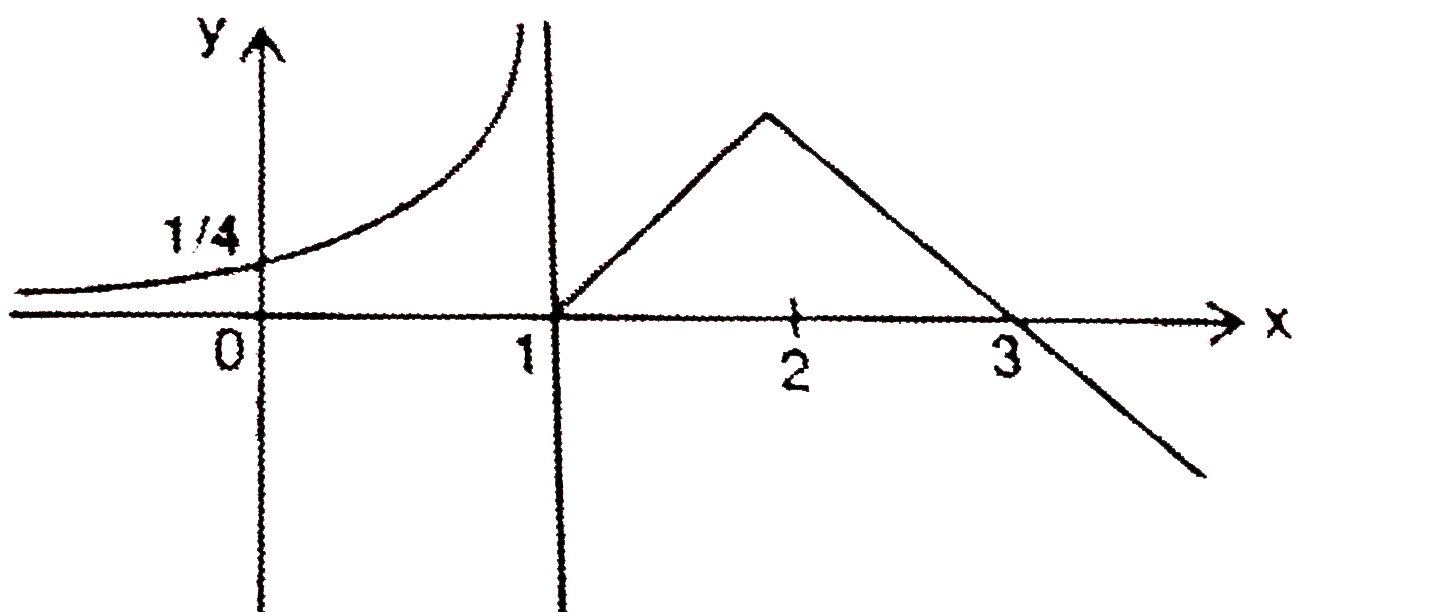
then the graph y=|f(|x|)| is :
View SolutionFollowing is the graph of y = f' (x) , given that f(c) = 0. Analyse the graph and answer the following questions.
(a) How many times the graph of y = f(x) will intersect the x - axis?
(b) Discuss the type of roots of the equation f (x) = 0, a≤x≤b.
(c) How many points of inflection the graph of y=f(x),a≤x≤b, has?
(d) Find the points of local maxima/minima ofy=f(x),a<xb.
(e) How many roots equation f''(x)=0 has?
View Solution
Knowledge Check
The graph of y=f(x) is given below

then the graph y=|f(|x|)| is :A B
B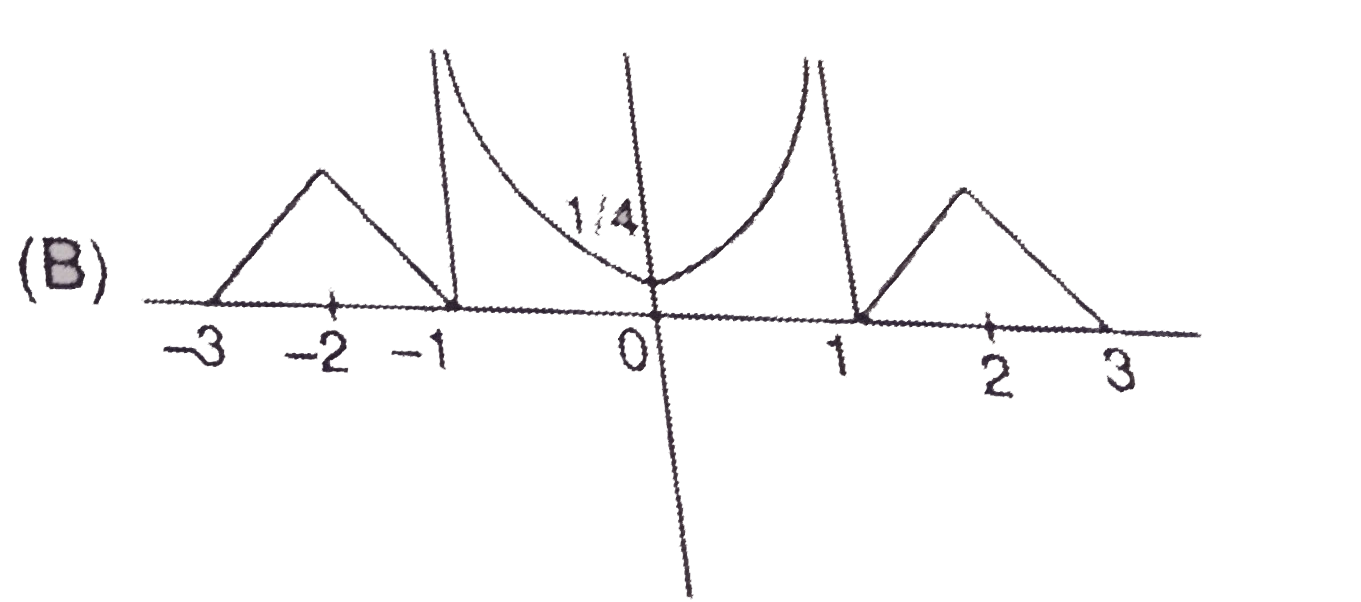 C
C Dnone of these
Dnone of these
Following is the graph of y = f' (x) , given that f(c) = 0. Analyse the graph and answer the following questions.
(a) How many times the graph of y = f(x) will intersect the x - axis?
(b) Discuss the type of roots of the equation f (x) = 0, a≤x≤b.
(c) How many points of inflection the graph of y=f(x),a≤x≤b, has?
(d) Find the points of local maxima/minima ofy=f(x),a<xb.
(e) How many roots equation f''(x)=0 has?

View SolutionFollowing is the graph of y = f(x).
<imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/CEN_GRA_C01_S01_005_Q01.pngwh=80%mx-autosty≤=background:white;><br>F∈dthes√oftheequation f(x) = 0, f(x) = 4 and f(x) = 10.
View SolutionFind the area of the region bounded by y=f(x),y=|g(x)| and the lines x=0,x=2, where f,g are continuous function satisfying f(x+y)=f(x)+f(y)−8xy,∀x,y∈R and g(x+y)=g(x)+g(y)+3xy(x+y),∀x,y∈R also , f'(0)=8andg'(0)=−4.
View SolutionFind the area of the region bounded by the curves y=f(x),y=|g(x)| and lines x=0,x=2, where f and g are continuous functions satisfying f(x+y)=f(x)+f(y)−8xy for all x,y∈R and g(x+y)=g(x)+g(y)+3xy(x+y) for all x,y∈R. Also f'(0)=8 and g\'(0)=-4.
View Solution(2x+3y5)+2f(x)+3f(y)5 and f′(0)=p and f(0)=q. Then f(0) is.
(where f(x) is a polynomial function)
View SolutionA real valued function f(x) satisfies the functional equation f(x−y)=f(x)f(y)−f(a−x)f(a+y), where a is a given constant and f(0)=1 , f(2a-x) =?
View SolutionGiven the graph of y=f(x).

Draw the graphs of the followin.
(a) y=f(1−x) (b) y=−2f(x)
(c) y=f(2x) (d) y=1−f(x)
View Solution
