consider the graph of y=g(x)=f'(x) given that f(c ) =0, where y=f(x) is a polynomial funtion

The graph of y =f(x),a≤x≤b has
A
two points of inflection
B
one point of inflection
C
no point of inflection
D
none of these
Text Solution
The correct Answer is:2
We have f(c )=0 the graph of y =f(x) has one point of inflection at x=c
|
Topper's Solved these Questions
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGECHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Matrix Match Type
11 Videos
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGECHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Exercise (Numerical)
20 Videos
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGECHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Exercise (Comprehension)
42 Videos
- METHODS OF DIFFERETIATIONBOOK - CENGAGECHAPTER - METHODS OF DIFFERETIATIONEXERCISE - Question Bank
29 Videos
- MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSBOOK - CENGAGECHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type
6 Videos
Similar Questions
Knowledge Check
The graph of y=f(x) is given below
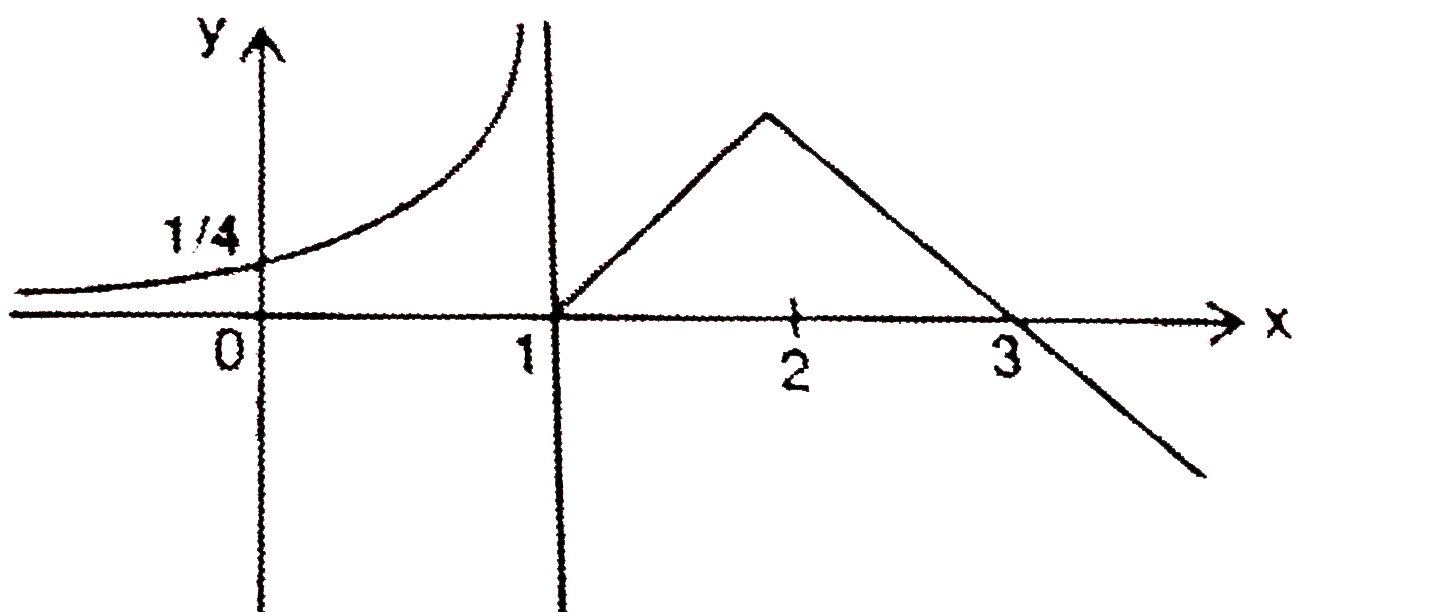
then the graph y=|f(|x|)| is :A B
B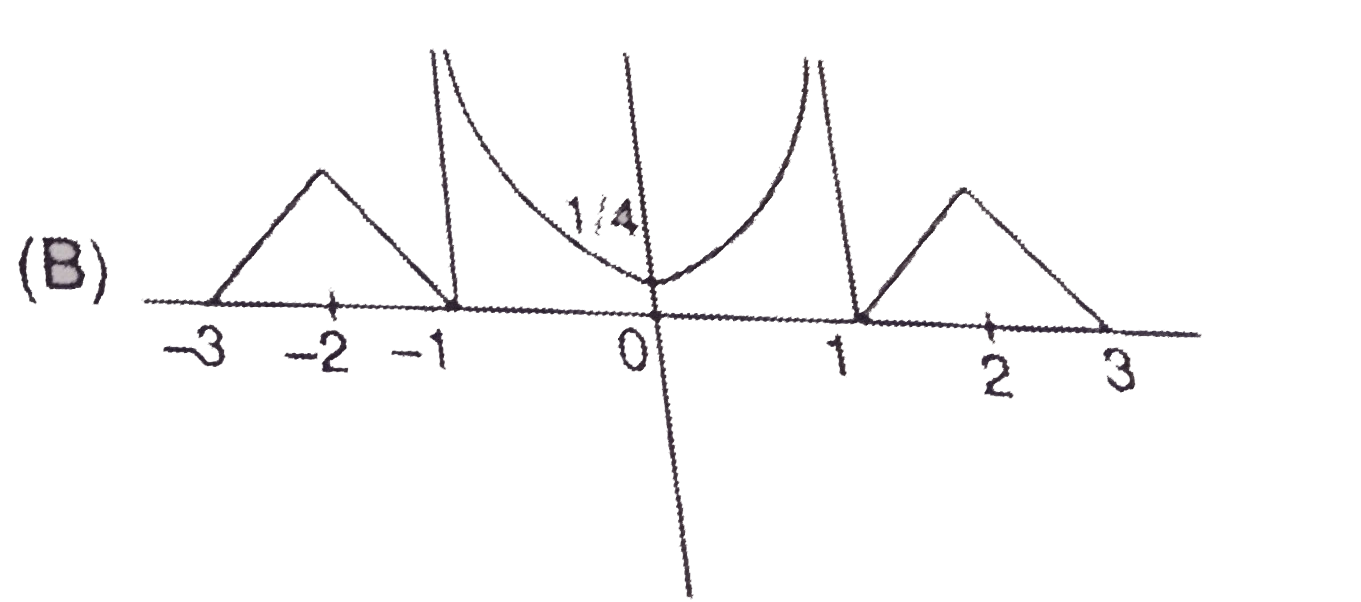 C
C Dnone of these
Dnone of these
Let graph of y=f(x) is
View SolutionLet graph of y=f(x) is
View SolutionGraph of y=f(x) is given, then
View SolutionThe graph of y=f(x) is given below

then the graph y=|f(|x|)| is :
View SolutionThe graph y = f (x) is as shown:
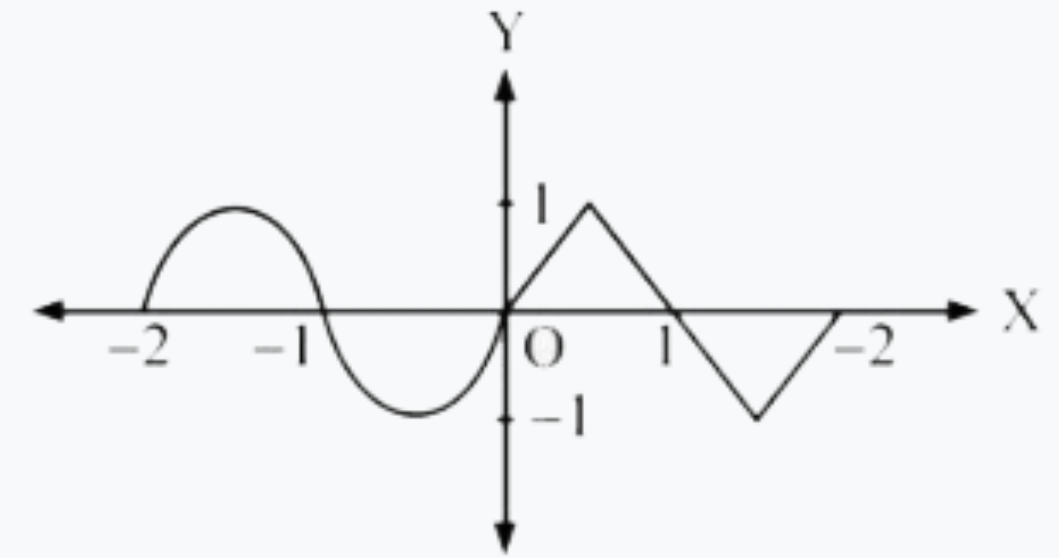
The graph of y = f (–|x|) is:
View SolutionThe graph y = f (x) is as shown:

The graph of y = f (–|x|) is:
View SolutionIf the graph of y=|f(x)| is as shown in figure
 then the graph of y=f(x) may be
then the graph of y=f(x) may be
View Solution


