A spring elongated by length 'L' when a mass 'M' is suspended to it. Now a tiny mass 'm' is attached and then released, its time period of oscillation is -
2π√(M+m)lMg
2π√mlMg
2π√L/g
2π√Ml(m+M)g
The correct Answer is:A
∵T=2π√MK ∴Mg=Kl
therefore T=2π√(M+m)lMg
Topper's Solved these Questions
- NEETBOOK - NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE)CHAPTER - NEETEXERCISE - PHYSICS
157 Videos
- NEETBOOK - NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE)CHAPTER - NEETEXERCISE - QUESTION
95 Videos
- MOTION IN TWO AND THREE DIMENSIONBOOK - NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE)CHAPTER - MOTION IN TWO AND THREE DIMENSIONEXERCISE - All Questions
47 Videos
- NEET 2020BOOK - NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE)CHAPTER - NEET 2020EXERCISE - All Questions
45 Videos
Similar Questions
Periodic time of oscillation T1 is obtained when a mass is suspended from a spring and if another spring is used with same mass then periodic time of oscillation is T2 . Now if this mass is suspended from series combination of above springs then calculated the time period.
View SolutionA spring of force constant 'k' is cut into four equal parts one part is attached with a mass m. The time period of oscillation will be
View Solution
Knowledge Check
A body of mass m is suspended from three springs as shown in figure. If mass m is displaced slightly then time period of oscillation is
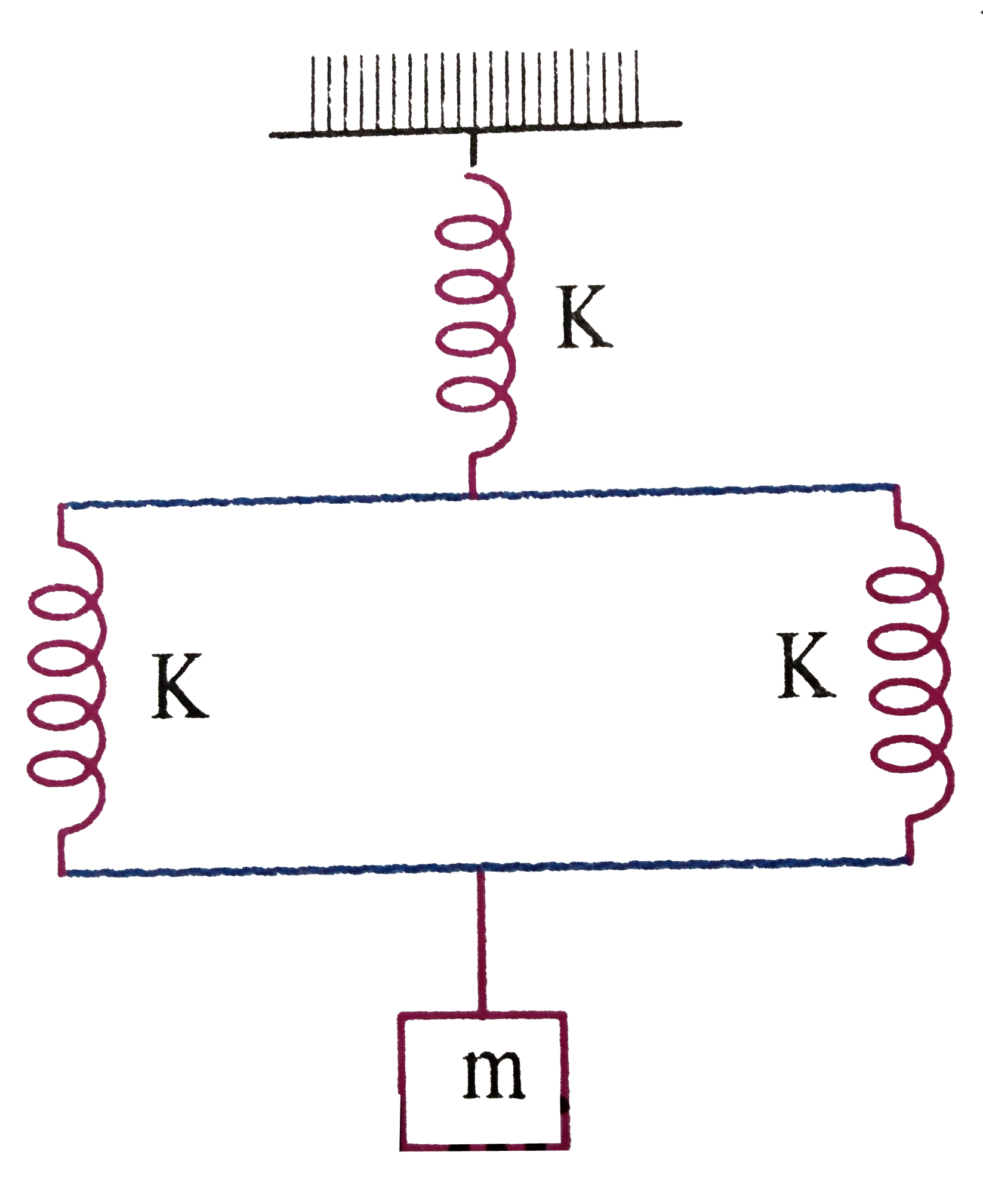 A2π√m3KB2π√3m2KC2π√2m3KD2π√3Km
A2π√m3KB2π√3m2KC2π√2m3KD2π√3KmA spring is stretched by 0.20 m , when a mass of 0.50 kg is suspended. When a mass of 0.25 kg is suspended, then its period of oscillation will be (g=10m/s2)
A0.328 secB0.628 secC0.137 secD1.00 secThe period of oscillation of a mass M, hanging from a spring of force constant k is T. When additional mass m is attached to the spring, the period of oscillation becomes 5T/4. m/M =
A9:16B25:16C25:9D16:9
Periodic time of oscillation T1 is obtained when a mass is suspended from a spring if another spring is used with same mass then periodic time of oscillation is T2. Now if this mass is suspended from series combination of above spring then calculate the time period.
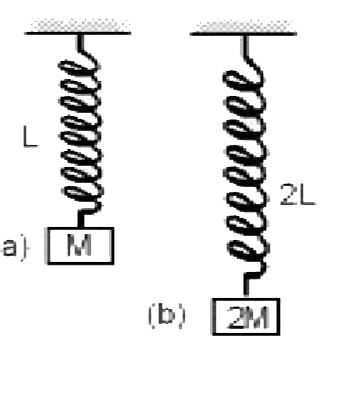
View SolutionTwo springs of the same material but of length L and 2L are suspended with masses M and 2M attached at their lower ends. Their time periods when they are allowed to oscillate will be in the ratio
View SolutionThe ratio of Young's modulus of two springs of same area of cross section and same length is 5 : 4 Equal masses are suspended from these springs. On stretching and then releasing, the springs start oscillating. Calculate the ratio of time period of oscillation.
View SolutionA particle of mass 'm' is attached to three identical springs A,B and C each of force constant 'K' as shown in figure. If the particle of mass 'm' is pushed slightly against the spring 'A' and released the period of oscillations is
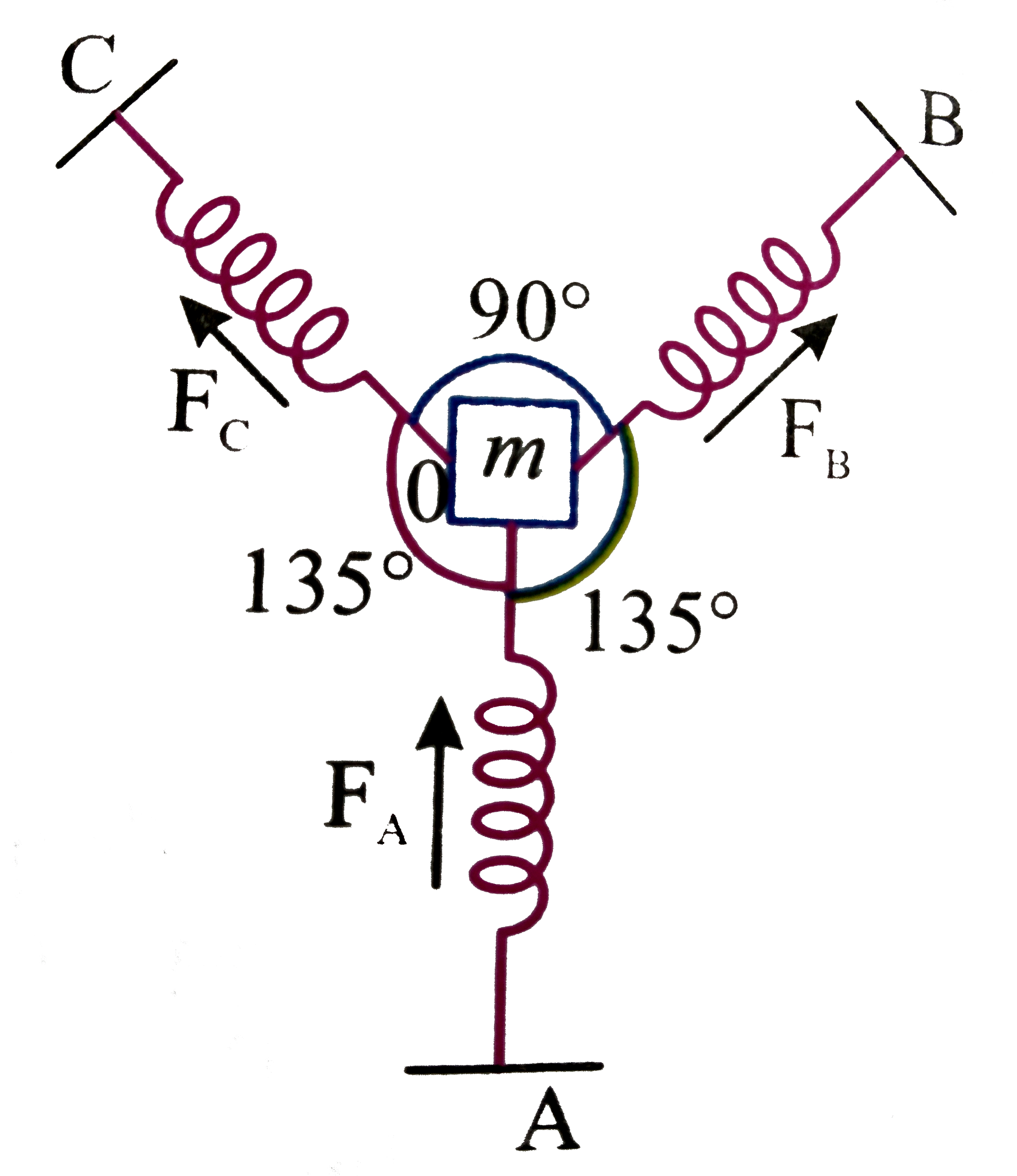
View SolutionThe period of oscilation of a mass M suspended a spring negligible mass is T if along with it and there mass M is also suspended the period of oscillation now be
View Solution