Two particles A and B are moving with the same velocity but wavelength of A is found to be double than that of B. What do you conclude ?
To solve the problem, we need to analyze the relationship between the wavelength and mass of two particles A and B that are moving with the same velocity.
1. Understand the relationship between wavelength and mass:
The de Broglie wavelength (λ) of a particle is given by the formula:
λ=hmv
where h is the Planck constant, m is the mass of the particle, and v is its velocity.
2. Given conditions:
- Both particles A and B are moving with the same velocity (v).
- The wavelength of particle A (λA) is double that of particle B (λB):
λA=2λB
3. Express the wavelengths in terms of mass:
For particle A:
λA=hmAv
For particle B:
λB=hmBv
4. Substituting the relationship of wavelengths:
Since λA=2λB, we can substitute:
hmAv=2(hmBv)
5. Simplifying the equation:
Canceling h and v from both sides (since they are constants and non-zero):
1mA=2⋅1mB
6. Rearranging the equation:
This implies:
mA=mB2
7. Conclusion:
From the above relationship, we conclude that the mass of particle A is half the mass of particle B:
mA=12mB
Final Conclusion:
Since the wavelength of particle A is double that of particle B, we conclude that particle A has a smaller mass compared to particle B, specifically, the mass of A is half that of B.
The de Broglie wavelength (λ) of a particle is given by the formula:
λ=hmv
where h is the Planck constant, m is the mass of the particle, and v is its velocity.
- Both particles A and B are moving with the same velocity (v).
- The wavelength of particle A (λA) is double that of particle B (λB):
λA=2λB
For particle A:
λA=hmAv
For particle B:
λB=hmBv
Since λA=2λB, we can substitute:
hmAv=2(hmBv)
Canceling h and v from both sides (since they are constants and non-zero):
1mA=2⋅1mB
This implies:
mA=mB2
From the above relationship, we conclude that the mass of particle A is half the mass of particle B:
mA=12mB
Since the wavelength of particle A is double that of particle B, we conclude that particle A has a smaller mass compared to particle B, specifically, the mass of A is half that of B.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - STRUCTURE OF ATOMEXERCISE - NCERT Questions And Exercises with Answers67videos
STRUCTURE OF ATOM
- BOOK - PRADEEPCHAPTER - STRUCTURE OF ATOMEXERCISE - NCERT Exemplar Problems With Answers, Hints and Solution (I. Multiple Choice Questions)16videos
STRUCTURE OF ATOM
- BOOK - PRADEEPCHAPTER - STRUCTURE OF ATOMEXERCISE - Test Your Grip (Fill in the Blanks)24videos
STRUCTURE OF ATOM
- BOOK - PRADEEPCHAPTER - STATES OF MATTER: SOLID MATTEREXERCISE - COMPETITION FOCUS (ASSERTION-REASON)17videos
STATES OF MATTER: SOLID MATTER
- BOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - MULTIPLE CHOICE QUESTION ( BASED ON PRACTICAL CHEMISTRY)3videos
THERMODYNAMICS
Similar Questions
Knowledge Check
- Question 1 - Select One
If particles are moving with same velocity, then maximum de - Broglie wavelength will be for
ANeutronBProtonCβ- particleDα - particle - Question 2 - Select One
Two identical balls 'A' and 'B' are moving with same velocity. If velocity of 'A' is reduced to half and of 'B' to zero, then the rise in temperature of 'A' to that is reduced to half and of 'B' to zero, then the rise in temperature of 'A' to that of 'B' is
A3:4B4:1C2:1D1:1 - Question 3 - Select One
Two objects A and B are moving with the same velocity. The mass of object A is twice that of B. The ratio of the kinetic energy of A to that B, (KA/KB) will be _______.
A4B2C1D12
A reaction proceeds with a uniform rate throughout. What do you conclude?
View SolutionThe observed spectrum of a star shows red shift. What do you conclude ?
View SolutionTwo particles AandB are moving with uniform velocity as shown in (Fig. 5.130) given below at t=0.
(a) Will the two particles collide ?
(b) Find out the shortest distance between two particles.
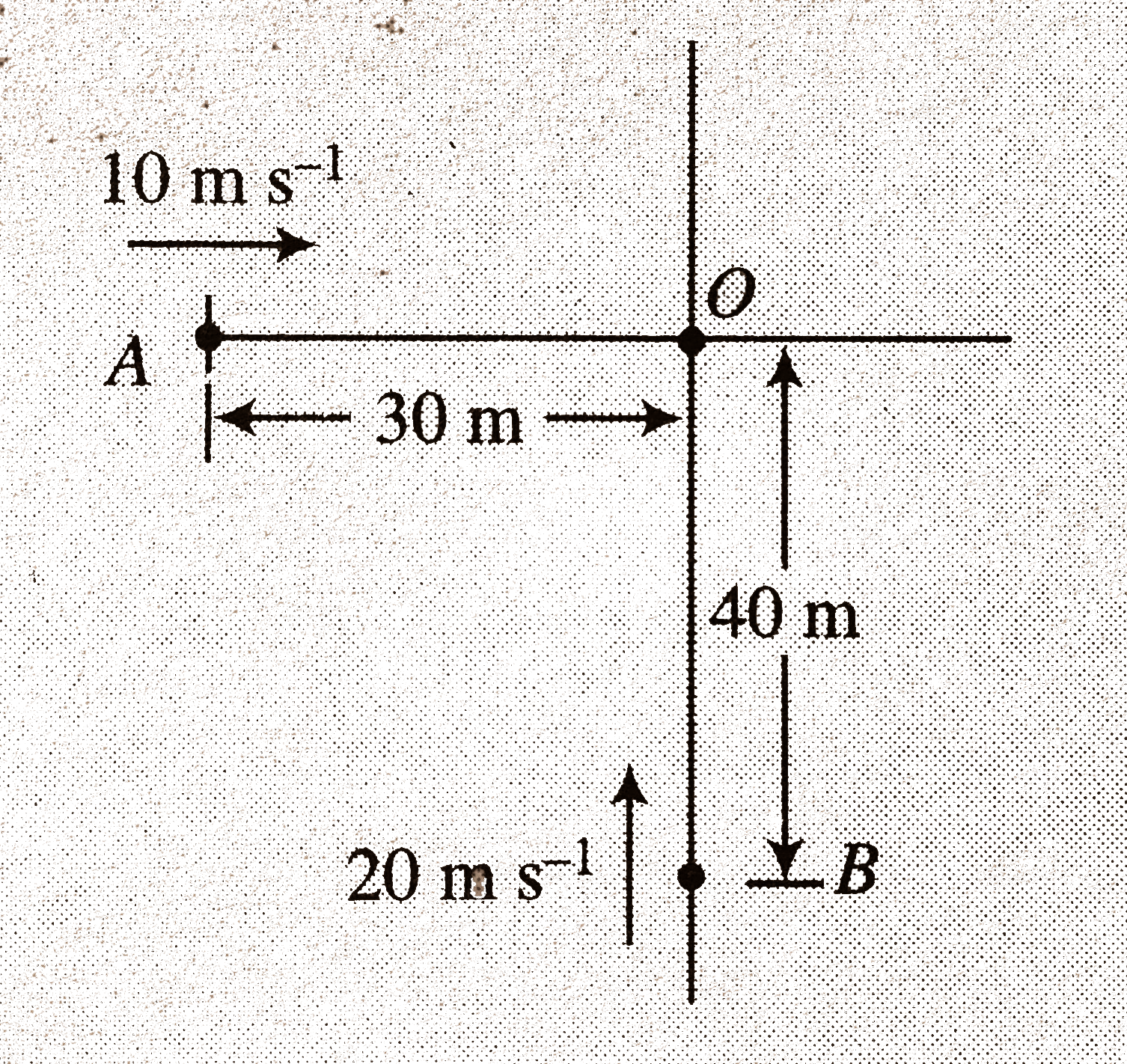 .View Solution
.View SolutionTwo particles A and B are in motion if wavelength of A is 5×10−8m, calculate wavelength of B so that its momentum is double of A
View SolutionTwo bod'ies A and B are moving with equal velocities. The mass of B is double that of A. In this context, which one of the following statements is correct?
View Solution

