An ideal gas in a thermally insulated vesselat internal pressure =P1, volume =V1and absolute temperature =T1 expands irreversibly against zero external pressure, as shoen in the diagram . The final internal pressure, volume and absolute temperature ofgas are P2,V2 and T2 respectively. For this expansion.
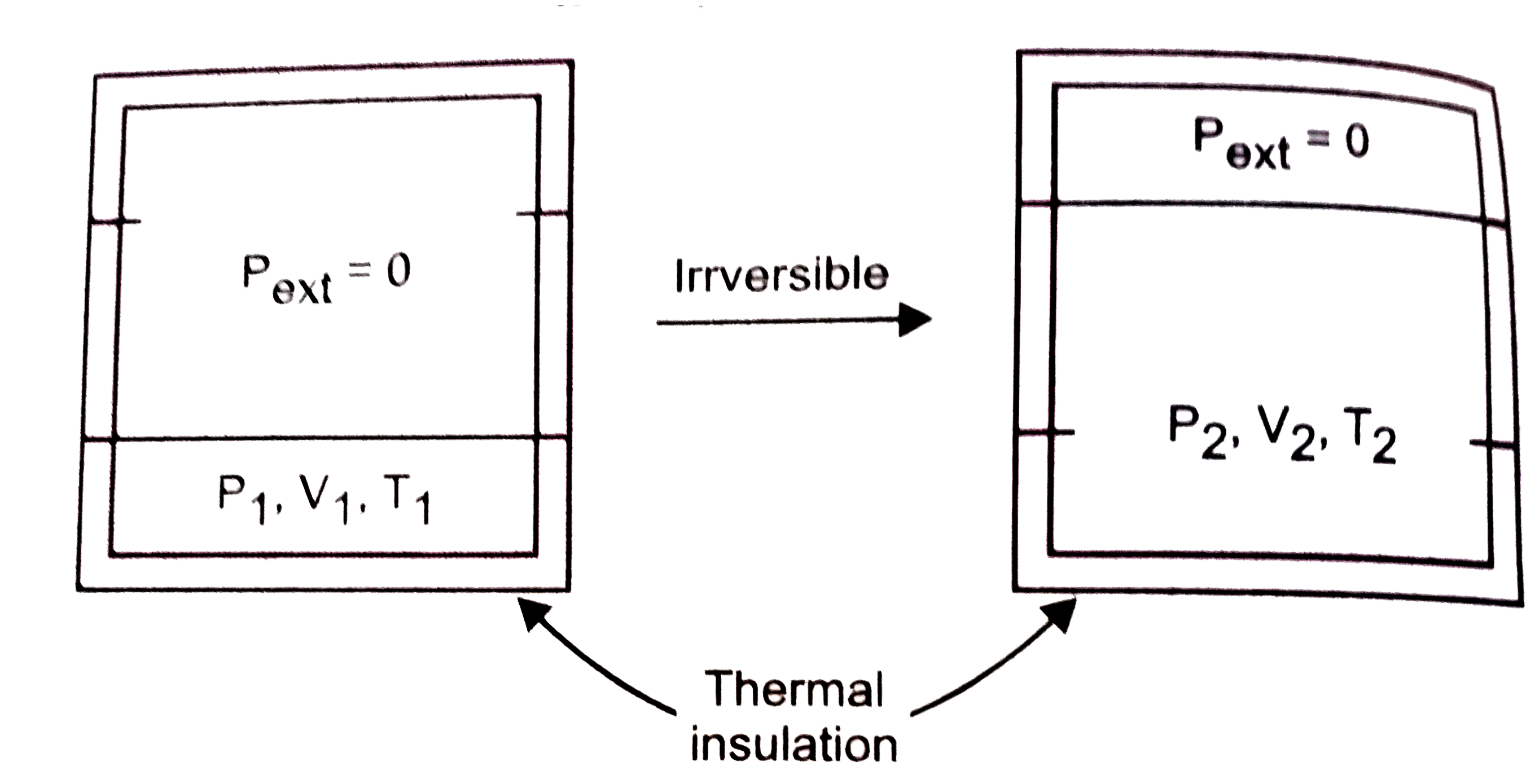
q=0
T2=T1
P2V2=P1V1
P2Vγ2=P1Vγ1
The correct Answer is:A, B, C
As the vessel is thermally insulated, the process is adiabatic and, therefore, q=0 Pext=0,therefore, w=0
From 1 st law of thermodynamics,ΔU=q+w
∴ΔU=0+0=0
But internal energy of an ideal gas isa function of temperature , therefore, ΔT=0,i.e.,T20=T1
Applying ideal gas equation PV=nRT P1V1=P2T2
Equation PVγ= constant is applicable only for an ideal gas in reversible adiabatic proces. Hence, P2Vγ2=P1Vγ1 isnot applicable.
Topper's Solved these Questions
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Comprehension 1
1 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Comprehension 2
2 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - SHORT ANSWER QUESTIONS
65 Videos
- STRUCTURE OF ATOMBOOK - PRADEEPCHAPTER - STRUCTURE OF ATOMEXERCISE - Competition Focus (JEE (Main and Advanced)/Medical Entrance (IX. Assertion And Reason Type Questions (Type II))
12 Videos
Similar Questions
An ideal gas in a thermally insulated vessel at internal pressure =P1, volume =V1 and absolute temperature =T1 expands irreversibly against zero external pressure, as shown in the diagram. The final internal pressure, volume and absolute temperature of the gas are P2,V2 and T2 respectively. For this expansion.
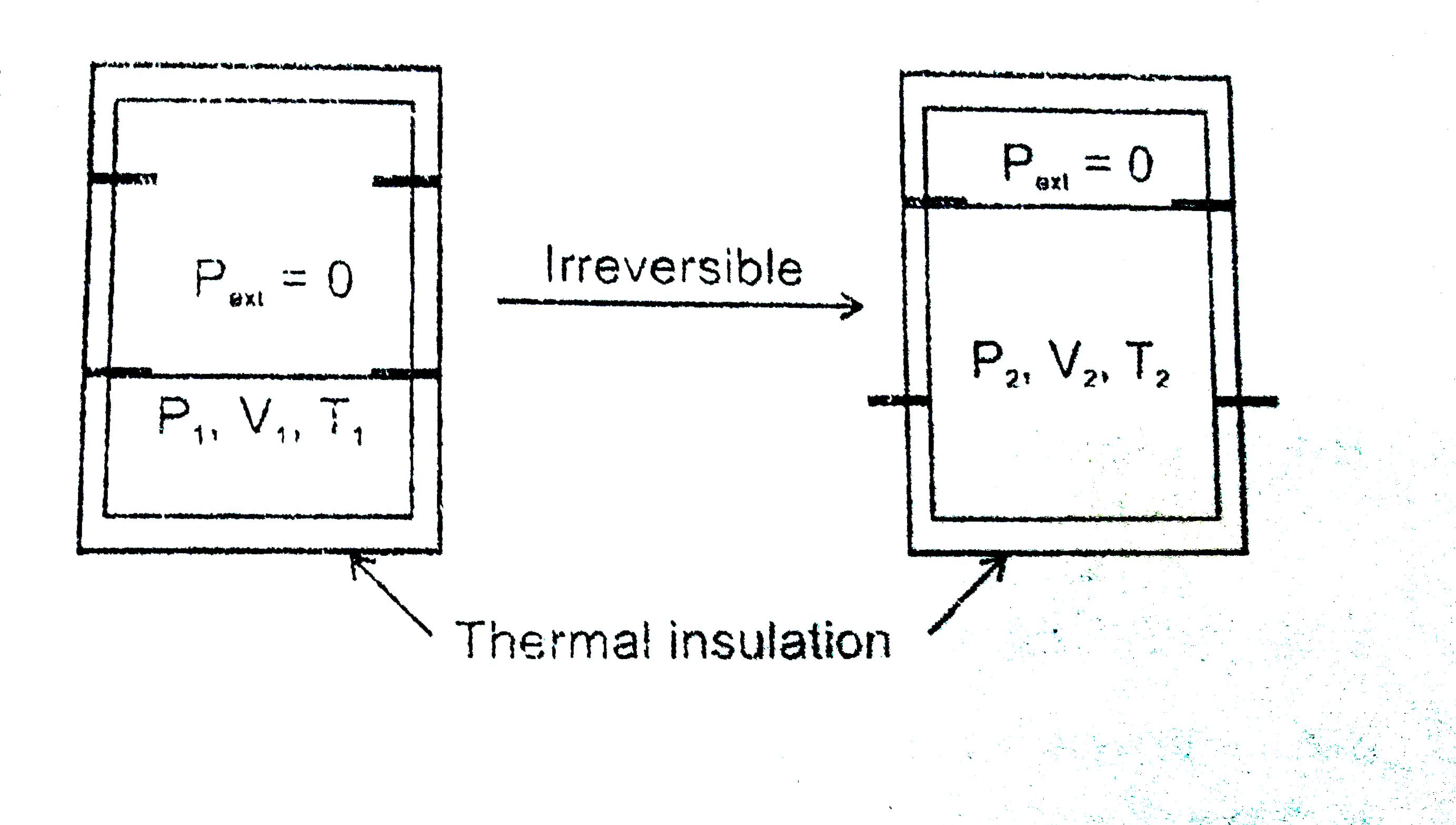
View SolutionAn ideal gas in a thermally insulated vessel at internal pressure = P1, volume =V1 and absolute temperature =T1 expands irreversibly against zero external pressure, as shown in the diagram. The final internal pressure, volume and absolute temperature of the gas are P2,V2andT2, respectively. For this expansion.
View Solution
Knowledge Check
An ideal gas in a thermally insulated vessel at internal pressure =P1, volume =V1 and absolute temperature =T1 expands irreversibly against zero external pressure, as shown in the diagram. The final internal pressure, volume and absolute temperature of the gas are P2,V2 and T2 respectively. For this expansion.
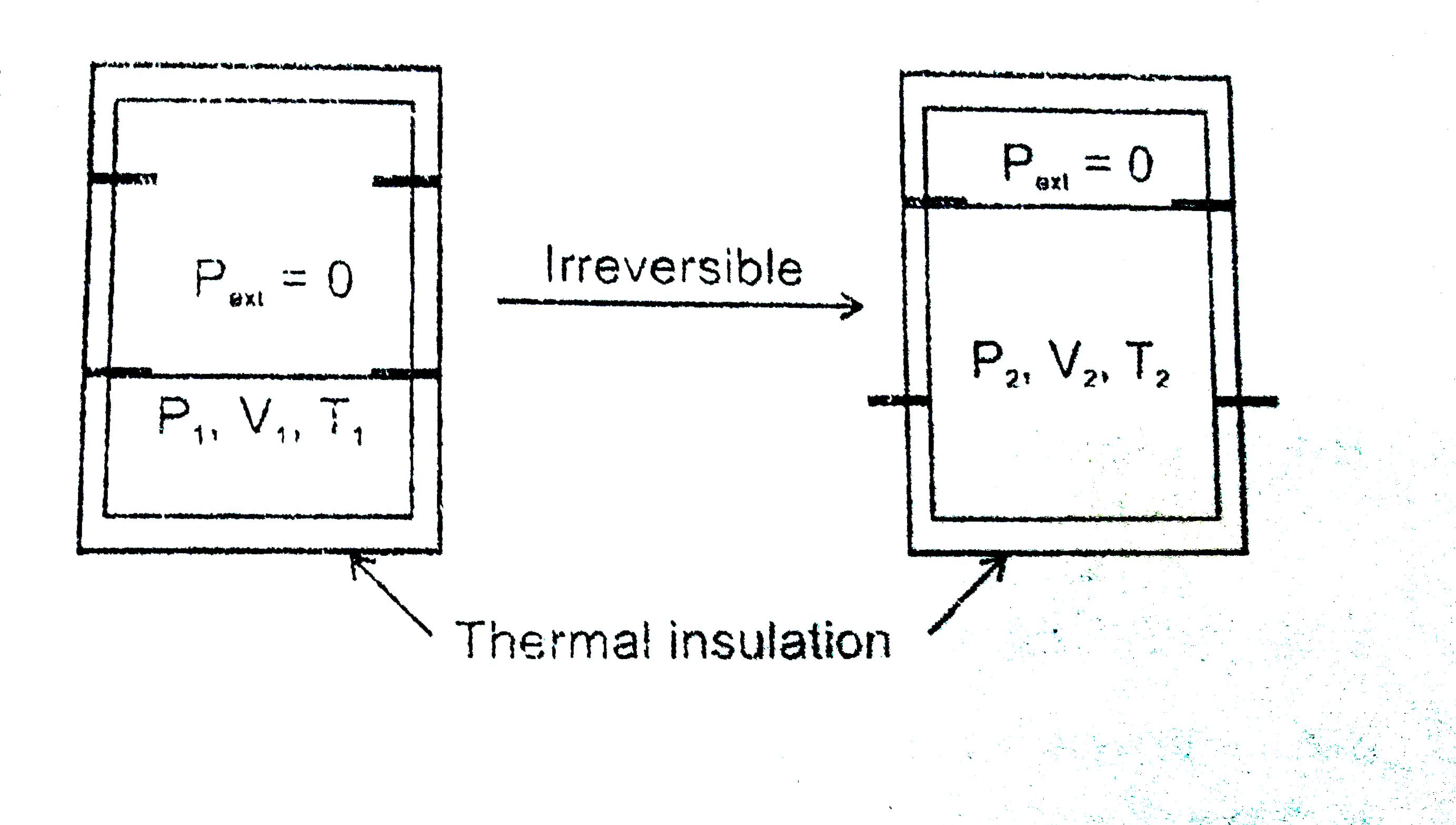 Aq=0BT2=T1CP2V2=PtV1DP2Vγ2=P1Vγ1
Aq=0BT2=T1CP2V2=PtV1DP2Vγ2=P1Vγ1An ideal gas in thermally insulated vessel at internal (pressure)=P1,(volume)=V1 and absolute temperature=T1 expands irreversiby against zero external, pressure , as shown in the diagram,
The final internal pressure, volume and absolute temperature of the gas are p2,V2andT2, respectively . For this expansion
 Aq=0BT2=T1Cp2V2=p1V1DP2Vγ2=P1Vγ2
Aq=0BT2=T1Cp2V2=p1V1DP2Vγ2=P1Vγ2Two containers of equal volume contain the same gas at pressure P1 and P2 and absolute temperature T1 and T2, respectively. On joining the vessels, the gas reaches a common pressure P and common temperature T. The ratio P/T is equal to
Ap1T2+p2T1T1×T2Bp1T2+p2T1T1+T2C12[p1T2+p2T1T1T2]Dp1T2−p2T1T1×T2]
An ideal gas in a thermally insulated vessel at internal pressure =P1, volume =V1 and absolute temperature =T1 expands irreversibly against zero external pressure, as shown in the diagram. The final internal pressure, volume and absolute temperature of the gas are P2,V2 and T2 respectively. For this expansion.
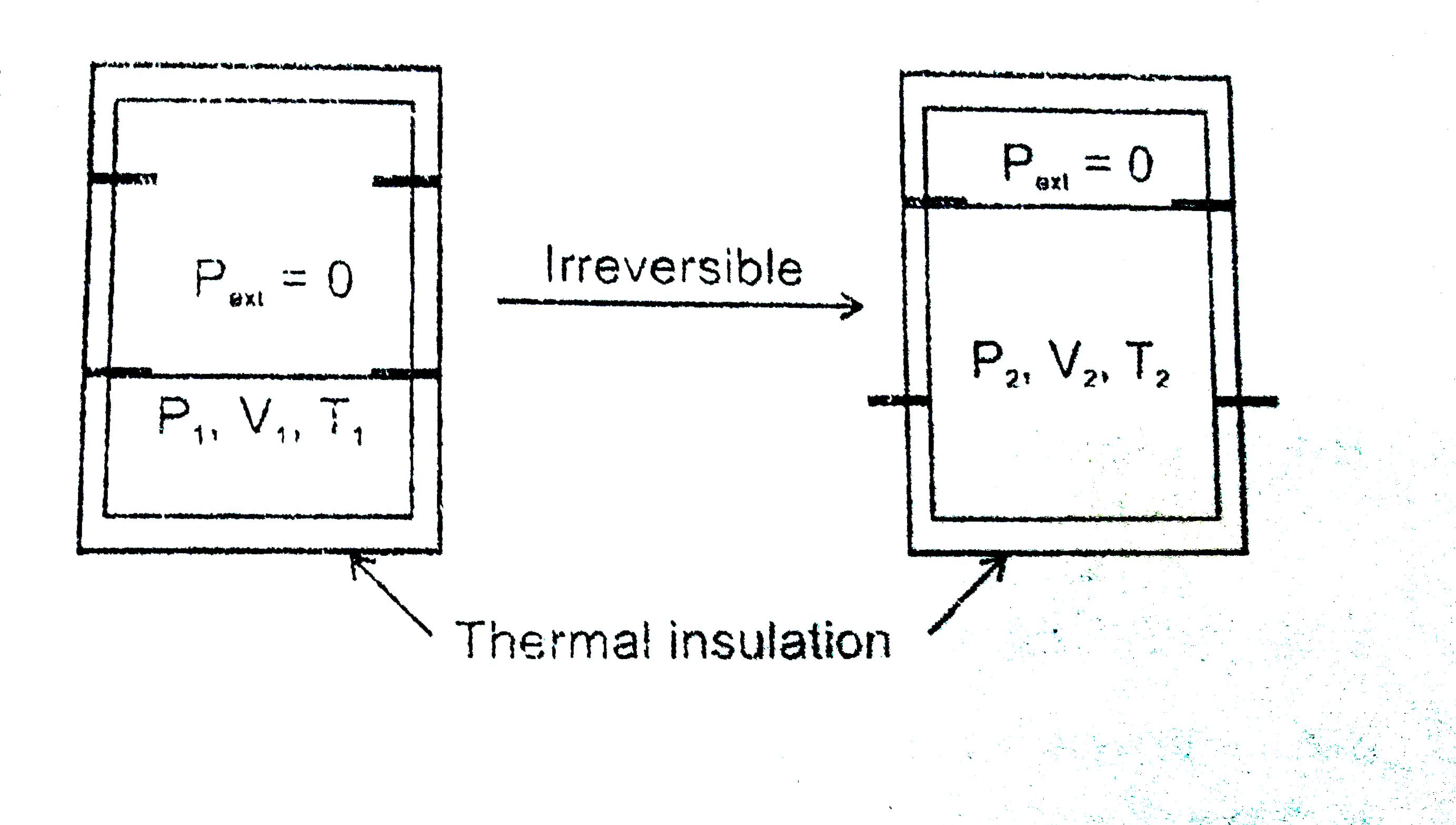
View SolutionTwo containers of equal volume contain the same gas at pressure P1 and P2 and absolute temperature T1 and T2, respectively. On joining the vessels, the gas reaches a common pressure P and common temperature T. The ratio P/T is equal to
View SolutionTwo containers of equal volume contain the same gas at pressure P1 and P2 and absolute temperature T1 and T2, respectively. On joining the vessels, the gas reaches a common pressure P and common temperature T. The ratio P/T is equal to
View SolutionTwo containers of equal volume contain the same gas at pressure P1 and P2 and absolute temperature T1 and T2, respectively. On joining the vessels, the gas reaches a common pressure P and common temperature T. The ratio P/T is equal to
View SolutionIf P, V and T stand for pressure, volume and absolute temperature of a gas, which of the following will be true for Boyle's Law
View Solution
