An object moves along x-axis such that its position varies with time according to the relation $x = 50 t - 5 t^{2}$
Here, x is in meters and time is in seconds. Find the displacement and distance travelled for the time interval t = 0 to t = 6 s.

Video Solution

Text Solution

Verified by Experts

Displacement = change in position
$\Rightarrow Displacement = x_{6} - x_{0} = [50 \times 6 - 5 {(6)}^{2}] - [50 \times 0 - 5 {(0)}^{2}]$
$= (300 - 180) - 0$
$= 120 m$
Distance travelled for an object moving along a straight line can be equal to displacement when the particle does not turn back. To find, whether there is a turning point or not, find the point where velocity becomes zero
As $v = \frac{d x}{d t} \Rightarrow v = 50 - 10 t .$
Put $v = 0, 0 = 50 - 10 t \Rightarrow t = 5 s .$
This value t = 5 s lies between the interval 0 - 6 s.
So, we have to describe the exact path.
The position at t = 0 is $x_{0} = 50 \times 0 - 5 {(0)}^{2} = 0$
The position at t = 5 s is $x_{5} = 50 \times 5 - 5 {(5)}^{2} = 125 m$
The position at t = 6 s is $x_{6} = 50 \times 6 - 5 {(6)}^{2} = 120 m .$
So, the object moves as shown.

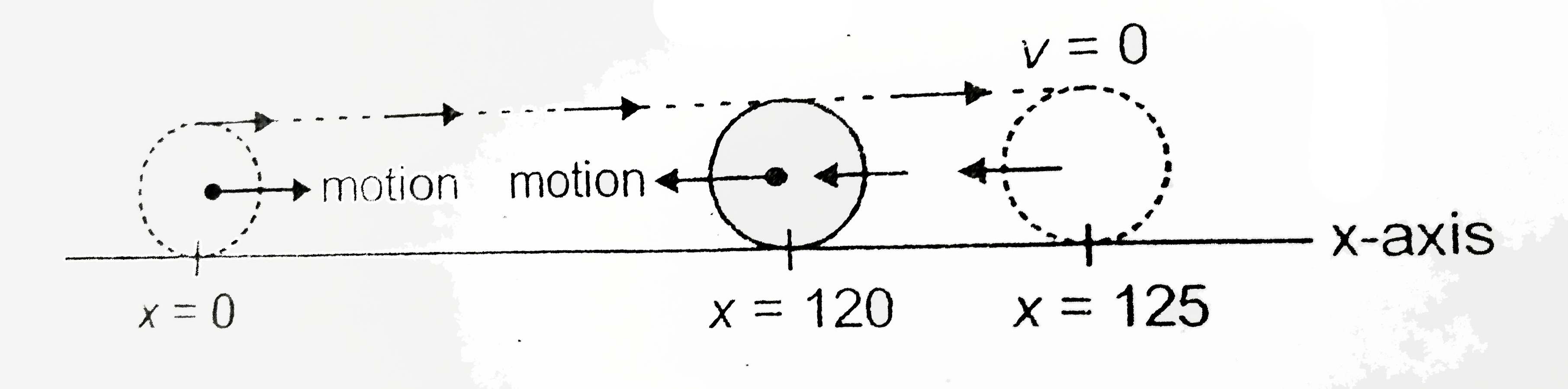
$Distance travelled = 125 m (in forward direction) + 5 m (in backward direction)$
$= 130 m .$

Updated on:21/07/2023

A particle moves along the x-axis such that its co-ordinate (x) varies with time (t), according to the expression $x = 2 - 5 t + 6 t^{2},$ where x is in metres and t is in seconds. The initial velocity of the particle is :–
A $- 5 m / s$
B $- 3 m / s$
C $6 m / s$
D $2 m / s$
A particle moves along x-axis such that its position veries with time as $x = 50 t - 5 t^{2}$ . Select the correct alternative (s).
AThe particle has travelled 130m distance by $t = 6 s$ .
BAt $t = 4 s$ and $t = 12 s$ , the particle is at 120 m distance from starting point.
Cthe particle will never be at a distance of 130 m from starting point.
DDuring the whole motion, the particle does not have same velocity at 2 different instants.
A particle moves along X-axis in such a way that its coordinate X varies with time t according to the equation $x = (2 - 5 t + 6 t^{2}) m$ . The initial velocity of the particle is
A $- 5 m / s$
B $6 m / s$
C $- 3 m / s$
D $3 m / s$