The position of a particle varies with time according to the relation x=3t2+5t3+7t, where x is in m and t is in s. Find
(i) Displacement during time interval t = 1 s to t = 3 s.
(ii) Average velocity during time interval 0 - 5 s.
(iii) Instantaneous velocity at t = 0 and t = 5 s.
(iv) Average acceleration during time interval 0 - 5 s.
(v) Acceleration at t = 0 and t = 5 s.
x=3t2+5t3+7t
(i) x1=3(1)2+5(1)3+7×1=15 Δx=x3−x1=168m
x3=3(3)2+5(3)3+7×3=183
(ii) vav=ΔxΔt=x5−x05−0=3(5)2+5(5)3+7×55−0=147m/s
(iii) V=dxdt=6t+15t2+7 V0=7m/s V5=412m/s
(iv) aav=ΔVΔt=V5−V05−0=412−75=81m/s Note : aav≠Avg. velocitytime
(v) a=dvdt=6+30t
(v) a=dvdt=6+30t
a0=6m/s2,a5=156m/s2
Topper's Solved these Questions
- MOTION IN STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN STRAIGHT LINEExercise:Try Yourself
Explore 40 Videos
- MOTION IN STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN STRAIGHT LINEExercise:Assignment (SECTION - A)
Explore 50 Videos
- MOTION IN A STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN A STRAIGHT LINEExercise:ASSIGNMENT (SECTION - D)
Explore 15 Videos
- MOVING CHARGE AND MAGNESIUMBook:AAKASH INSTITUTEChapter:MOVING CHARGE AND MAGNESIUMExercise:SECTION D
Explore 16 Videos
Similar Questions
The position of an object moving on a straight line is defined by the relation x=t3−2t2−4t, where x is expressed in meter and t in second. Determine
(a) the average velocity during the interval of 1 second to 4 second.
(b) the velocity at t = 1 s and t = 4 s,
(c) the average acceleration during the interval of 1 second to 4 second.
(d) the acceleration at t = 4 s and
View SolutionThe displacement of a particla moving in straight line is given by s=t4+2t3+3t2+4, where s is in meters and t is in seconds. Find the
(a) velocity at t=1s, (b) acceleration at t=2s,
(c ) average velocity during time interval t=0 to t=2s and
(d) average acceleration during time interval t=0 to t=1s.
View Solution
Knowledge Check
The position of a particle moving on the x-axis is given by x=t3+4t2−2t+5 where x is in meter and t is in seconds
(i) the velocity of the particle at t=4s is 78m/s
(ii) the acceleration of the particle at t=4s is 32m/s2
(iii) the average velocity during the interval t=0 to t=4sis 30m/s
(iv) the average acceleration during the interval t=0 to t=4s is 20m/s2A(i), (ii)B(ii), (iii)C(i), (ii), (iii)DAllThe displacement of a body of mass 2 kg varies with time t as S=t2+2t, where S is in m and t is in s. The work done by all the forces acting on the body during the time interval t=2 to t=4 s is
A36 JB64 JC100 JD120 JPosition of a particle at any instant is given by x=3t2+1 , where x is in m and t in sec. Its average velocity in the time interval t=2 sec to t=3 sec will be :
A15m/sB12m/sC18m/sD6m/s
Find average speed in time interval t= 2 to t=10s
View SolutionThe position of a particle moving along the straight line is given as s= (t^(2)-4t+3)m where t is time in s .The magnitude of displacement of the particle during time interval t=0 to till its velocity becomes zero
View SolutionAn object moves along x-axis such that its position varies with time according to the relation x=50t−5t2
Here, x is in meters and time is in seconds. Find the displacement and distance travelled for the time interval t = 0 to t = 6 s.
View SolutionThe v-t graph for a particle moving along x-axis is shown in the figure, find
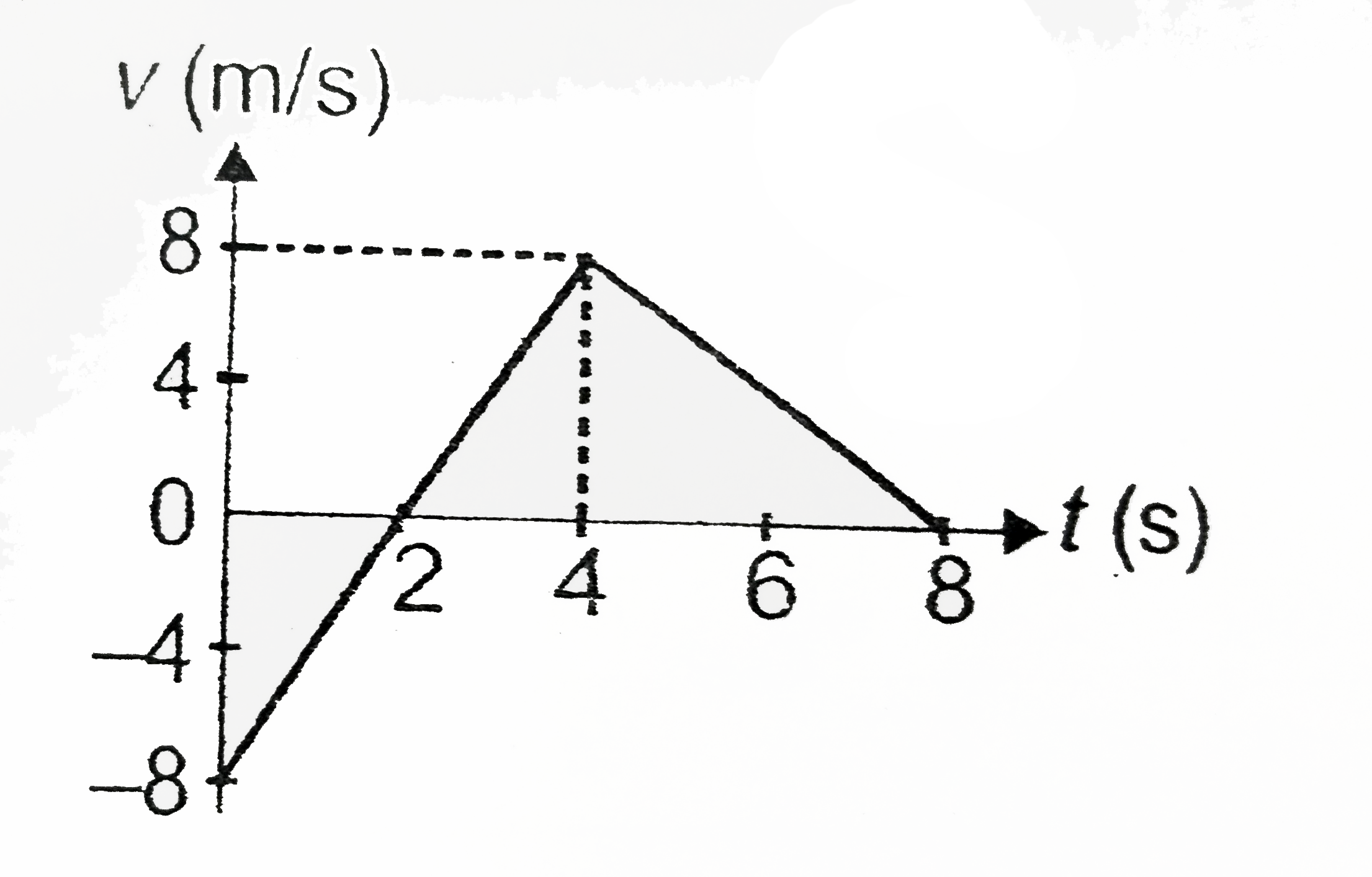
(a) Average velocity in the interval 0 to 8 s.
(b) Average speed in the interval 0 to 8 s.
(c) Average acceleration in the interval 0 to 4 s.
(d) Instantaneous acceleration at t = 2.5 s.
View SolutionThe displacement x of a particle is dependent on time t according to the relation : x=3−5t+2t2. If t is measured in seconds and s in metres, find its acceleration at t = 4s.
View Solution