A particle starts from the origin, goes along x-axis to the point (10 m, 0) and then returns along. The same line to the point (-10 m, 0). The distance and displacement of the particle during the trip are
20 m, 0
30 m, 10 m
30 m, - 10 m
20 m, 10 m
The correct Answer is:C
To solve the problem, we will calculate both the distance and displacement of the particle during its trip.
1. Understanding the Motion:
- The particle starts at the origin (0 m).
- It moves to the point (10 m, 0) along the x-axis.
- Then, it returns along the same line to the point (-10 m, 0).
2. Calculating the Distance:
- The distance is the total length of the path traveled by the particle.
- First, the particle travels from 0 m to 10 m, which is a distance of 10 m.
- Then, it returns from 10 m to -10 m. The distance for this return journey is:
- From 10 m to 0 m: 10 m
- From 0 m to -10 m: 10 m
- Therefore, the total distance traveled is:
Total Distance=10m+10m+10m=30m
3. Calculating the Displacement:
- Displacement is defined as the change in position from the initial point to the final point.
- The initial position is 0 m and the final position is -10 m.
- Therefore, the displacement is:
Displacement=Final Position−Initial Position=−10m−0m=−10m
Final Answers:
- Distance: 30 m
- Displacement: -10 m
- The particle starts at the origin (0 m).
- It moves to the point (10 m, 0) along the x-axis.
- Then, it returns along the same line to the point (-10 m, 0).
- The distance is the total length of the path traveled by the particle.
- First, the particle travels from 0 m to 10 m, which is a distance of 10 m.
- Then, it returns from 10 m to -10 m. The distance for this return journey is:
- From 10 m to 0 m: 10 m
- From 0 m to -10 m: 10 m
- Therefore, the total distance traveled is:
Total Distance=10m+10m+10m=30m
- Displacement is defined as the change in position from the initial point to the final point.
- The initial position is 0 m and the final position is -10 m.
- Therefore, the displacement is:
Displacement=Final Position−Initial Position=−10m−0m=−10m
- Distance: 30 m
- Displacement: -10 m
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - B)19videos
MOTION IN STRAIGHT LINE
- BOOK - AAKASH INSTITUTECHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - C)7videos
MOTION IN STRAIGHT LINE
- BOOK - AAKASH INSTITUTECHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Try Yourself40videos
MOTION IN STRAIGHT LINE
- BOOK - AAKASH INSTITUTECHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - D)15videos
MOTION IN A STRAIGHT LINE
- BOOK - AAKASH INSTITUTECHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION D16videos
MOVING CHARGE AND MAGNESIUM
Similar Questions
A particle starts from the origin, goes along the X-axis to the pont (20m, 0) and then returns along the same line to the point (-20m,0). Find the distance and displacement of the particle during the trip.
View SolutionA particle starts from the origin,goes along the "X" - axis to the point(20m,0) and then returns along the same line to the point (-20m,0 then the displacement of the particle during the trip in negative direction is....(in m )
View Solution
Knowledge Check
- Question 1 - Select One
A particle starts from the origin, goes along X-axis to the point (30m, 0) and then returns along the same line to the point (-30m,0). The displacement and distance of the particle during the trip are
A0, 60mB60m,30mC90m, -30mD−30m,90m - Question 2 - Select One
A force F=−K(yˆi+xˆj) (where K is a positive constant) acts on a particle moving in the x-y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0), and then parallel to the y-axis to the point (a,a). The total work done by the force F on the particle is
A−2Ka2B2Ka2C−Ka2DKa2 - Question 3 - Select One
A force F=−K(yˆi+xˆj) (where K is a positive constant) acts on a particle moving in the x-y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0), and then parallel to the y-axis to the point (a,a). The total work done by the force F on the particle is
A−2Ka2B2Ka2C−Ka2DKa2
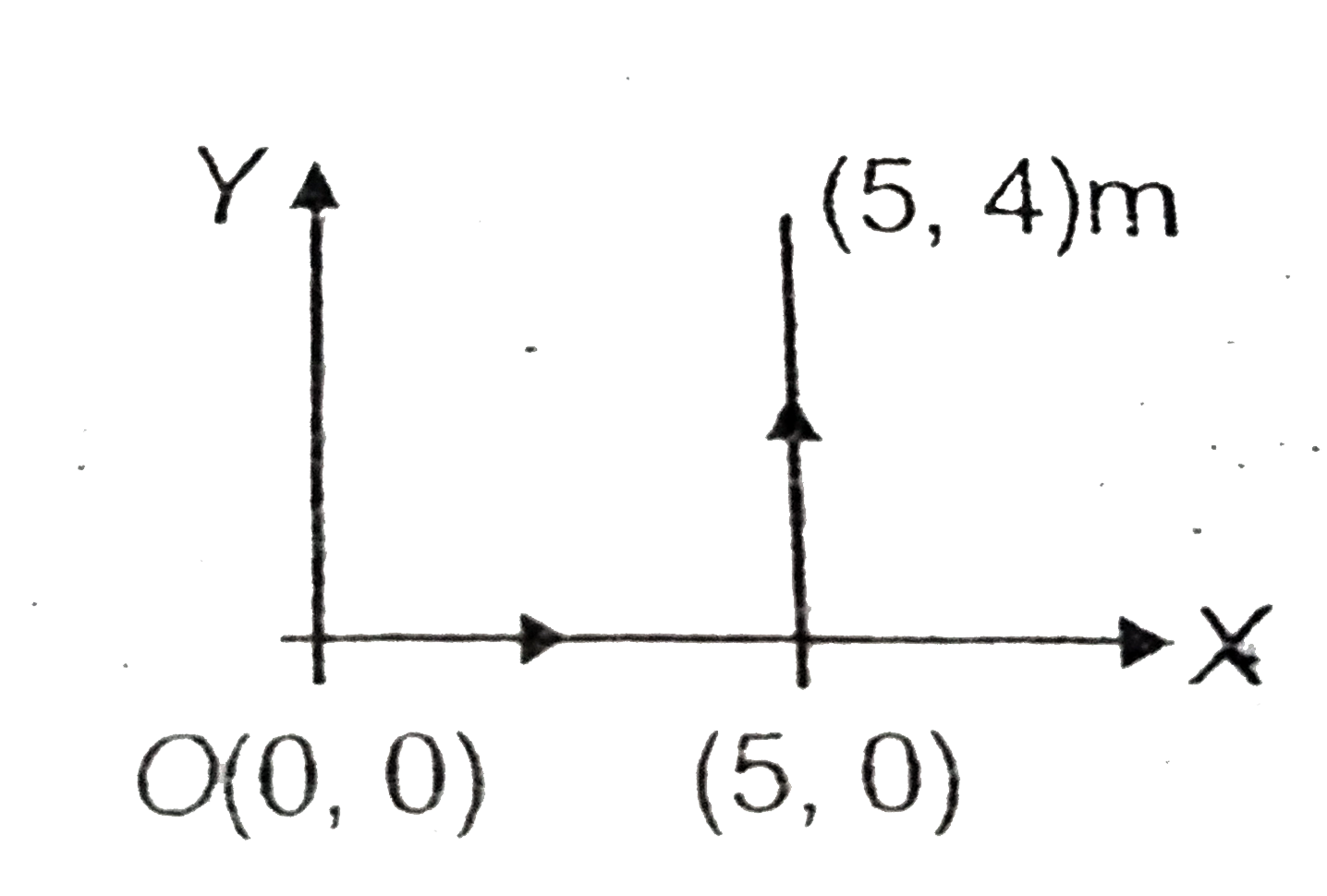
A force →F=(4ˆi+5ˆj)N acts on a particle moving in XY plane. Starting from origin, the particle first goes along x-axis to the point (5.0) m and then parallel to the Y-axis to the point (5,4 m. The total work done by the force on the particle is
 View Solution
View SolutionA particle starts from the origin and moves along a stright line If the velocity of the particle at time t seconds 10t cm/s then find the distance traversed during fist seconds after the start.
View SolutionA force →F(yˆl+xˆJ), where K is a positive constant, acts on a particle moving in the XY-Plane. Starting from the origin, the particle is taken along the positive X-axis to a point (a,0) and then parallel to the y-axis to the point (a,a). Calculate the total work done by the force on the particle.
View SolutionA force →F=(3→i+4→j)N, acts on a particle moving in x-y plane. Starting from origin, the particle first goes along x-axis to thepoint (4,0)m and then parallel to the y -axis to the point(4, 3)m. The total work done by the force on the particle is
(##NAR_NEET_PHY_XI_P2_C06_E09_014_Q01.png" width="80%">View SolutionA force F=−K(yˆI+xˆj)(whereKisaposiveconstant)actsonapartic≤mov∈g∈thexypla≠.Start∈gformtheorig∈al,theparticalistakenalong∈thepositivexaξs→thep∮(x,0)andthenpartical→theyaξsthep∮(x,0).The→talworkdo≠bytheforceF on the particls is
View Solution

