Consider objects of masses $m_{1} and m_{2}$ moving initially along the same straight line with velocities $u_{1} and u_{2}$ respectively. Considering a perfectly elastic collision (with $u_{1} > u_{2})$ derive expressions for their velocities after collision.

Video Solution

Text Solution

Verified by Experts

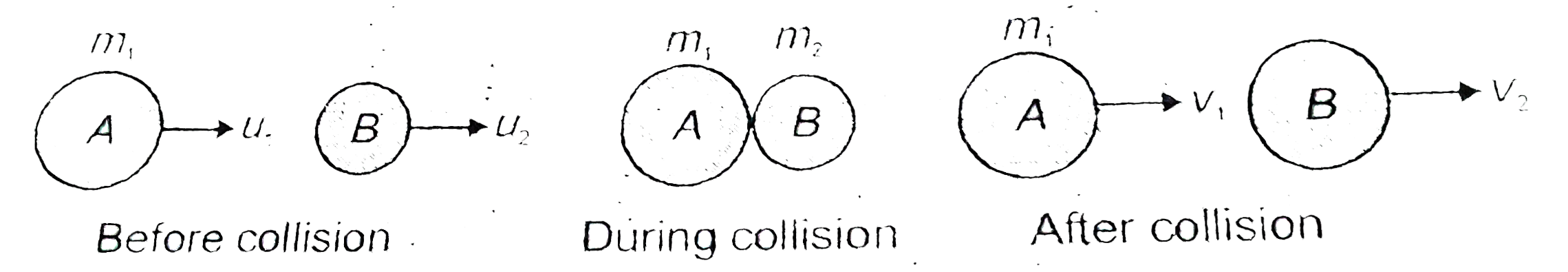
With $u_{1} > u_{2}$
Relative velocity of approach before collision $= u_{1} - u_{2} \dots (i)$
Let the veocity of A after collision be $v_{1}$ and the velocity of B after collision be $v_{2} .$
When $v_{2} > v_{1},$ teh bodies separate after collision.
Relative velocity of spearafion after collision $= v_{2} - v_{1} ... (i)$
Linear momentum of the two balls before colision $= v_{2} - v_{1} ... (i i)$
Linear momentum of the two balls before collision $= m_{1} r_{1} + m_{2} u_{2}$
Linear momentum of hte two balls after colision $= m_{1} v_{1} + m_{2} v_{2}$
$m_{1} v_{1} + m_{2} v_{2} = m_{1} u_{1} + m_{2} u_{2} ... (i i i)$
According to the law of conservation of linear momentum
or $m_{2} (v_{2} - u_{2}) = m_{1} (u_{1} - v_{1}) ... (i v)$
Total KE of the two balls before collision $= \frac{1}{2} m_{1} u_{1}^{2} + \frac{1}{2} m_{2} u_{2}^{2} ... (v)$
Total KE of the two balls after collision
$= \frac{1}{2} m_{1} v_{1}^{2} + \frac{1}{2} m_{2} v_{2}^{2} ... (v i)$
$\frac{1}{2} m_{1} v_{1}^{2} + \frac{1}{2} m_{2} v_{2}^{2} = \frac{1}{2} + \frac{1}{2} m_{2} u_{2}^{2}$ According to the law of conservation of KE $\frac{1}{2} m_{2} (v_{2}^{2} - u_{2}^{2}) = \frac{1}{2} (u_{1}^{2} - y_{1}^{2})$
or $m_{2} (v_{2}^{2} - u_{2}^{2}) = m_{1} (u_{1}^{2} - v_{1}^{2}) ... (v i i)$
Dividing equation (vii) by equation (iv),
$\frac{m_{2} (v_{2}^{2} - u_{2}^{2})}{m_{2} (v_{2} - u_{2})} = \frac{m_{1} (u_{1}^{2} - v_{1}^{2})}{m_{1} (u_{1} - v_{1})}$
$\frac{(v_{2} + u_{2}) (v_{2} - u_{2})}{(v_{2} - u_{2})} = \frac{(u_{1} + v_{1}) (u_{1} - v_{1})}{(u_{1} - v_{1})}$
or $v_{2} + u_{2} = u_{1} + v_{1}$
or $v_{2} - v_{1} = u_{1} - u_{2} ... (v i i i)$
Hence in one-dimensional elastic collision (from equationa (i) & (ii))
From equation (viii) , $\frac{v_{2} - v_{1}}{u_{1} - u_{2}} = 1$
By definition, $\frac{v_{2} - v_{1}}{u_{1} - u_{2}} = 0 = 1$
Hence, coefficient fo restitution/resilience of a perfectly elastic collision in one dimension is unity From equation (viii), $... (i x)$
$v_{2} = u_{1} - u_{2} + v_{1}$
Put this value in equation (iii)
$m_{1} v_{1} + m_{2} (u_{1} - u_{2} + v_{1}) = m_{1} u_{1} + m_{2} u_{2}$
$m_{1} v_{1} + m_{2} u_{1} - m_{2} u_{2} + m_{2} v_{1} = m_{1} u_{1} + m_{2} u_{2}$
$v_{1} (m_{1} + m_{2}) = (m_{1} - m_{2}) u_{1} + 2 m_{2} u_{2}$
$v_{1} = \frac{(m_{1} - m_{2}) u_{1}}{(m_{1} + m_{2})} + \frac{2 m_{2} u_{2}}{m_{1} + m_{2}} ... (x)$
Put this value of $v_{1}$ fro equation (x) in equation (ix)
$v_{2} = u_{1} - u_{2} + \frac{(m_{1} - m_{2}) u_{1}}{m_{1} + m_{2}} + \frac{2 m_{2} u_{2}}{m_{1} + m_{2}}$
$= u_{1} [1 + \frac{m_{1} - m_{2}}{m_{1} + m_{12}}] + u_{2} [\frac{2 m_{2}}{m_{1} + m_{2}} - 1]$
$= u_{1} [\frac{m_{1} + m_{2} + m_{1} - m_{2}}{m_{1} + m_{2}}] + u_{2} [\frac{2 m_{2} - m_{1} - m_{2}}{m_{1} + m_{2}}]$
$v_{2} = \frac{2 m_{1} u_{1}}{m_{1} + m_{2}} + \frac{(m_{2} - m_{1}) u_{2}}{(m_{1} + m_{2})} ... (x i)$
Note: You can get exp. for $v_{2}$ from equation (x) by interchanging $m_{1} and m_{2} and u_{1} and u_{2}$ You can also get equation (x) from equation (xi).

Updated on:21/07/2023

Two equal masses $m_{1}$ and $m_{2}$ moving along the same straight line with velocites $+ 3 m / s$ and $- 5 m / s$ respectively collide elastically. Their velocities after the collision will be respectively.
A $+ 4 m / s$ for both
B $- 3 m / s and + 5 m / s$
C $- 4 m / s and + 4 m / s$
D $- 5 m / s and + 3 m / s$
Two particles of same mass m moving with velocities $u_{1}$ and $u_{2}$ collide perfectly inelastically. The loss of energy would be :
A $1 / 2 m {(u_{1} - u_{2})}_{1}^{2}$
B $1 / 4 m {(u_{1} - u_{2})}_{1}^{2}$
C $m {(u_{1} - u_{2})}_{1}^{2}$
D $2 m {(u_{1} - u_{2})}_{1}^{2}$
Two identical mass M moving with velocity $u_{1} and u_{2}$ collide perfectly inelastically. The loss in kinetic energy is
A $\frac{M}{2} {(u_{2} - u_{1})}_{2}^{2}$
B $\frac{M}{2} (u_{1}^{2} - u_{2}^{2})$
C $\frac{M}{4} {(u_{2} - u_{1})}_{2}^{2}$
D $\frac{M}{4} (u_{1}^{2} - u_{2}^{2})$