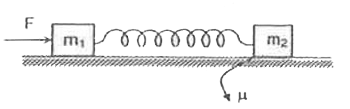
For Q. 25 find the minimum constant force to be applied to body of mass $m_{1}$ in order to shift body of mass $m_{2} .$ Take $m_{1} = m_{2} = 10 k g, μ = 0.5$

Text Solution

Verified by Experts

$F . x = μ m_{1} g x - \frac{1}{2} k x^{2} = 0 ... (i)$
But $K x = μ_{2} g .$ (for just moving body of mass $m_{2})$
Put the value of K in (i) to get F.
F.x $- μ m_{1} g x - \frac{1}{2} k x^{2} = 0$
But $k x = μ m_{2} g$ (for moving body of mass $m_{2}$ )
$F x - μ m_{1} g x - \frac{1}{2} (\frac{μ m_{2} g}{x}) x^{2} = 0$
$F = μ m_{1} g + \frac{1}{2} μ m_{2} g$
$= μ (m_{1} + \frac{m_{2}}{2}) g$
$= 0.5 (10 + \frac{10}{2}) 10$
$= 75 N$

Updated on:21/07/2023

Two block of masses $m_{1}$ and $m_{2}$ connected by a light spring rest on a horizontal plane. The coefficient of friction between the block and the surface is equal to $μ$ . What minimum constant force has to be applied in the horizontal direction to the block of mass $m_{1}$ in order to shift the other block?
A8 N
B15 N
C10 N
D25 N
Two blocks of masses $m_{1}$ and $m_{2}$ are connected by a spring having spring constant K. Initially , the spring is at its natural length. The coefficient of friction between the blocks and the surface is $μ$ . What minimum constant force has to be applied in the horizontal direction to the block of mass $m_{1}$ , in order to shift the other block ?
A $F = μ (m_{1} + \frac{m_{2}}{2}) g$
B $F = μ (\frac{m_{1}}{2} + m_{2}) g$
C $F = μ (m_{1}^{2} + \frac{m_{2}^{2}}{2}) g$
D $F = μ^{2} (m_{1}^{2} + \frac{m_{2}}{2}) g$