A block A has a mass m1=2kg and is attached to a spring of spring consstant 50 N/m. Another block of mass 4 kg is pressed against A, so that the spring is compressed by a distance d. Then find the maximum value of d (in metre) for which on release of B. the block A does no lose contact from wall. (Friction coefficient μ=0.5).
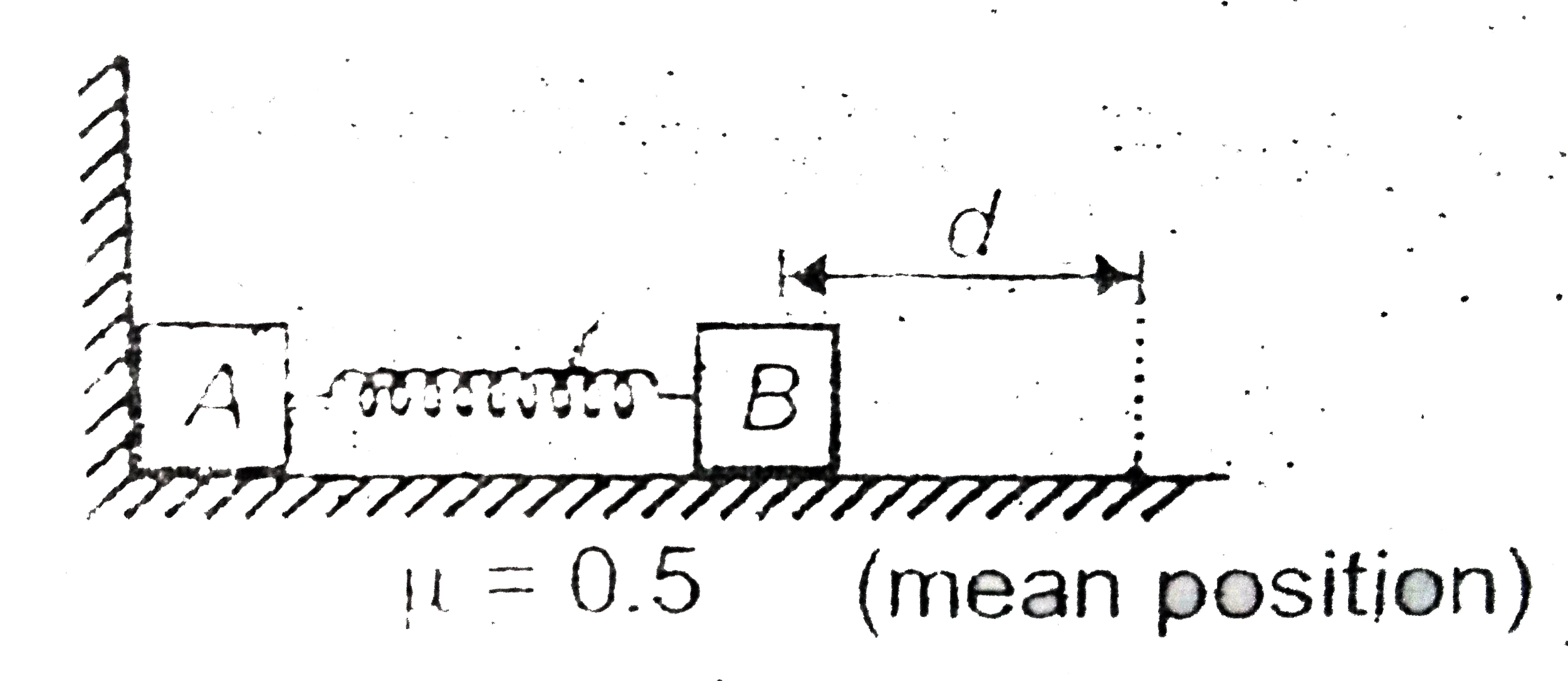
The correct Answer is:1
Step by step video & image solution for A block A has a mass m_(1)=2 kg and is attached to a spring of spring consstant 50 N/m. Another block of mass 4 kg is pressed against A, so that the spring is compressed by a distance d. Then find the maximum value of d (in metre) for which on release of B. the block A does no lose contact from wall. (Friction coefficient mu=0.5). by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTECHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-H (MULTIPLE TRUE FALSE TYPE QUESTIONS)
10 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTECHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-I (SUBJECTIVE TYPE QUESTIONS)
6 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTECHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-F (MATRIX-MATCH TYPE QUESTIONS)
4 Videos
- WAVESBOOK - AAKASH INSTITUTECHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
The block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionA block of mass 0.1 kg attached to a spring of spring constant 400 N/m is pulled rightward from x0=0 to x1=15 mm. Find the work done by spring force.
View Solution
Knowledge Check
a block of mass 0.1 kg attached to a spring of spring constant400Nm pulled horizontally from x=0 tox1=10mm. Find the work done by the spring force
A2⋅10−2JB2⋅10−6JC3⋅10−6JD4⋅10−2JTwo blocks of masses 6 kg and 3 kg are attached to the two ends of a massless spring of spring constant 2π2N/m. If spring is compressed and released on a smooth horizontal surface then find the time period (in seconds) of each block.
A1B2C3D4A block of mass m rigidly attached with a spring k is compressed through a distance A. If the block is released, the period of oscillation of the block for a complete cycle is equal to
 A4π3√mkBπ√2√mkC2π3√mkDNone of these
A4π3√mkBπ√2√mkC2π3√mkDNone of these
A block of mass m moving at a speed v0 compresses a spring of spring constant k as shown in the figure. Find (a) the maximum compression of spring and (b) speed of the block when the spring is compressed to half of maximum compression.
View SolutionA block of mass M = 4 kg is kept on a smooth horizontal plane. A bar of mass m = 1 kg is kept on it. They are connected to a spring as shown & the spring is compressed. Then what is the maximum compression in the spring for which the bar will not slip on the block when released if coefficient of friction between them is 0.2 & spring constant = 1000 N/m : (Take g=10m/s2)

View SolutionIn the figure shown, all surfaces are smooth and force constant of spring is 10N/m. Block of mass (2 kg) is attaced with the spring. The spring is compressed by (2m) and then released. Find the maximum distance d travelled by the block over the inclined plane. Take g=10m/s2.
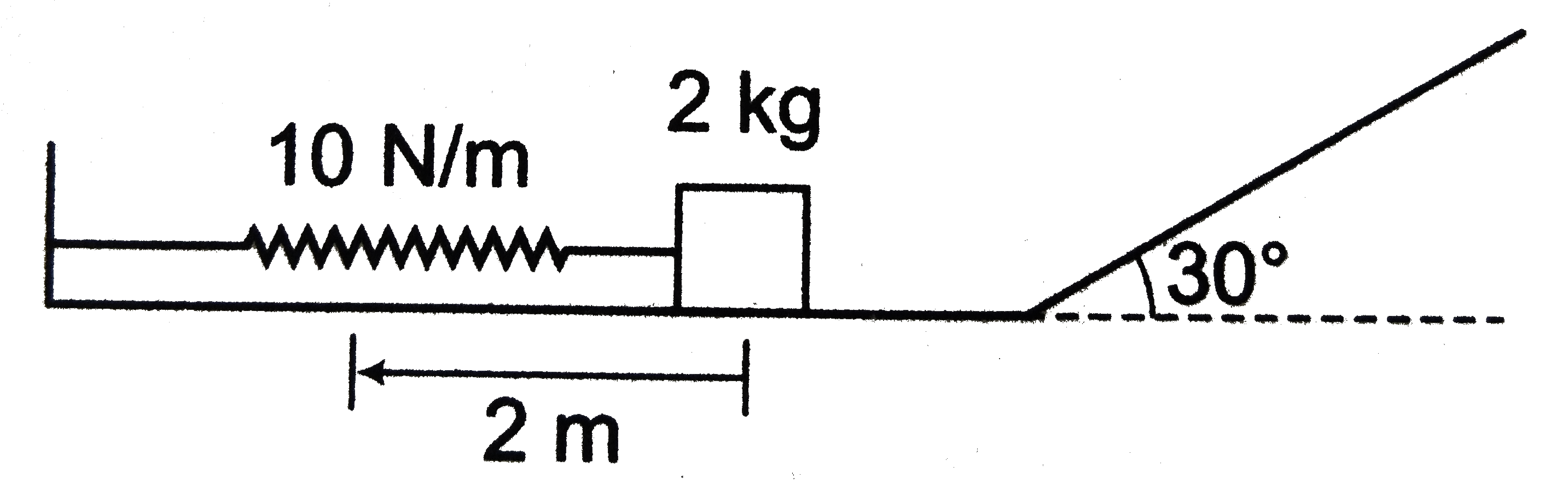 .
.
View SolutionA spring of force constant k = 100 N/m is compressed to x = 0.05 m by a block of mass 1 kg and released.Find the distance d where it falls

View SolutionA block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
View Solution
