A particle is acted upon by a force →F=yˆi+xˆj newton. When the particle is moved from (1 m, 1 m) to (9m, 3 m) via straight path, work done by →F is y. What is the value of xy?
The correct Answer is:1
To solve the problem, we need to calculate the work done by the force →F=y^i+x^j when a particle moves from point A (1 m, 1 m) to point B (9 m, 3 m) along a straight path. The work done is given as y.
1. Identify the Force and Path:
The force acting on the particle is given by:
→F=y^i+x^j
The initial position (point A) is (x1,y1)=(1,1) and the final position (point B) is (x2,y2)=(9,3).
2. Displacement Vector:
The displacement vector d→r can be expressed as:
d→r=dx^i+dy^j
3. Work Done Calculation:
The work done W by the force when moving from point A to point B is given by the line integral:
W=∫BA→F⋅d→r
Substituting the expressions for →F and d→r:
W=∫BA(y^i+x^j)⋅(dx^i+dy^j)=∫BA(ydx+xdy)
4. Setting Up the Limits:
We need to integrate with respect to x and y. The limits for x are from 1 to 9, and for y from 1 to 3.
5. Calculate the Work Done:
We can break the integral into two parts:
W=∫91ydx+∫31xdy
- For the first integral, since y is changing from 1 to 3, we can express y in terms of x using the straight line equation connecting points A and B. The slope of the line is:
slope=3−19−1=28=14
Thus, the equation of the line is:
y−1=14(x−1)⟹y=14x+34
- Now substituting y into the first integral:
W1=∫91(14x+34)dx
- For the second integral, we can substitute x in terms of y using the same line equation:
x=4y−1
Thus:
W2=∫31(4y−1)dy
6. Evaluating the Integrals:
- For W1:
W1=(18x2+34x)91=(18(81)+274)−(18(1)+34)
- For W2:
W2=(2y2−y)31=(2(9)−3)−(2(1)−1)
7. Final Calculation:
After calculating both integrals, we combine them to find the total work done W and set it equal to y. From this, we can solve for the ratio xy.
8. Finding the Ratio:
After simplifying the equations, we find:
7y+2x=0⟹xy=−72
Final Answer:
The value of xy is −72.
The force acting on the particle is given by:
→F=y^i+x^j
The initial position (point A) is (x1,y1)=(1,1) and the final position (point B) is (x2,y2)=(9,3).
The displacement vector d→r can be expressed as:
d→r=dx^i+dy^j
The work done W by the force when moving from point A to point B is given by the line integral:
W=∫BA→F⋅d→r
Substituting the expressions for →F and d→r:
W=∫BA(y^i+x^j)⋅(dx^i+dy^j)=∫BA(ydx+xdy)
We need to integrate with respect to x and y. The limits for x are from 1 to 9, and for y from 1 to 3.
We can break the integral into two parts:
W=∫91ydx+∫31xdy
- For the first integral, since y is changing from 1 to 3, we can express y in terms of x using the straight line equation connecting points A and B. The slope of the line is:
slope=3−19−1=28=14
Thus, the equation of the line is:
y−1=14(x−1)⟹y=14x+34
W1=∫91(14x+34)dx
- For the second integral, we can substitute x in terms of y using the same line equation:
x=4y−1
Thus:
W2=∫31(4y−1)dy
- For W1:
W1=(18x2+34x)91=(18(81)+274)−(18(1)+34)
- For W2:
W2=(2y2−y)31=(2(9)−3)−(2(1)−1)
After calculating both integrals, we combine them to find the total work done W and set it equal to y. From this, we can solve for the ratio xy.
After simplifying the equations, we find:
7y+2x=0⟹xy=−72
The value of xy is −72.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-H (MULTIPLE TRUE FALSE TYPE QUESTIONS)10videos
WORK, ENERGY AND POWER
- BOOK - AAKASH INSTITUTECHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-I (SUBJECTIVE TYPE QUESTIONS)6videos
WORK, ENERGY AND POWER
- BOOK - AAKASH INSTITUTECHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-F (MATRIX-MATCH TYPE QUESTIONS)4videos
WORK, ENERGY AND POWER
- BOOK - AAKASH INSTITUTECHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))12videos
WAVES
Similar Questions
Knowledge Check
- Question 1 - Select One
A force F=(3xˆi+4ˆj) Newton (where x is in metres) acts on a particle which moves from a position (2m, 3m) to (3m, 0m). Then the work done is
A7.5 JB−12JC−4.5JD+4.5J - Question 2 - Select One
A force acting on particle is given by →F=(3x2ˆi+4yˆj)N. The change in kinetic energy of particle as it moves from (0,2m) to (1m,3m) is
A6JB10JC11JD13J - Question 3 - Select One
A force given by →F=fxˆi+fyˆj+fzˆk acts on a particle which moves from (a, b, c) to (d, e, f). The work done by the force F is : (Here A1,A2,A3 are magntitude of area bounded )
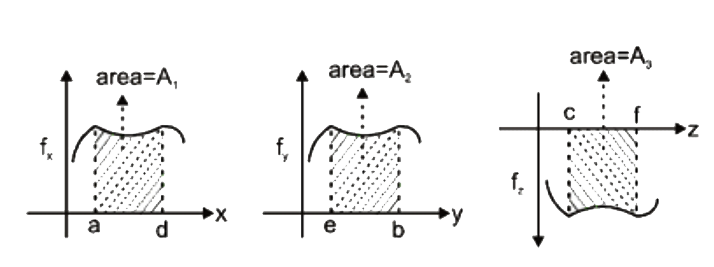 AA1+A2+A3BA1−A2−A3C−A1+A2−A3DA1−A2+A3
AA1+A2+A3BA1−A2−A3C−A1+A2−A3DA1−A2+A3
If force →f=(3x→i+y2) W is acting on a body and body moves from (1m, 2m, 1m) to (2m, 3, 8m), then find the work done due to the force
View SolutionIf particle is acted upon by the forces →F1=2ˆi+2ˆj−3ˆk →F2=5ˆi+cˆj−bˆk
→F3=bˆi+5ˆj−7ˆk,→F4=cˆi+6ˆj−aˆk. Find the values of the constant a, b, c in ordre that the particle will be in equilibrium.View SolutionA particle is acted upon by constant forces →F=−2ˆi+3ˆj+4ˆkand→F2=−ˆi+2ˆj−3ˆk is distanced from the point A (2,1,0,) to the point B(-3,-4,2) Find the work done by forces.
View SolutionCalculate the work done to displace the particle from
(1,2) to (4,5) .if →F=4ˆi+3ˆjView SolutionA particle is acted upon by the forces →F1=2ˆi+aˆj−3ˆk,→F2=5ˆi+cˆj−bˆk,→F3=bˆi+5ˆj−7ˆk,→F4=cˆi+6ˆj−aˆk. Find the values of the constants a, b, c in order that the particle will be in equilibrium.
View Solution

