A smooth ring of mass m1 connected with a hanging block of mass m2, by a long inextensible string, is released from rest. The ring moves vertically along a fixed rigid rod as shown in figure.
Describe the motion of the ring if
(A) m1=2m2
(B) m1=m2
(C ) m1=m22

(A), (B) when m1≥m2,m1 will be never be in equilibrium. It will go on mobing till m2 hits the pulley. (C ) m1 will attain maximum speed at its equilibrium position at θ=60∘ when θ= angle made by string with horizontal.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - WORK, ENERGY AND POWEREXERCISE - EXERCISE40videos
WORK, ENERGY AND POWER
- BOOK - AAKASH INSTITUTECHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - A)67videos
WORK, ENERGY AND POWER
- BOOK - AAKASH INSTITUTECHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-I (SUBJECTIVE TYPE QUESTIONS)6videos
WORK, ENERGY AND POWER
- BOOK - AAKASH INSTITUTECHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))12videos
WAVES
Similar Questions
A smooth of mass m1 is lying on a rigid horizontal string A bob of mass m2 hangs from, the ring by an inextensible light string of length l. Find angular frequency of oscillation of the system.
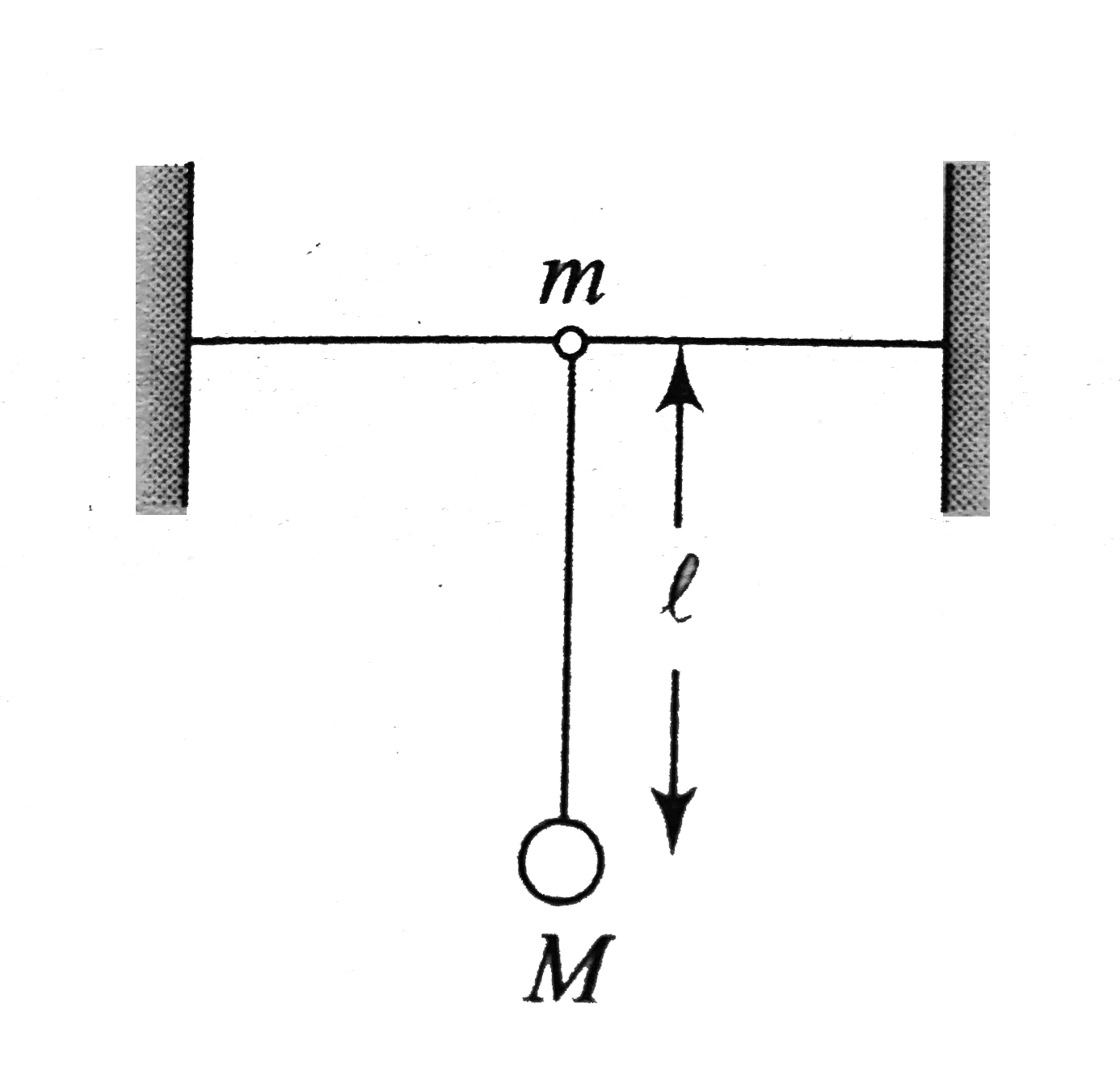 View Solution
View SolutionTwo small rings each of mass ‘m’ are connected to a block of same mass ‘m’ through inextensible light strings. Rings are constrained to move along a smooth horizontal rod. Initially system is held at rest (as shown in figure) with the strings just taut. Length of each string is ‘l’. The system is released from the position shown. Find the speed of the block (v) and speed of the rings (u) when the strings make an angle of theta=60^(@)withvertical.(Takeg = 10 m//s^2)
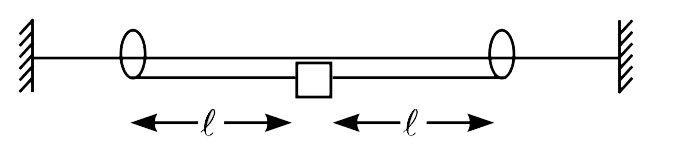 View Solution
View Solution
Knowledge Check
- Question 1 - Select One or More
Two masses m1 and m2 are connected by light inextensible string passing over a smooth pulley P. If the pulley moves vertically upwards with an acceleration equal to g then
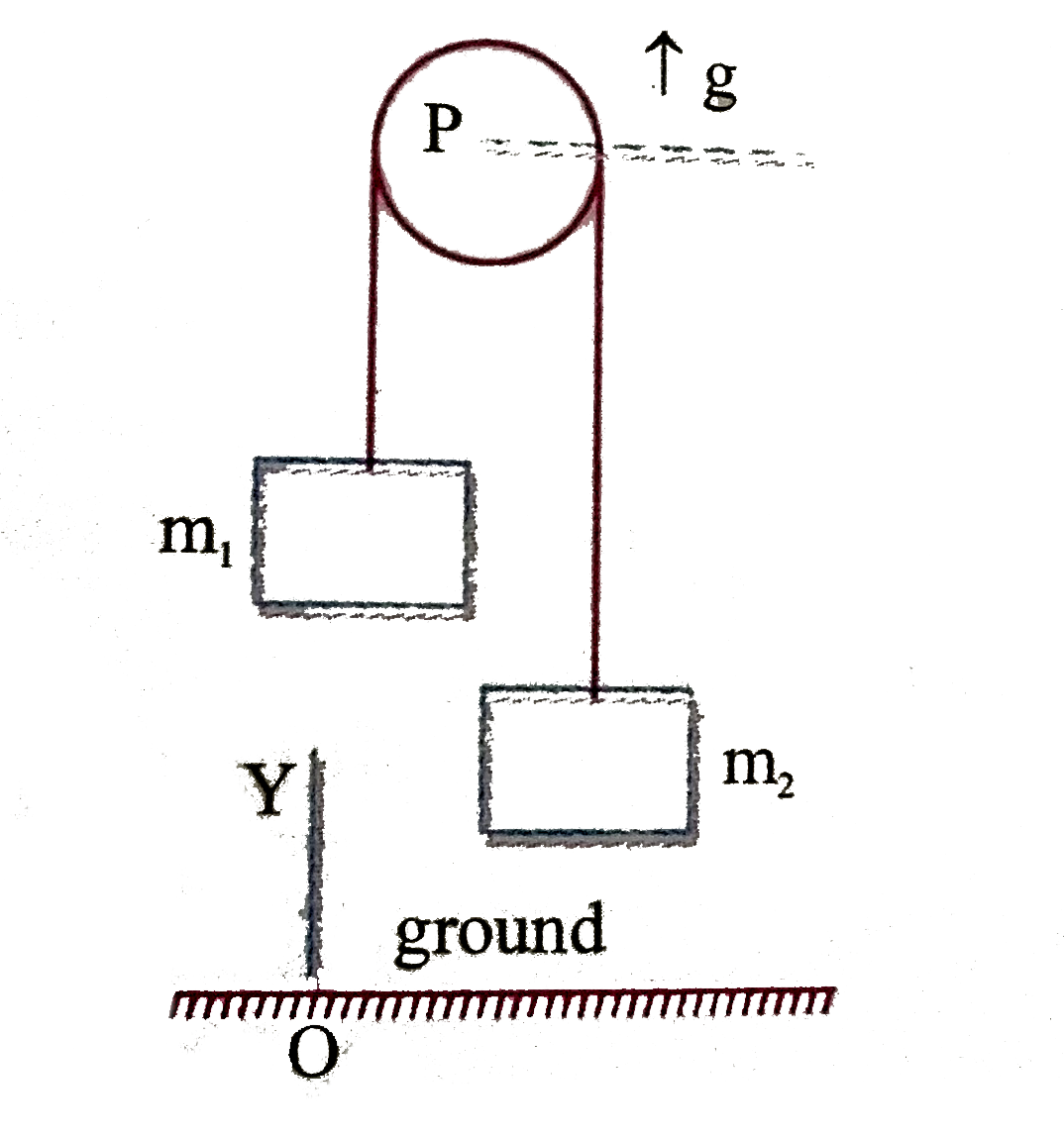 .ATension on the string is 4m1m2gm1+m2BTension on the string is 2m1m2gm1+m2CThe acceleration of mass m1 with respect to ground is 3m2−m1m1+m2g .DThe acceleration of mass m1 with respect to ground is 2(m2−m)m1+m2g
.ATension on the string is 4m1m2gm1+m2BTension on the string is 2m1m2gm1+m2CThe acceleration of mass m1 with respect to ground is 3m2−m1m1+m2g .DThe acceleration of mass m1 with respect to ground is 2(m2−m)m1+m2g - Question 2 - Select One
Two small rings each of mass 'm' are connected to a block of same mass 'm' through inextensible light strings. Rings are constrained to move along a smooth horizontal rod. Initially system is held at rest (as shown in figure) with the strings make an angle of θ=60∘ with vertical is. (Take g=10m/s2)
 A√3gl5B√gl5C√5gl4DNone of these
A√3gl5B√gl5C√5gl4DNone of these - Question 3 - Select One
A smooth ring of mass m can slide on a fixed horizontal rod. A string tied to the ring pases over a fixed pulley B and carries a block C of mass 2m as shown below. As the ring starts sliding
 AThe acceleration of the ring is 2gcosθ1+2cos2θBThe acceleration of the block is 2g1+2cos2θCThe tension in the string is 2mg1+2cos2θDIf the block descends with velocity v then the ring slides with velocity vcosθ
AThe acceleration of the ring is 2gcosθ1+2cos2θBThe acceleration of the block is 2g1+2cos2θCThe tension in the string is 2mg1+2cos2θDIf the block descends with velocity v then the ring slides with velocity vcosθ
Find the acceleration of masses m1 and m2 connected by an inextensible string, shown in figure-2.13(a). The string and pulley are assumed to be massless and frictionless.
View SolutionTwo block of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is:
 View Solution
View Solution
Two blocks of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is :View SolutionBlocks of mass M1 and M2 are connected by a cord which passes over the pulleys P1 and P2 as shown in the figure. If there is no friction, the acceleration of the block of mass M2 will be
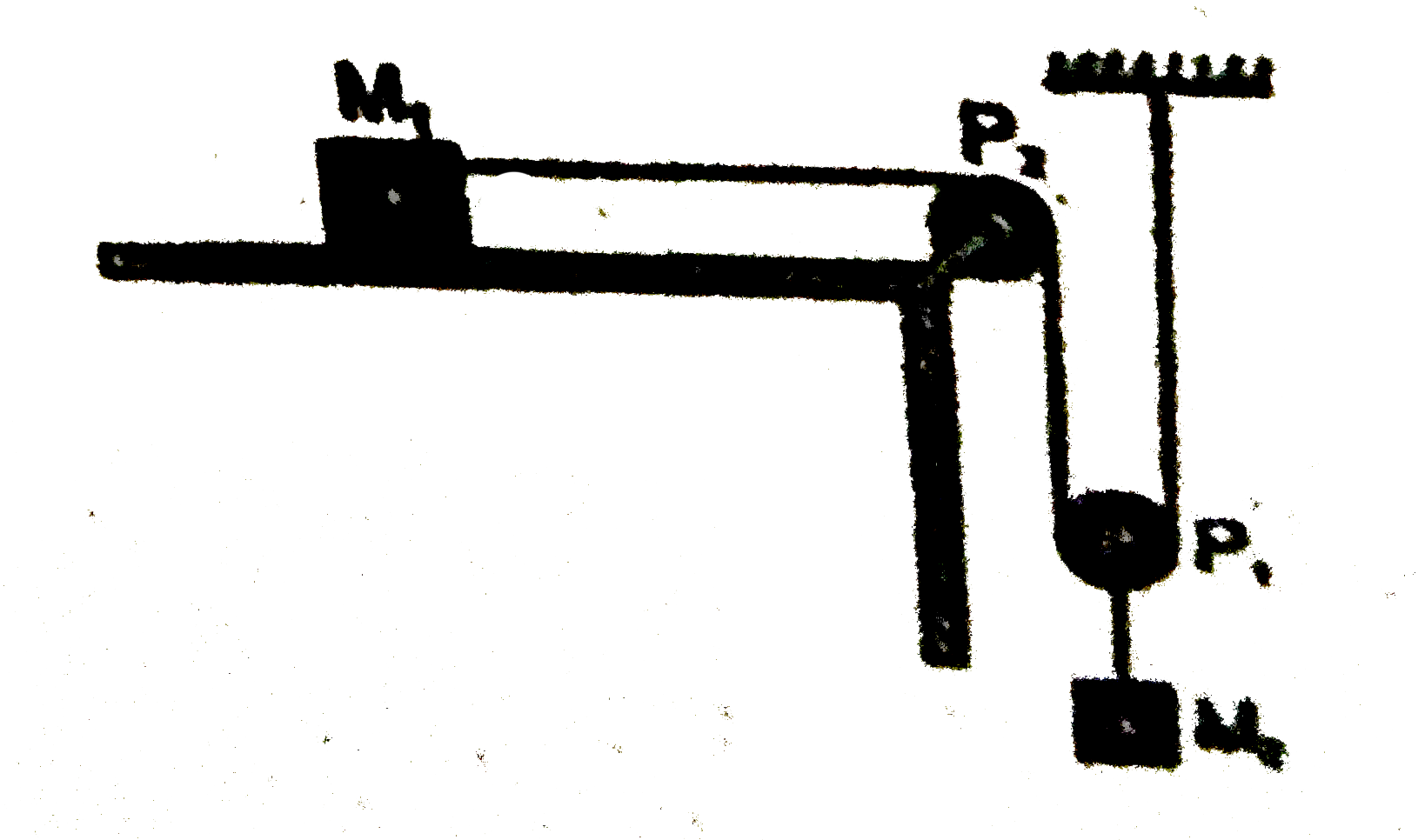 View Solution
View SolutionConsider the case of two bodies of masses m1andm2 which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations:
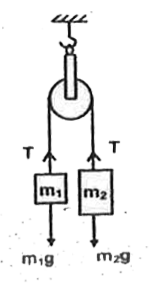
(i) when m1>m2. In this case
a=(m1−m2m1+m2)gandT=(2m1m2m1+m2)g
(ii) when m2>m1. In this case
a=(m2−m1m1+m2)gandT=(2m1m2m1+m2)g
(iii) When m1=m2=m. In this case a=0,T=mg
If the pulley is pulled upward with acceleration equal to the acceleration due to gravity, what will be the tension in the string?View Solution

