A pendulum bob swing from the point P when the ideal string of length l is horizontal. Find the
(A) Speed
(B) Acceleration of the bob
(C ) Power delivered by gravity at an angular position θ
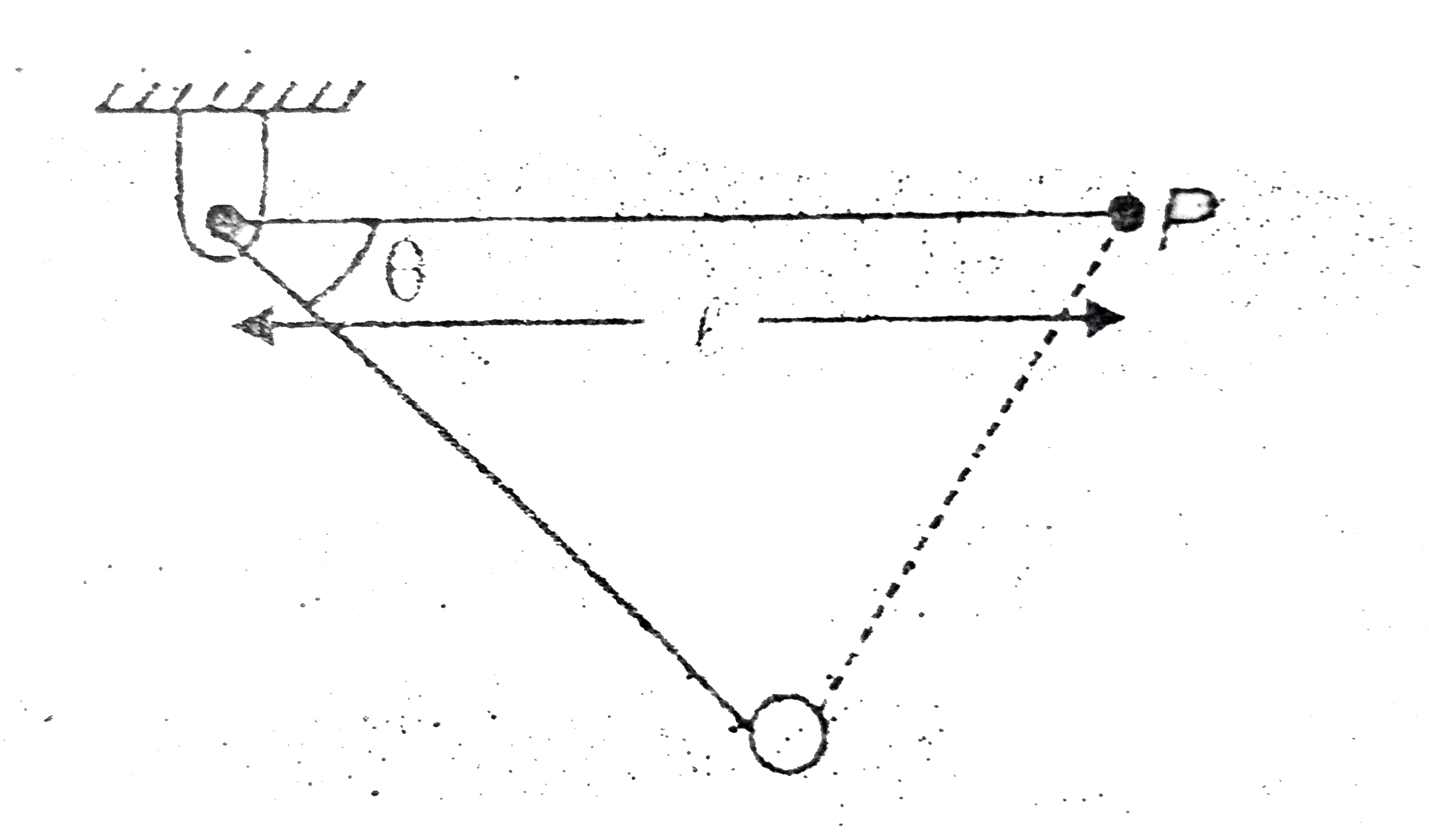
(A)v=√2glsinθ,
(B)θ=(√1+3sin2θg,
(C)mg(√2glsinθcosθ
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - WORK, ENERGY AND POWEREXERCISE - EXERCISE40videos
WORK, ENERGY AND POWER
- BOOK - AAKASH INSTITUTECHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - A)67videos
WORK, ENERGY AND POWER
- BOOK - AAKASH INSTITUTECHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-I (SUBJECTIVE TYPE QUESTIONS)6videos
WORK, ENERGY AND POWER
- BOOK - AAKASH INSTITUTECHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))12videos
WAVES
Similar Questions
Consider a conical pendulum having bob is mass m is suspended from a ceiling through a string of length L. The bob moves in a horizontal circle of radius r. Find (a) the angular speed of the bob and (b) the tension in the string.
 View Solution
View SolutionA coical pendulum consists of a string of length L whose upper end is fixed and another end is tied to a bob. The bob is moving in horizontal circle with constant angular speed ω such that the string makes a constant angle θ with the verticle. calculate time period T0 of revolution of bob in terms of L,g and θ.
View Solution
Knowledge Check
- Question 1 - Select One
A simple pendulum bob has a mass ''m'' and length ''L''. The bob is drawn aside such that the string is horizontal and then it is released. The velocity of the bob while it crosses the equilibrium position is
A√gLB√2gLC√5gLD√3gL - Question 2 - Select One
A simple pendulum is released from rest with the string in horizontal position. The vertical component of the velocity of the bob becomes maximum, when the string makes an angle θ with the vertical. The angle θ is equal to
Aπ4Bcos−1(1√3)Csin−1(1√3)Dπ3 - Question 3 - Select One
A pendulum bob is rotated in a vertical circle with one end of string of length l fixed at a position . At a certain instant bob is at its lowest position and is moving with speed u . Calculate the magnitude of change in velocity when string becomes horizontal for a moment .
A√(u2−gl)B√2(u2−gl)C√3(u2−gl)D2√(u2−gl)
(i) A simple pendulum consist of a small bob of mass m tied to a string of length L. Show that the total energy of oscillation of the pendulum is E≅12mgLθ20 when it is oscillating with a small angular amplitude θ0. Assume the gravitational potential energy to be zero of the lowest position of the bob. (ii) Three identical pendulums A, B and C are suspended from the ceiling of a room. They are swinging in semicircular arcs in vertical planes. The string of pendulum A snaps when it is vertical and it was found that the bob fell on the floor with speed V1. The string of B breaks when it makes an angle of 30° to the vertical and the bob hits the floor with speed V2. The string of pendulum C was cut when it was horizontal and the bob falls to the floor hitting it with a speed V3. Which is greatest and which is smallest among V1,V2 and V3?
View SolutionA simple pendulum is hanging from the roof of a trolley which is moving horizontally with acceleration g. If length of the string is L and mass of the bob is m, then time period of oscillation is
View SolutionA pendulum bob is projected form its lowest position with velocity (u), in horizontal direction, that is just enough to make the string horizontal (position OC). At angular position q, at point B, the speed (V) of the bob was observed to be half its initial projection speed (u).
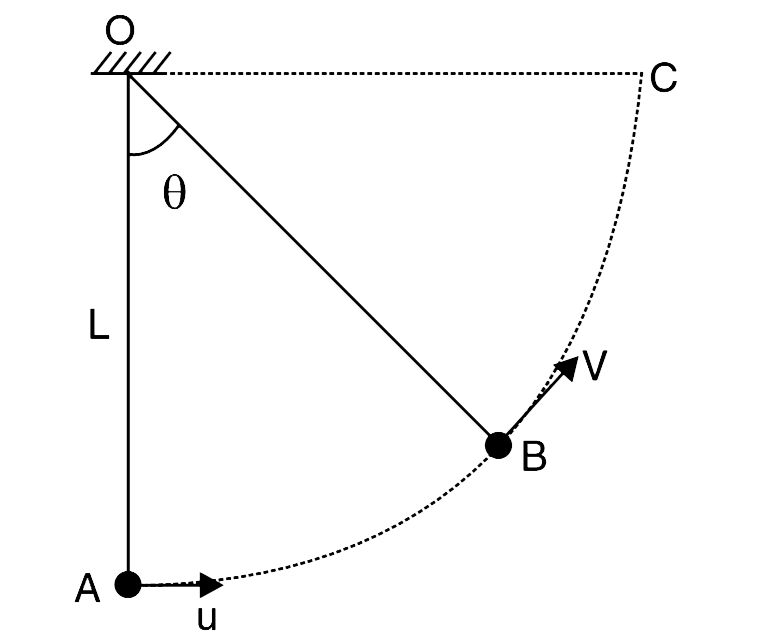
(a) Find θ
(b) Plot variation of magnitude of tangential acceleration of θ. (c) Let travel time from A to B be t1 and that from B to C be t2. Looking at the graph obtained in part (b), tell which is larger −t1 or t2 ?View SolutionA pendulum bob of mass m and length L is released from angle θ with the vertical. Find
(a) the speed of the bob at the bottom of the swing and
(b) tension in the string at that timeView SolutionBob of a simple pendulum of length L is projected horizontally with a speed of u=√4gh, , from the lowest position. Find the distance of the bob from vertical line AB, at the moment its tangential acceleration becomes zero.
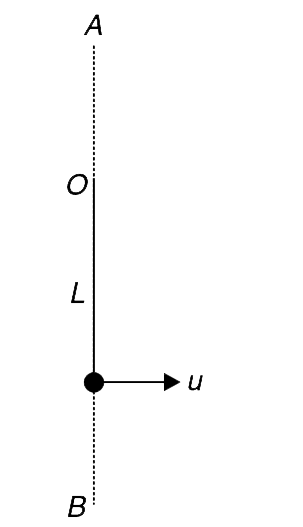 View Solution
View Solution

