A particle of mass $m$ has been thrown with intial speed $u$ making angle $θ$ with the horizontal ground. Find the angular momentum of the projectile about an axis perpendicular to the plane and passing through the point of projection when the projectile is
$(a)$ At the highest point
$(b)$ About to hit the ground

Video Solution

Text Solution

Verified by Experts

$(a)$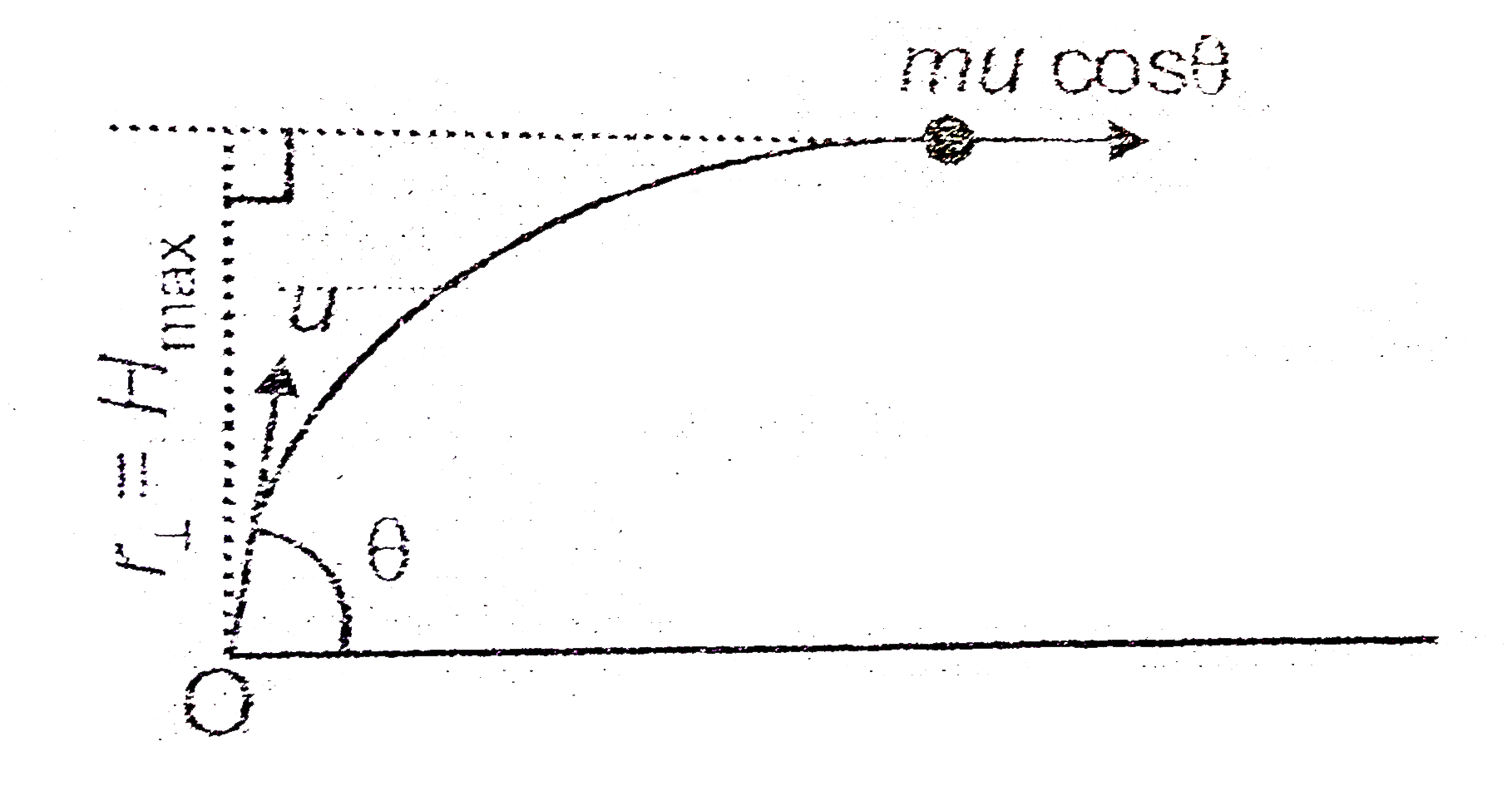
At the highest point the projectile has the momentum $μ cos θ$ in horizontal direction. Now, extend a line backward from the momentum direction and draw a perpendicular $r_{⊥}$ on it from $O$ . We can see $r_{⊥} = H_{max}$ . So angular momentum about $O$ is equal to $r_{⊥} \cdot μ cos θ = (H_{max}) μ cos θ$
$= \frac{u^{2} {sin}^{2} θ}{2 g} (μ cos θ)$ $⟨' H_{max} = \frac{u^{2} {sin}^{2} θ}{2 g})$
$= \frac{μ^{3} {sin}^{2} θ cos θ}{2 g}$
$(b)$ When the projectile is about to hit the ground the situation is as follows. Body will have momentum $μ$ at angle $θ$ with the horizontal just before hitting the ground.

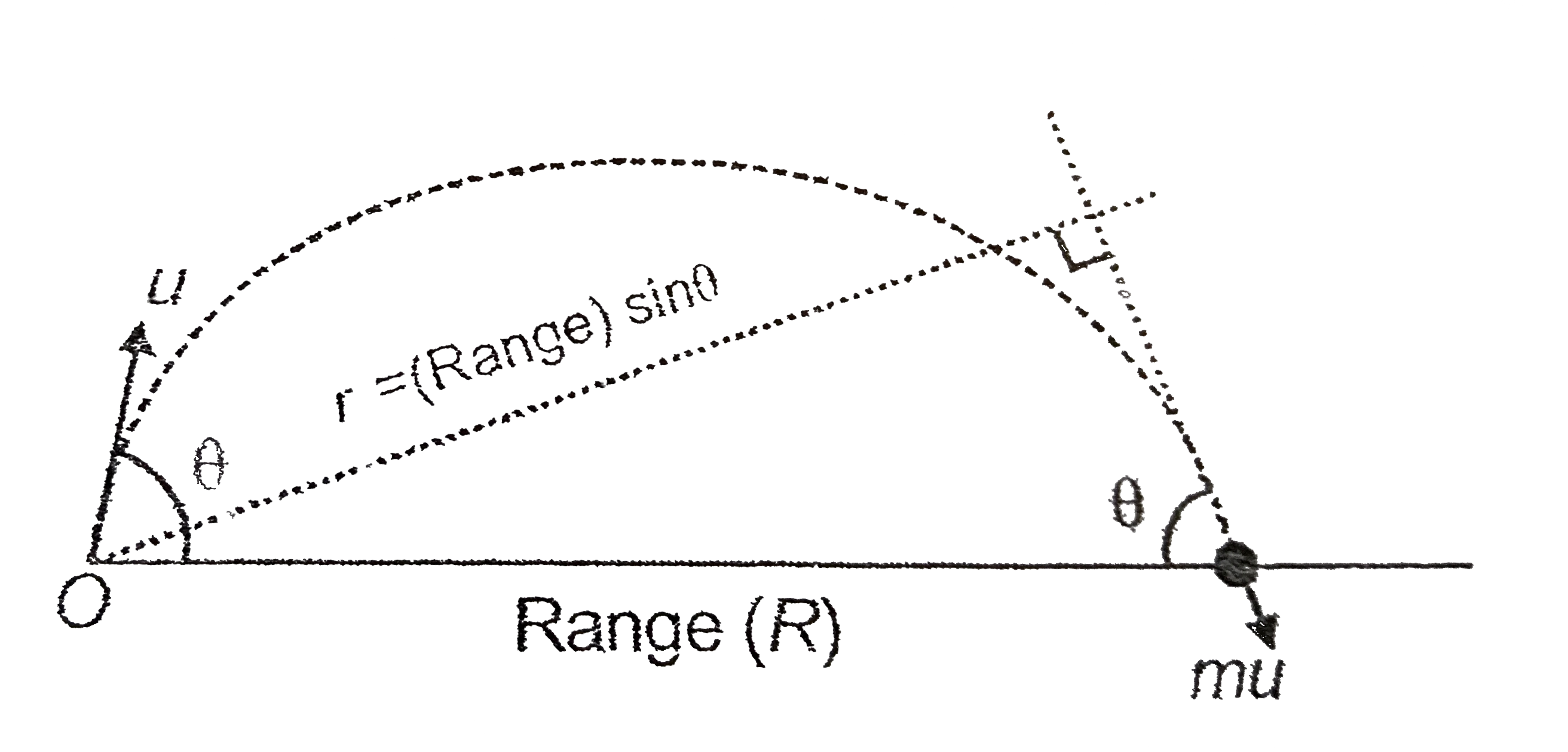
Now extend a line backward from momentum $μ$ and draw a perpendicular $r_{⊥}$ on it from $O$ . You can see $r_{⊥} = (Range) sin θ$
So, angular momentum about $O$ is equal to
$r_{⊥} \cdot μ = (Range) sin θ \cdot μ = (\frac{u^{2} sin 2 θ}{g}) sin θ \cdot μ$ $⟨' Range = \frac{u^{2} sin 2 θ}{g})$
$= (\frac{u^{2} 2 sin θ cos θ}{g}) sin θ \cdot μ$ $⟨' sin 2 θ = 2 sin θ cos θ)$
$= \frac{2 μ^{3} {sin}^{2} θ cos θ}{g}$

Updated on:21/07/2023

A particle of mass 1kg has been thrown with initial speed 20 $\frac{m}{s}$ making an angle 60° with the horizontal ground. the angular momentum of the particle about point of projection when the projectile is at highest point is (g=10m/s^2)
A $150 k g \frac{m^{2}}{s}$
B $300 k g \frac{m^{2}}{s}$
CZero
D $100 k g \frac{m^{2}}{s}$
A particle is fired from a point on the ground with speed $u$ making an angle $θ$ with the horizontal.Then
Athe radius of curvature of the projectile at the highest point is $\frac{u^{2} {cos}^{2} θ}{g}$
Bthe radius of curvature of the projectile at the highest point is $\frac{u^{2} {sin}^{2} θ}{g}$
Cat the point of projection magnitude of tangential acceleration is $g sin θ$
Dat the point of projection magnitude of tangential acceleration is $g cos θ$
A body of mass m is projected with intial speed u at an angle $θ$ with the horizontal. The change in momentum of body after time t is :-
Am u $sin θ$
B2 m u $sin θ$
Cm g t
Dzero