A square plate of side 'a' and mass 'm' is lying on a horizontal floor. A force F is applied at the top. Find the maximum force that can be applied on the square plate so that the plate does not topple about A.
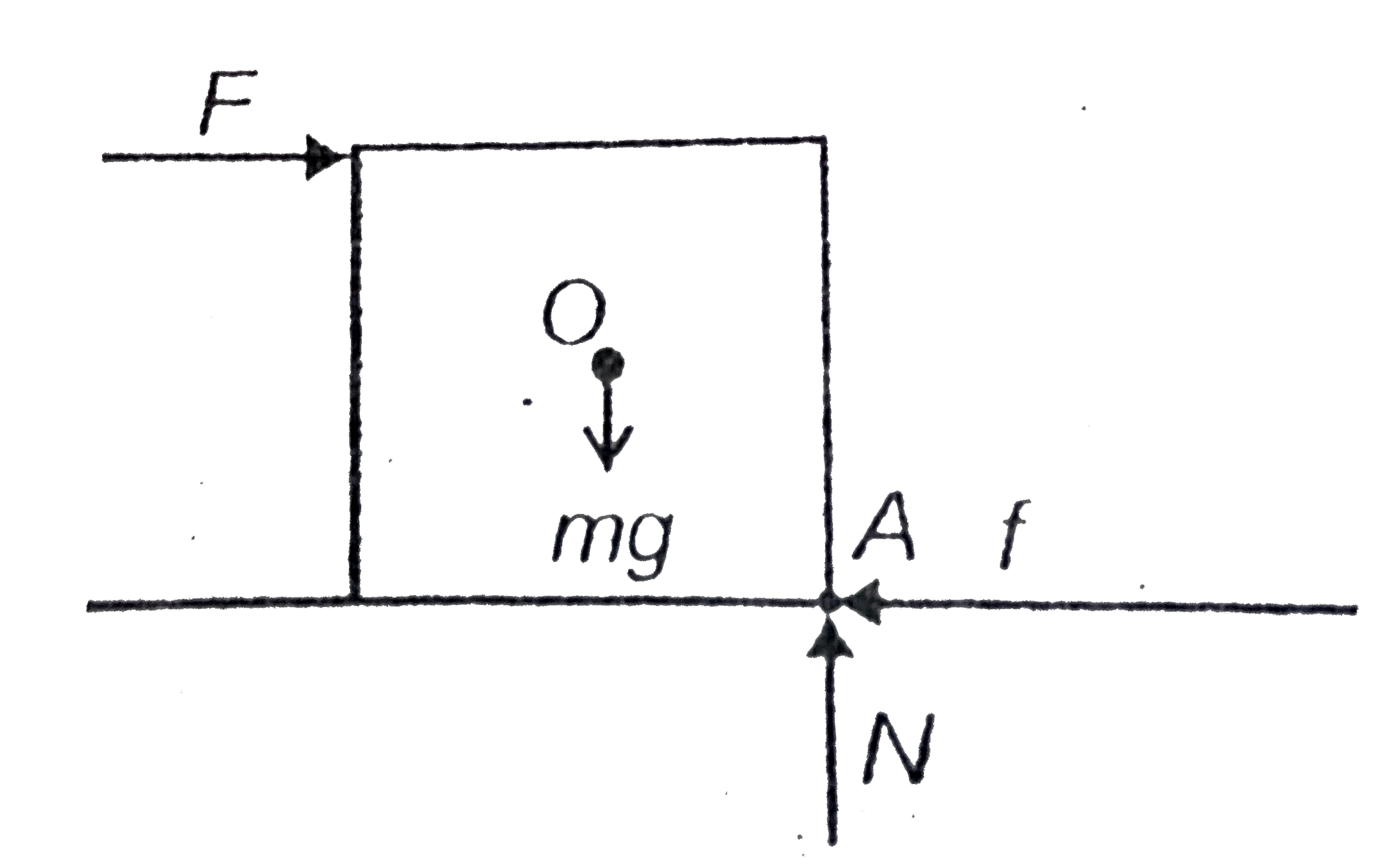
For force equilibrium
N=mg
f=F
For torque equilibrium
τ0=0=Fa2+f.a2−Na2
⇒Fa=mg.a2⇒F=mg2
Alternatively If a body is in complete equilibrium then net torque will be zero about all the points in the universe. So lets calculate the torque about point A.
Fa=mg.a2=−F=mg2
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - A) Objective Type Questions (One option is correct)62videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH INSTITUTECHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - B) Objective Type Questions (One option is correct)57videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH INSTITUTECHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Try Yourself63videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH INSTITUTECHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))5videos
SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITS
- BOOK - AAKASH INSTITUTECHAPTER - TEST 1EXERCISE - EXERCISE9videos
TEST 1
Similar Questions
12N of force required to be applied on A to slip on B. Find the maximum horizontal force F to be applied on B so that A and B moves together.
 View Solution
View SolutionA uniform cube of side 'a' and mass m rests on a rough horizontal table. A horizontal force F is applied normal to one of the faces at a point directly below the centre of the face, at a height a/4 above the base.
a. What is the minimum value of F for which the cube begins to tip about an edge?
b. What is the minimum value of its so that toppling occurs?
c. If μ=μmin find minimum force for topping.
d. Find minimum μs so that Fmin can cause toppling.View Solution
Knowledge Check
- Question 1 - Select One
A string of length L and mass M is lying on a horizontal table. A force F is applied at one of its ends. Tension in the string at a distance x from the end at which force is applied is
AZeroBFCF(L−y)LDF(l−y)M - Question 2 - Select One
A string of length L and mass M is lying on a horizontal table. A force F is applied at one of its ends. Tension in the string at a distance x from the end at which force is applied is
AZeroBF should be equal to the weight of A and BCF(L-x)/LDF(L-x)M - Question 3 - Select One
A square plate of side / has mass M. What is its moment of inertia about one of its diagonals ?
AMl26BMl212CMl23DMl24
A block of mass m rests on a horizontal floor for which coefficient of friction is μ . Find the magnitude and the direction of force that should be applied to just move the block so that the applied force is minimum.
View SolutionBlock B of mass m has been placed on block A of mass 3 m as shown. Block A rests on a smooth horizontal table. F1 is the maximum horizontal force that can be applied on the block A such that there is no slipping between the blocks. Similarly, F2 is the maximum horizontal force that can be applied on the block B so that the two blocks move together without slipping on each other. When F1andF2 both are applied together as shown in figure.

(a) Find the friction force acting between the blocks.
(b) Acceleration of the two blocks.
(c) If F2 is decreased a little, what will be direction of friction acting on B.View SolutionAn equilateral prism of mass m rests on a rough horizontal surface with coefficient of friction μ . A horizontal force F is applied on the top of prism as shown in figure. If the coefficient of friction is sufficiently high so that the prism does not slide before topping, the minimum force required to topple the prism is
 View Solution
View SolutionA square plate of side 15 cm. is floating on the surface of water. It the surface tension of water is 60 dyne/cm., the excess force applied to separate this plate from water will be
View SolutionAn equilateral prism of mass m rests on a rough horizontal surface with coefficient of friction μ. A horizontal force F is applied on the prism as shown in the figure. If the coefficient of friction is sufficiently high so that the prism does not slide before toppling, then the minimum force required to topple the prism is -
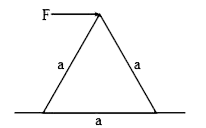 View Solution
View Solution

