Two masses m1 and m2 are joined with the help of massless string passing over a pulley of Radius R and mass M. Assume that string doesn't slip over the pulley. Take m1=10kg, m2=5kg, M=10kg, R=1m.

(a) Calculate the acceleration of each book.
(b) Calculate the tensions in the thread.
we choose m1, m2 and pulley as separate systems and draw their FBD.
(a) 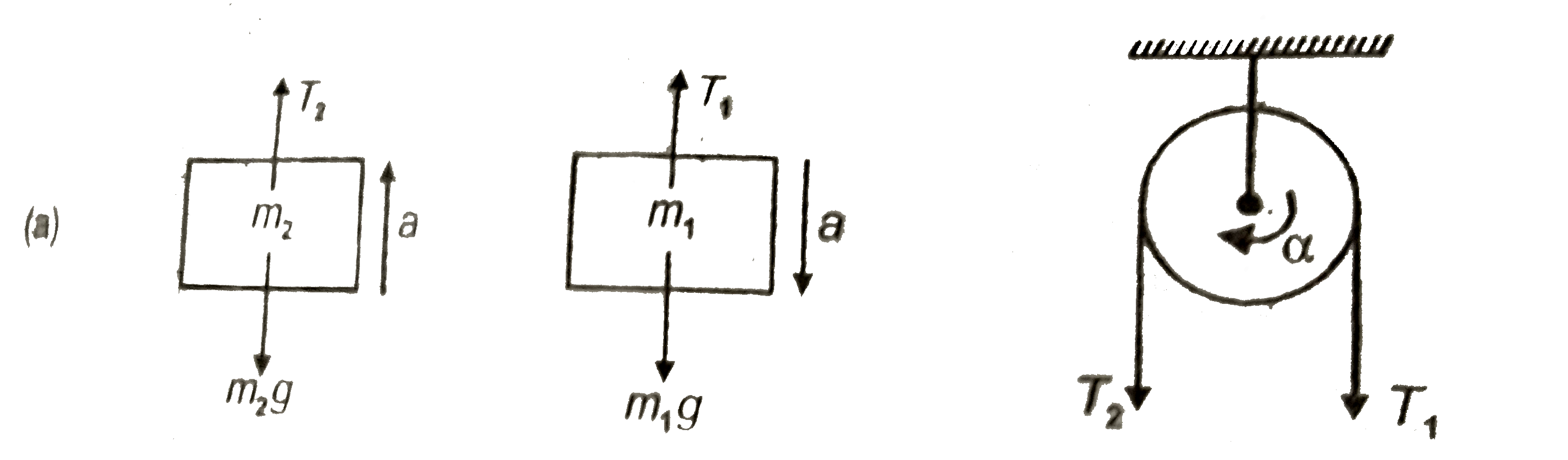
m1g−T1=m1a………(1) [from FBD of block of mass m1]
T2−m2g=m2a………..(2) [from FBD of block of mass m2]
T1R−R2R=lα [from FBD of the pulley]
⇒T1R−T2R=MR22α...........(3)
From equation (3) we can conculde that tension in a single thread will be different on two sides of the pulley, otherwise it will not be possible for the pulley to accelerate.
As we discussed in previous problem, the relation between the acceleration of the blocks and the angular acceleration of the pulley will be,
a=αR..........(4)
Using equation (1), (2), (3) & (4), we get
m1g−T1=m1a
T2−m2g=m2a
T1−T2=Ma2(m1−m2)g=(m1+m2+M2)a (adding all the equations)
⇒a=(m1−m2)g(m1+m2+M2)
⇒a=5015+5=2.5m/s2
(b) Tensions T1=m1g−m1a
=m1(g−a)
=10(10−2.5)
=75N
T2=m2(g+a)
=5(10+2.5)
=62.5N.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Illustration4videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH INSTITUTECHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - A) Objective Type Questions (One option is correct)62videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH INSTITUTECHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))5videos
SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITS
- BOOK - AAKASH INSTITUTECHAPTER - TEST 1EXERCISE - EXERCISE9videos
TEST 1
Similar Questions
Two masses 2m and m are attached to the ends of the card which passes over a pulley of mass m and radius R. Calculate the tension in the wire on both sides of the pulley. Assume no slipping.
View SolutionTwo blocks of masses m1andm2(m1>m2) connected by a massless string passing over a frictionless pulley Magnitude of acceleration of blocks would be
View Solution
Knowledge Check
- Question 1 - Select One or More
Two masses M and m(M>m) are joined by a light string passing over a smooth light pulley.
 AThe acceleration of each block is (M−mM+m)gBThe tension in the string is 2MmgM+mCThe centre of mass of the 'M plus m' system moves down with an acceleration of g(M−mM+m)2DThe tension in the string by which the pulley is attached to the rodd is (M+m)g
AThe acceleration of each block is (M−mM+m)gBThe tension in the string is 2MmgM+mCThe centre of mass of the 'M plus m' system moves down with an acceleration of g(M−mM+m)2DThe tension in the string by which the pulley is attached to the rodd is (M+m)g - Question 2 - Select One or More
Two masses m and M(m<M) are joined by a light string passing over a smooth and light pulley (as shown)
 Athe acceleration of each mass is (M−mM+m)gBthe tension in the string connecting masses is (2MmM+m)gCthe thrust acting on the pulley is (4MmM+m)gDNone of the above
Athe acceleration of each mass is (M−mM+m)gBthe tension in the string connecting masses is (2MmM+m)gCthe thrust acting on the pulley is (4MmM+m)gDNone of the above - Question 3 - Select One
Two masses m1 and m2 are connected to the ends of a massless string that passes over a pulley fixed at the top of a double incline as shown. Assuming m1>m2 acceleration of the system is:
 Am1gsinθ1+m2gsinθ2m1+m2Bm1gsinθ1−m2gsinθ2m1−m2Cm1gsinθ1−m2gsinθ2m1+m2D(m1+m2)(sinθ1+sinθ2)gm1−m2
Am1gsinθ1+m2gsinθ2m1+m2Bm1gsinθ1−m2gsinθ2m1−m2Cm1gsinθ1−m2gsinθ2m1+m2D(m1+m2)(sinθ1+sinθ2)gm1−m2
Two masses m and M(>m) are joined by a light string passing over a smooth light pulley. The centre of mass of the system moves with an acceleration
 View Solution
View SolutionTwo masses ,each equal to m ,are arrached to one another by a massless string passing over a smooth pulley the tension in the string is :
View SolutionTwo masses m1 and m2 are attached to the ends of a massless string which passes over a frictionless pulley attached to the top of an inclined plane. The angle of inclination of the plane is θ. Take g=10ms−2
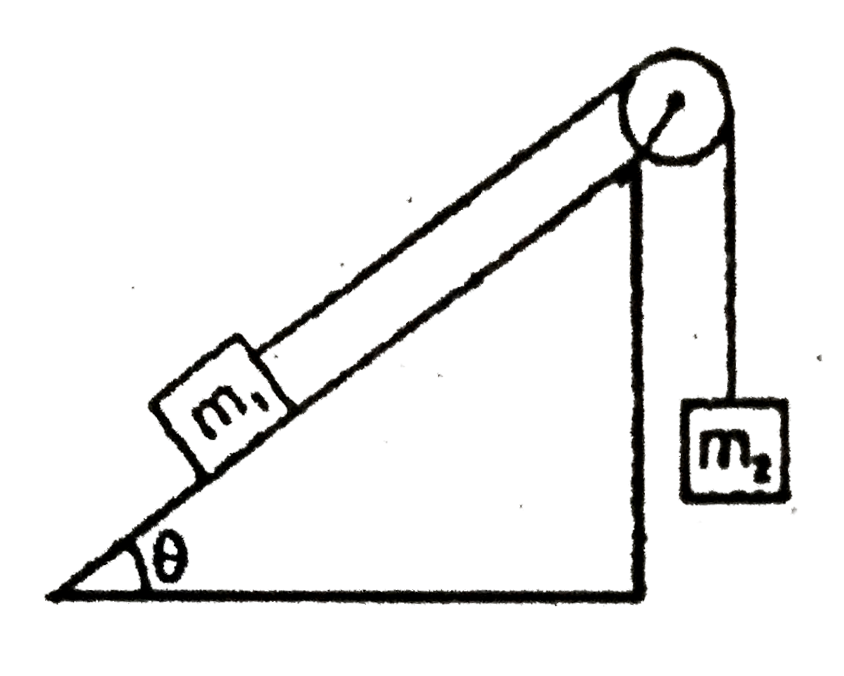
if m1=10kg,m2=5kg,θ=30∘, what is the acceleration of mass m2?View SolutionTwo masses 2 kg and 3 kg are attached to the end of the string passed over a pulley fixed at the top. The tension and acceleration are
View SolutionTwo masses M1=5kg,M2=10kg are connected at the ends of an inextensible string passing over a frictionless pulley as shown. When masses are released, then acceleration of masses will be
 View Solution
View Solution

