Two masses 2kg and 5kg are placed at points 'A' and 'B' as shown in the figure
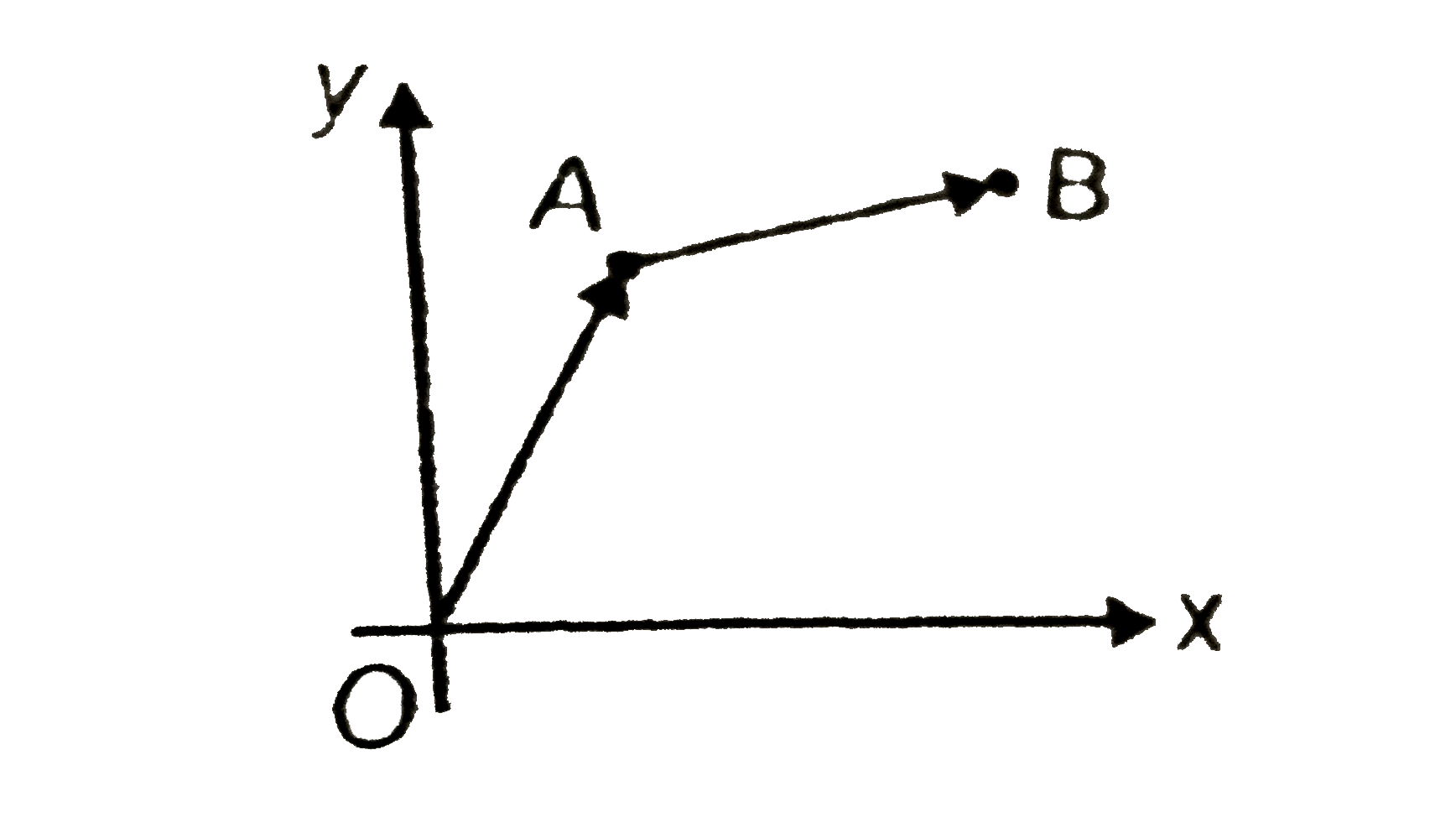
→OA=2ˆi+3ˆj
→AB=5ˆi+8ˆj
Find the co-ordinates of centre of mass.
A
(397,617)
B
(367,587)
C
(397,637)
D
(297,617)
Video Solution
|
Answer
Step by step video & image solution for Two masses 2kg and 5kg are placed at points 'A' and 'B' as shown in the figure vecOA=2hati+3hatj vecAB=5hati+8hatj Find the co-ordinates of centre of mass. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTECHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - C) Objective Type Questions (More than one option are correct)
28 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTECHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - D) Linked Comprehension Type Questions
20 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTECHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - A) Objective Type Questions (One option is correct)
62 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - AAKASH INSTITUTECHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))
5 Videos
- TEST 1BOOK - AAKASH INSTITUTECHAPTER - TEST 1EXERCISE - EXERCISE
9 Videos
Similar Questions
Knowledge Check
The two vectors A=2ˆi+ˆj+3ˆk and B=7ˆi−5ˆj−3ˆk are -
AparallelBperpendicularCanti-parallelDnone of theseif a=2ˆi+ˆj+2ˆtkandb=5ˆi−3ˆj+ˆk, then the projection of 'b' and 'a' is
A3B4C5D6Three bodies of masses 3kg, 2kg and 1 kg kept at points (3ˆi+2ˆj),(5ˆj+ˆk) and (2ˆi+ˆk) respectively. Then the position vector of their centre of mass is given by
A→Rcm=11ˆi6+38ˆj+2ˆkB→Rcm=11ˆi6+83ˆj+ˆk2C→Rcm=7ˆi6+58ˆj+2ˆkD→RCM=11ˆi6+85ˆj+3ˆk
Find the components of a vector →A=2ˆi+3ˆj along the directions of ˆi+ˆj and ˆi−ˆj
View SolutionFind the scalar product of vectors →a=2ˆi−ˆj+2ˆkand→b=ˆi−3ˆj−5ˆk
View SolutionFind the components of →a=2ˆi+3ˆj along the direction of vectors ˆi+ˆj and ˆi−ˆj.
View SolutionIf the points with position vectors 60ˆi+3ˆj,40ˆi−8ˆjandaˆi−52ˆj are collinear, then a =
View SolutionThe angle between the two vectors A=3ˆi+4ˆj+5ˆk and B=3ˆi+ˆj−5ˆk is
View Solution
