A body of mass m is projected from ground for horizontal range R. At the highest point it is fragmented into two identical parts. If one parts returns back to the point of projection, then other part will have the horizontal range
R
3R2
2R
52R
To solve the problem step by step, we will analyze the motion of the body and apply the principles of conservation of momentum and projectile motion.
Step 1: Understanding the Initial Conditions
A body of mass m is projected at an angle θ with an initial velocity u. The horizontal range R can be expressed using the formula:
\(
R = \frac{u^2 \sin 2\theta}{g}
\)
where g is the acceleration due to gravity.
Hint: Remember the formula for the range of a projectile and the significance of the angle of projection.
Step 2: Analyzing the Fragmentation
At the highest point of its trajectory, the body is fragmented into two identical parts, each of mass m2. One part (let's call it m1) returns to the point of projection, while the other part (let's call it m2) continues to move horizontally.
Hint: Identify that at the highest point, the vertical component of the velocity is zero, and only the horizontal component remains.
Step 3: Applying Conservation of Momentum
Since no external horizontal forces act on the system, we can apply the conservation of linear momentum in the horizontal direction. Let b1 be the velocity of m1 (which returns to the projection point) and b2 be the velocity of m2.
The initial momentum (before fragmentation) is:
\(
P_{\text{initial}} = m \cdot u \cos \theta
\)
After fragmentation, the momentum is:
\(
P_{\text{final}} = \frac{m}{2} (-b1) + \frac{m}{2} b2
\)
Setting the initial momentum equal to the final momentum gives:
\(
m \cdot u \cos \theta = \frac{m}{2} (-b1) + \frac{m}{2} b2
\)
Hint: Remember that b1 is negative because it is in the opposite direction to the initial motion.
Step 4: Solving for Velocities
From the conservation of momentum equation, we can simplify:
\(
u \cos \theta = -\frac{1}{2} b1 + \frac{1}{2} b2
\)
Multiplying through by 2:
\(
2u \cos \theta = -b1 + b2
\)
Rearranging gives:
\(
b2 = 2u \cos \theta + b1
\)
Hint: Keep track of the signs of the velocities based on their directions.
Step 5: Finding the Velocity of m1
When m1 returns to the projection point, it travels a horizontal distance of R2. The time taken to return can be expressed as:
\(
t_0 = \frac{R/2}{b1}
\)
Using the range formula, we can express R in terms of u and θ:
\(
t_0 = \frac{u^2 \sin 2\theta}{2g \cdot b1}
\)
Hint: Relate the time of flight to the horizontal distance covered.
Step 6: Finding the Velocity of m2
Using the previously derived expression for b2, we substitute b1 to find b2:
\(
b2 = 2u \cos \theta + b1
\)
Step 7: Calculating the Range of m2
The range of m2 can be calculated using the time of flight and its horizontal velocity b2:
\(
\text{Range of } m2 = b2 \cdot t_{\text{flight}}
\)
Where tflight is the time taken to reach the ground from the maximum height.
Hint: Use the vertical motion equations to determine the time of flight for m2.
Step 8: Final Calculation
After substituting the values and simplifying, we find that the range of m2 is:
\(
\text{Range of } m2 = \frac{3}{2} R
\)
Conclusion
Thus, the other part (m2) will have a horizontal range of:
\(
\frac{3R}{2}
\)
Final Answer: The horizontal range of the other part will be \( \frac{3R}{2} \).
A body of mass m is projected at an angle θ with an initial velocity u. The horizontal range R can be expressed using the formula:
\(
R = \frac{u^2 \sin 2\theta}{g}
\)
where g is the acceleration due to gravity.
At the highest point of its trajectory, the body is fragmented into two identical parts, each of mass m2. One part (let's call it m1) returns to the point of projection, while the other part (let's call it m2) continues to move horizontally.
Since no external horizontal forces act on the system, we can apply the conservation of linear momentum in the horizontal direction. Let b1 be the velocity of m1 (which returns to the projection point) and b2 be the velocity of m2.
\(
P_{\text{initial}} = m \cdot u \cos \theta
\)
\(
P_{\text{final}} = \frac{m}{2} (-b1) + \frac{m}{2} b2
\)
Setting the initial momentum equal to the final momentum gives:
\(
m \cdot u \cos \theta = \frac{m}{2} (-b1) + \frac{m}{2} b2
\)
From the conservation of momentum equation, we can simplify:
\(
u \cos \theta = -\frac{1}{2} b1 + \frac{1}{2} b2
\)
Multiplying through by 2:
\(
2u \cos \theta = -b1 + b2
\)
Rearranging gives:
\(
b2 = 2u \cos \theta + b1
\)
When m1 returns to the projection point, it travels a horizontal distance of R2. The time taken to return can be expressed as:
\(
t_0 = \frac{R/2}{b1}
\)
Using the range formula, we can express R in terms of u and θ:
\(
t_0 = \frac{u^2 \sin 2\theta}{2g \cdot b1}
\)
Using the previously derived expression for b2, we substitute b1 to find b2:
\(
b2 = 2u \cos \theta + b1
\)
The range of m2 can be calculated using the time of flight and its horizontal velocity b2:
\(
\text{Range of } m2 = b2 \cdot t_{\text{flight}}
\)
Where tflight is the time taken to reach the ground from the maximum height.
After substituting the values and simplifying, we find that the range of m2 is:
\(
\text{Range of } m2 = \frac{3}{2} R
\)
Thus, the other part (m2) will have a horizontal range of:
\(
\frac{3R}{2}
\)
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBook:AAKASH INSTITUTEChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONExercise:Assignment (Section - C) Objective Type Questions (More than one option are correct)
Explore 28 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBook:AAKASH INSTITUTEChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONExercise:Assignment (Section - D) Linked Comprehension Type Questions
Explore 20 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBook:AAKASH INSTITUTEChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONExercise:Assignment (Section - A) Objective Type Questions (One option is correct)
Explore 62 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBook:AAKASH INSTITUTEChapter:SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSExercise:Assignment (Section-D (Assertion and reason))
Explore 5 Videos
- TEST 1Book:AAKASH INSTITUTEChapter:TEST 1Exercise:EXERCISE
Explore 9 Videos
Similar Questions
A projectile of mass 5m is projected at 40m/s at 75^(@) above horizontal It explodes at highest point into two fragments The smaller part of mass m falls at the point of projection.Where does the other part fall? (distance from point of projection) (A) 60m (B) 40m (C) 100m (D) 80m
View SolutionA projectile of mass 5m is projected at 40m/s at 75^(@) above horizontal It explodes at highest point into two fragments The smaller part of mass m falls at the point of projection.Where does the other part fall? (distance from point of projection) (A) 60m (B)40m (C)100 (D)80
View Solution
Knowledge Check
In figure, the angle of elevation of the top of a tower AC from a point B on the ground is 60∘. If the height of the tower is 20m , find the distance of the point from the foot of the tower.
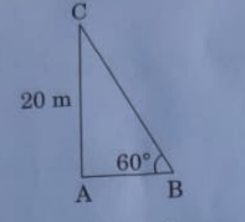 A200mB250mC150mD50m
A200mB250mC150mD50mA particle is projected such that its horizontal range would be R. At the highest point, the particle breaks into two identical parts P and Q. If P comes to rest, the horizontal distance of point from the point of projection (i.e. origin) where the particle Q lands on the ground is
A1.5 RBRC2.5 RD2 RA particle of mass 4m is projected from the ground at some angle with horizontal. Its horizontal range is R. At the highest point of its path it breaks into two pieces of masses m and 3m, respectively, such that the smaller mass comes to rest. The larger mass finally falls at a distance x from the point of projection, where x is equal to
A2R3B7R6C5R4Dnone of these
Show that there are two angles of projection for which the horizontal range is the same.
View SolutionA body is thrown from ground for horizontal range 100 m. If the body breaks into two fragments of mass in the ratio 1:2 at the highest point and smaller mass stops there and comes vertically downward, then horizontal range of the centre of mass of the body is
View SolutionA body is projected at angle of 45∘ to the horizontal . What is its velocity at the highest point ?
View SolutionA particle of mass 3m is projected from the ground at some angle with horizontal. Its horizontal range is R. At the highest point of its path it breaks into two pieces of masses m and 2m respectively. The smallar mass comes to rest. The larger mass finally falls at a distance x from the point of projection where x is equal to
View SolutionA particle of mass 3m is projected from the ground at some angle with horizontal. Its horizontal range is R. At the highest point of its path it breaks into two pieces of masses m and 2m respectively. The smallar mass comes to rest. The larger mass finally falls at a distance x from the point of projection where x is equal to
View Solution