A particle of mass m strikes a disc of radius R and mass m with a speed u as shown in the figure. What is the speed of the particle just after the collision if the collision is perfectly inelastic ?
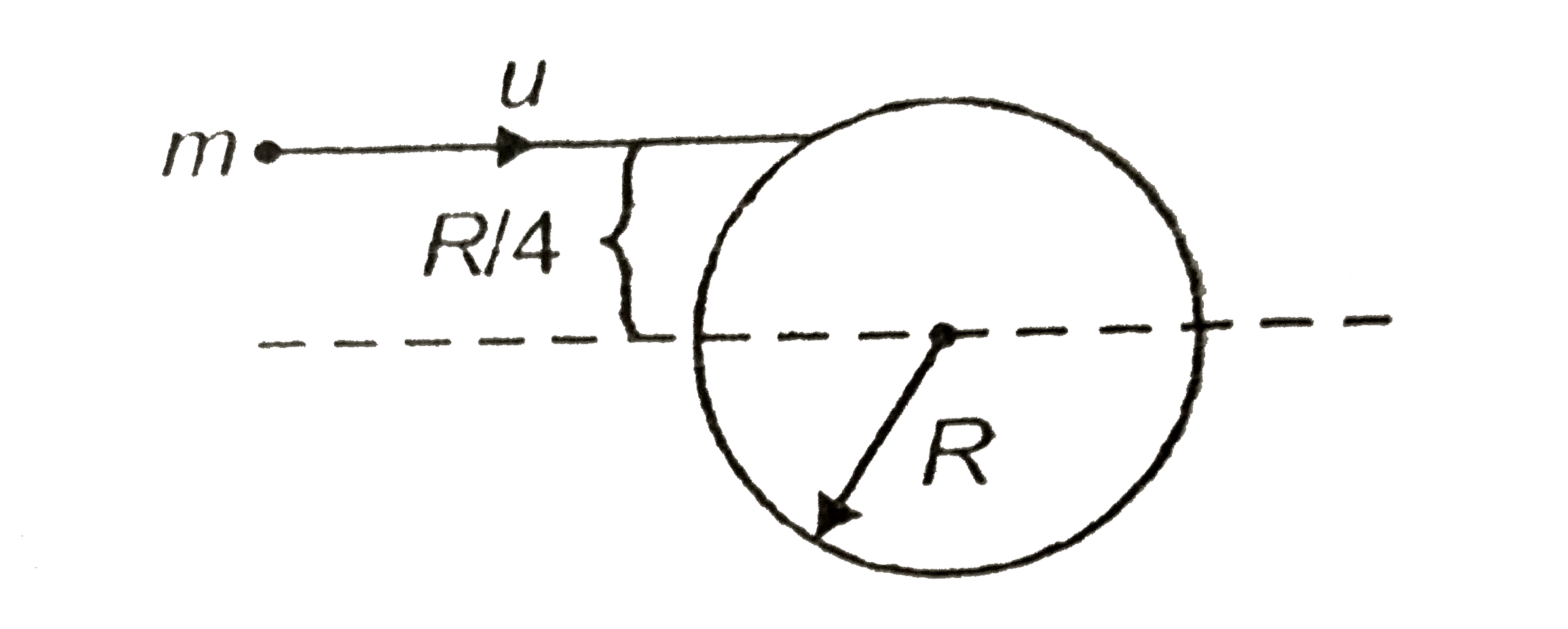
u√214
u√194
u√198
u√218
Step by step video & image solution for A particle of mass m strikes a disc of radius R and mass m with a speed u as shown in the figure. What is the speed of the particle just after the collision if the collision is perfectly inelastic ? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTECHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - C) Objective Type Questions (More than one option are correct)
28 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTECHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - D) Linked Comprehension Type Questions
20 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTECHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - A) Objective Type Questions (One option is correct)
62 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - AAKASH INSTITUTECHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))
5 Videos
- TEST 1BOOK - AAKASH INSTITUTECHAPTER - TEST 1EXERCISE - EXERCISE
9 Videos
Similar Questions
A particle of mass m strikes elastically with a disc of radius R, with a velocity →v as shown in the figure. If the mass of the disc is equal to that of the particle and the surface of the contact is smooth, find the velocity of the disc just after the collision.

View SolutionA particle of mass m strikes another particle of same at rest. Find the angle between velocities of particles after the collision , if the collision is elastic.
View Solution
Knowledge Check
A particle of mass m moving with horizontal speed 6m/s as shown in the figure. If m<<M then for one - dimensional elastic collision , the speed of lighter particle after collision will be
 A2m/sec in original directionB2 m/sec opposite to the original directionC4 m/sec opposite to the original directionD4 m/sec in original direction
A2m/sec in original directionB2 m/sec opposite to the original directionC4 m/sec opposite to the original directionD4 m/sec in original directionA particle of mass m moving with horizontal speed 6m/s as shown in the figure. If m<<M then for one - dimensional elastic collision , the speed of lighter particle after collision will be
 A2m/s in original directionB2m/s opposite to the original directionC4m/s opposite to the original directionD4m/s in original direction
A2m/s in original directionB2m/s opposite to the original directionC4m/s opposite to the original directionD4m/s in original directionTwo particle of masses m and 2m are coliding elastically as given in figure. If V1 and V2 speed of particle just after collision then
_2019_CBT5_E01_051_Q01.png) AV1=11.16m/s,V2=6.31m/sBV1=10.16m/s,V2=5.31m/sCv1=9.16M/S,v2=6.31M/SDv1=6.31M/S,v2=11.16M/S
AV1=11.16m/s,V2=6.31m/sBV1=10.16m/s,V2=5.31m/sCv1=9.16M/S,v2=6.31M/SDv1=6.31M/S,v2=11.16M/S
Two particles A and B of mass 3kg and 2kg moving with speed 10m/s and 5m/s as shown in figure.
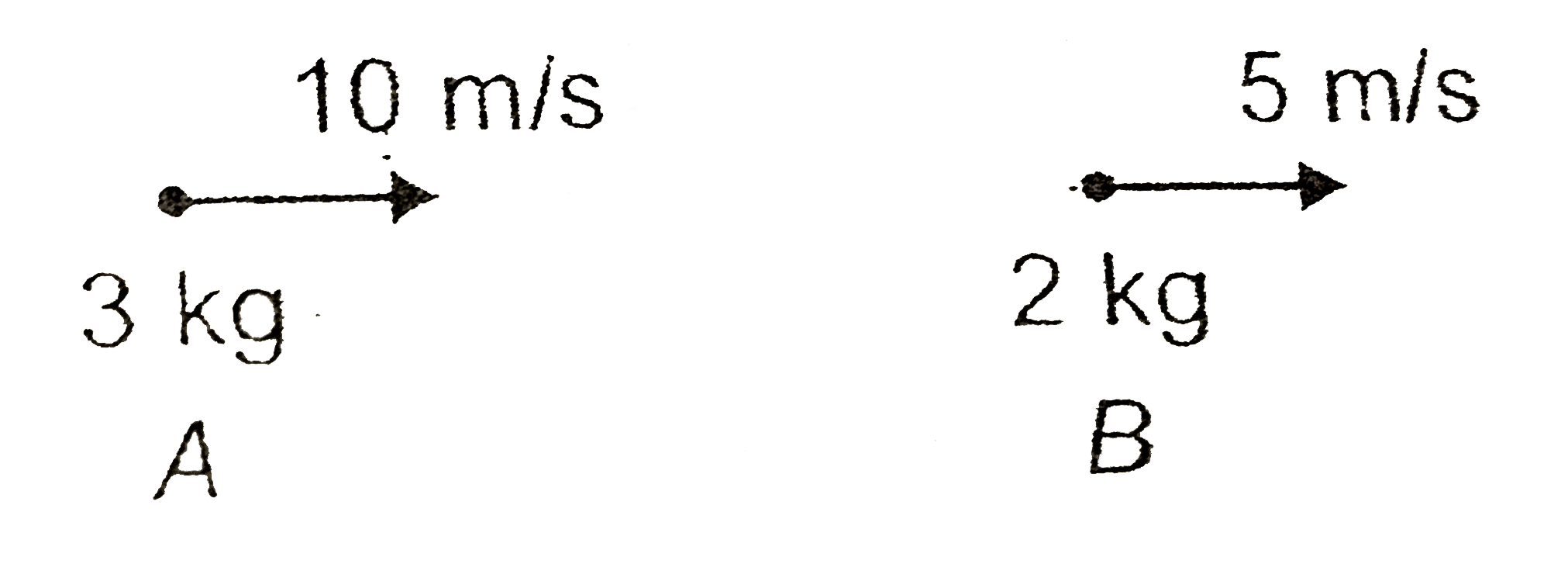
Find the maximum momentum that particle B can have after collision with B.
View SolutionTwo particles A and B of mass 3kg and 2kg moving with speed 10m/s and 5m/s as shown in figure.
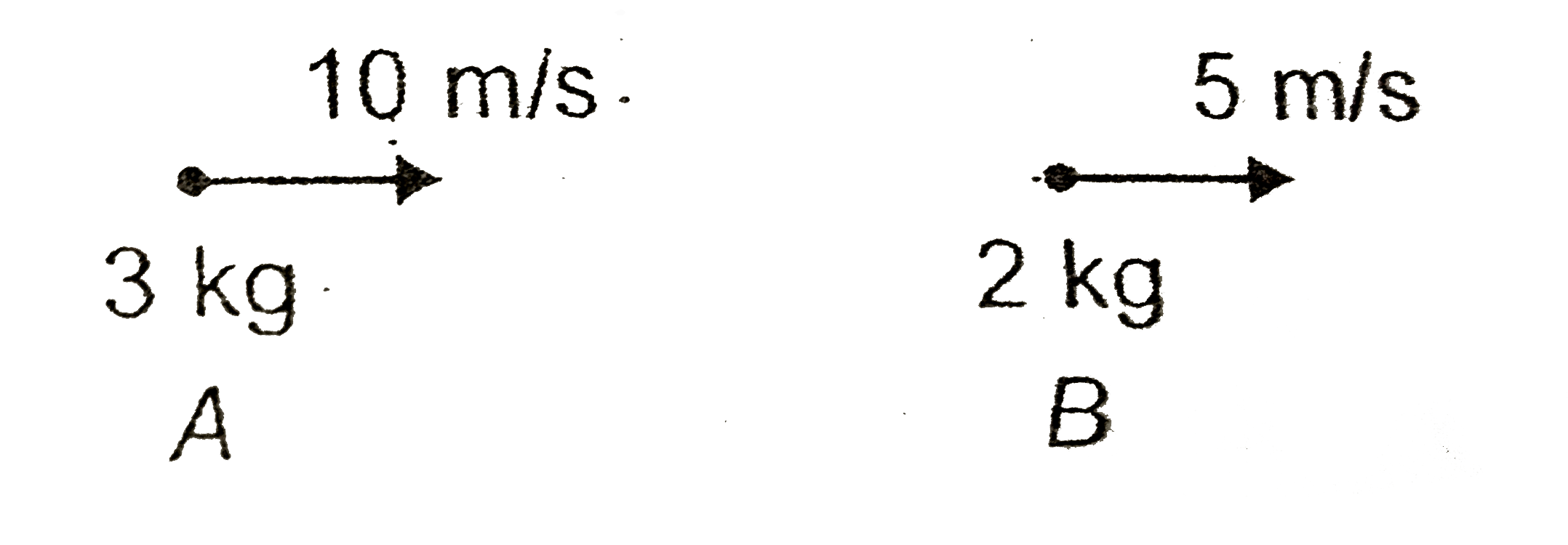
Find the maximum momentum that particles A can have after collision with B.
View SolutionA particle (a mud pallet, say) of mass m strikes a smooth stationary wedge of mass M with as velocity v0 at an angle θ with horizontal. If the collision is perfectly inelastic, find the
a. velocity of the wedge just after the collision.
b. Chane in KE of the system (M+m) in collision.
View SolutionA particle of mass m collides with a uniform rod of mass M and length L as shown in figure. If initial speed of the particle was u. Find the final velocity vector of the rod and particle just after collision.(The complete system is in horizontal plane)
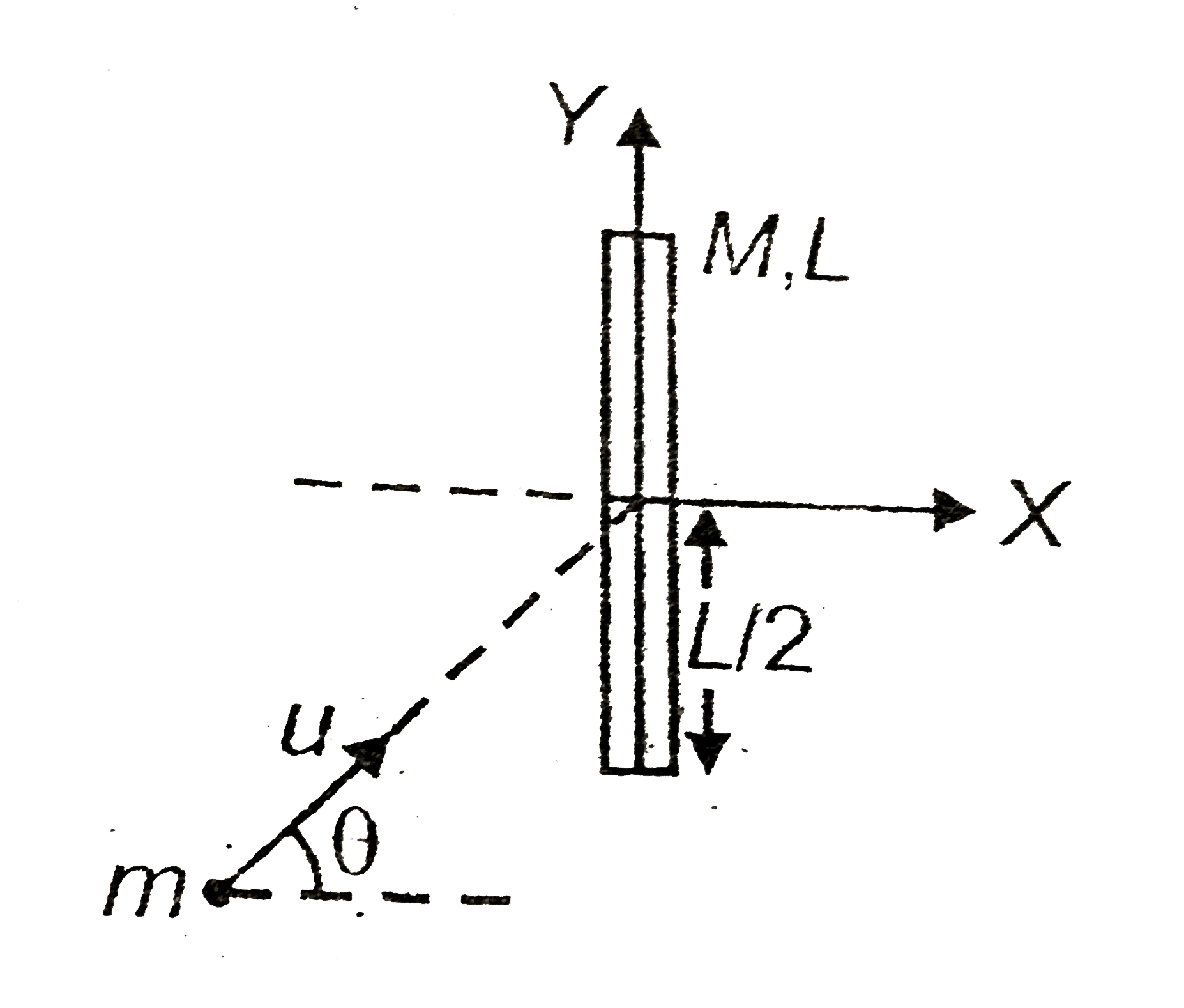
View SolutionA particle of mass m moving in the x direction with speed 2v is hit by another particle of mass 2m moving in they y direction with speed v. If the collision is perfectly inelastic, the percentage loss in the energy during the collision is close to :
View Solution
