Two particles mass m1 and m2 are kept at rest at t=0. They start attracting each other due to their gravitational pull, then
STATEMENT-1 : The toal mometum of the system is zero at any instant.
and
STATEMENT-2 : Both are particles gain equal momentum in opposite direction in equl interval of time as both are acted upon equal and opposite forces.
Statement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-1
Statement -1 is True, Statement-2 is True, Statement is NOT a correct explanation for Statement-1
Statement-1 is True, Statement-2 is False
Statement-1 is False, Statement-2 is True
Step by step video & image solution for Two particles mass m_(1) and m_(2) are kept at rest at t=0. They start attracting each other due to their gravitational pull, then STATEMENT-1 : The toal mometum of the system is zero at any instant. and STATEMENT-2 : Both are particles gain equal momentum in opposite direction in equl interval of time as both are acted upon equal and opposite forces. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTECHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - F) Matrix-Match Type Questions
8 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTECHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - G) Integar Type Questions
9 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTECHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - D) Linked Comprehension Type Questions
20 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - AAKASH INSTITUTECHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))
5 Videos
- TEST 1BOOK - AAKASH INSTITUTECHAPTER - TEST 1EXERCISE - EXERCISE
9 Videos
Similar Questions
Two particles m1 and m2 are initially at rest at infinite distance. Find their relative velocity of approach due to gravitational attraction when their separation is d.
View Solution10 Two particles of masses m1 and m2 initially at rest start moving towards each other under their mutual force of attraction. The speed of the centre of mass at any time t, when they are at a distance r apart, is
View Solution
Knowledge Check
Two particles of mass m1 and m2, approach each other due to their mutual gravitational attraction only. Then
Aacceleration of both the particles are equal.Bacceleration of the particle of mass m1 is proportional to m1Cacceleration the particle of mass m1 is proportional to m2.Daccelaration of the particle of mass m1 is inversely proportional to m1.Two particles of mass m1 and m2, approach each other due to their mutual gravitational attraction only. Then
Aaccelerations of both the particles are equal.Bacceleration of the particle of mass m1 is proportional to m1.Cacceleration of the particle of mass m1 is proportional to m2.Dacceleration of the particle of mass m1 is inversely proportional to m1.Two particles of mass m1 and m2 are approaching towards each other under their mutual gravitational field. If the speed of the particle is v, the speed of the center of mass of the system is equal to :
Am1m2vBZeroC(m1−m2)vm1+m2Dm2m1v
Two particles A and B of mass 1 kg and 4 kg respectively approach each other due to their mutual gravitational force only. Then the ratio of acceleration of A to B at any instant is
View SolutionTwo bodies of masses m1 and m2 are initially at infinite distance at rest. Let they start moving towards each other due to gravitational attraction. Calculate the (i) ratio of accelerations and (ii) speeds at the point where separation between them becomes r.
View SolutionConsider a system of two particles of masses m1 and m2 separated by a distance r. Suppose they start to move towards each other due to their mutual attraction (attractive force may be electrical, gravitational, etc.).
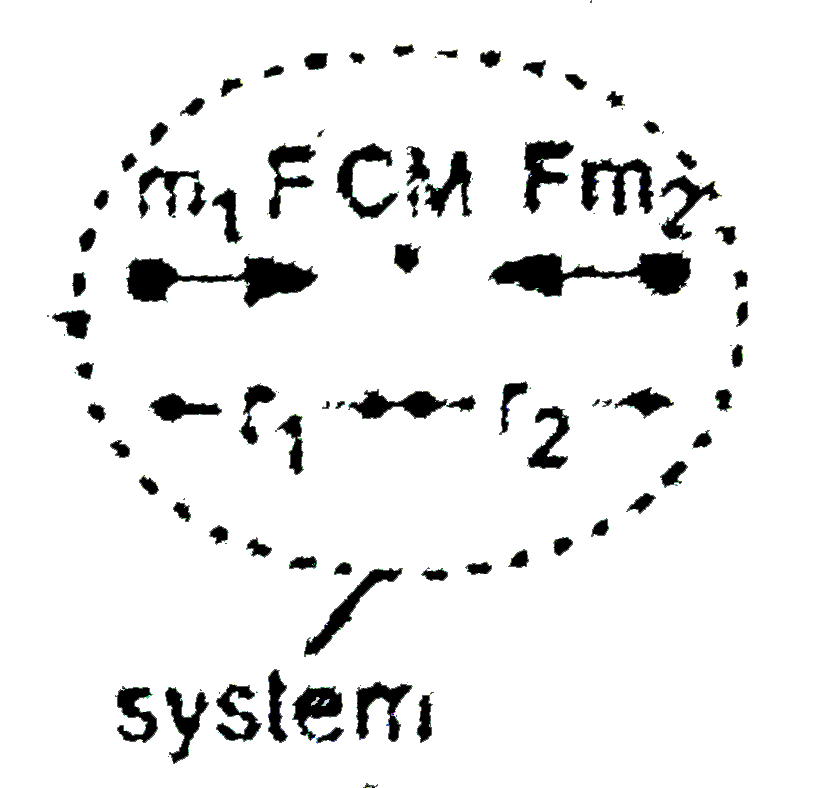
View SolutionIn free space, two particles of mass m each are initially both at rest at a distance a from each other. They start moving towards each other due to their mutual gravitational attraction. The time after which the distance between them has reduced to a2 is:
View SolutionTwo particles of different masses initially at rest, start moving towards each other under their mutual gravitational attraction. At an instant when the speeds of the particles are v and 2v, the speed of the
View Solution
