A semicircle disc of mass M and radius R is held on a rough horizontal surface as shown in figure. The centre of mass C of the disc is at a distance of 4R3π from the point O. Now the disc is released from this position so that it starts rolling without slipping. Find
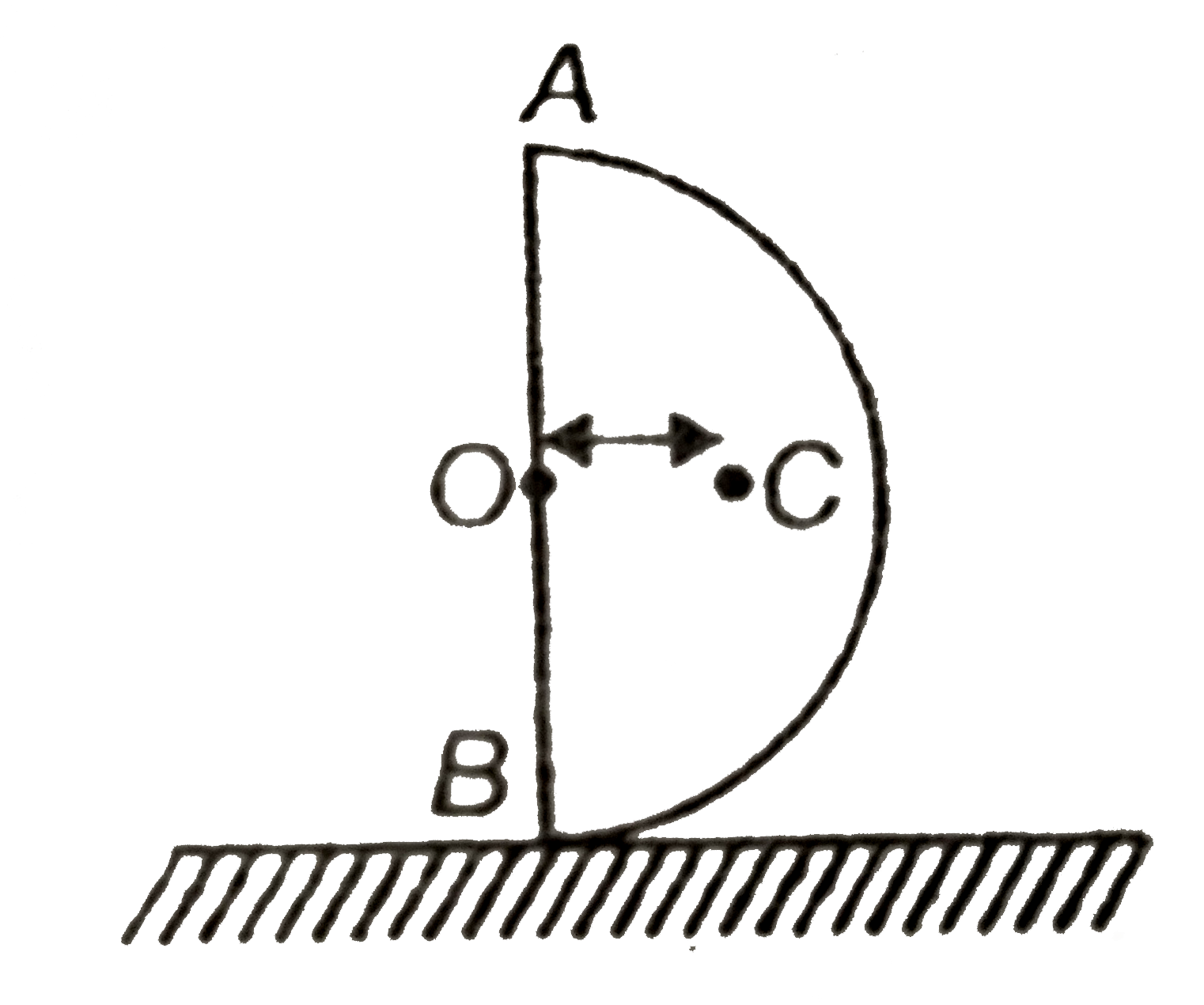
(a) The angular acceleration of the disc at the moment it is relased from the given position.
(b) The minimum co-efficient of fricition between the disc and ground so that it can roll without slipping.
(a)8g9πR (b)24π27π2−32
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - J) Aakash Challengers Questions13videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH INSTITUTECHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Try Yourself63videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH INSTITUTECHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - H) Multiple True-False Type Questions4videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH INSTITUTECHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))5videos
SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITS
- BOOK - AAKASH INSTITUTECHAPTER - TEST 1EXERCISE - EXERCISE9videos
TEST 1
Similar Questions
A disc of mass M and radius R moves in the x-y plane as shown in the figure. The angular momentum of the disc at the instant shown is –
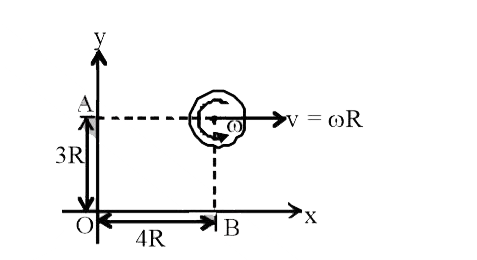 View Solution
View SolutionA disc of mass M and radius R is rolling with angular speed w on horizontal plane as shown. The magnitude of angular momentum of the disc about the origin O is :
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A disc of radius R rolls on a rough horizontal surface. The distance covered by the point A in one revolution is
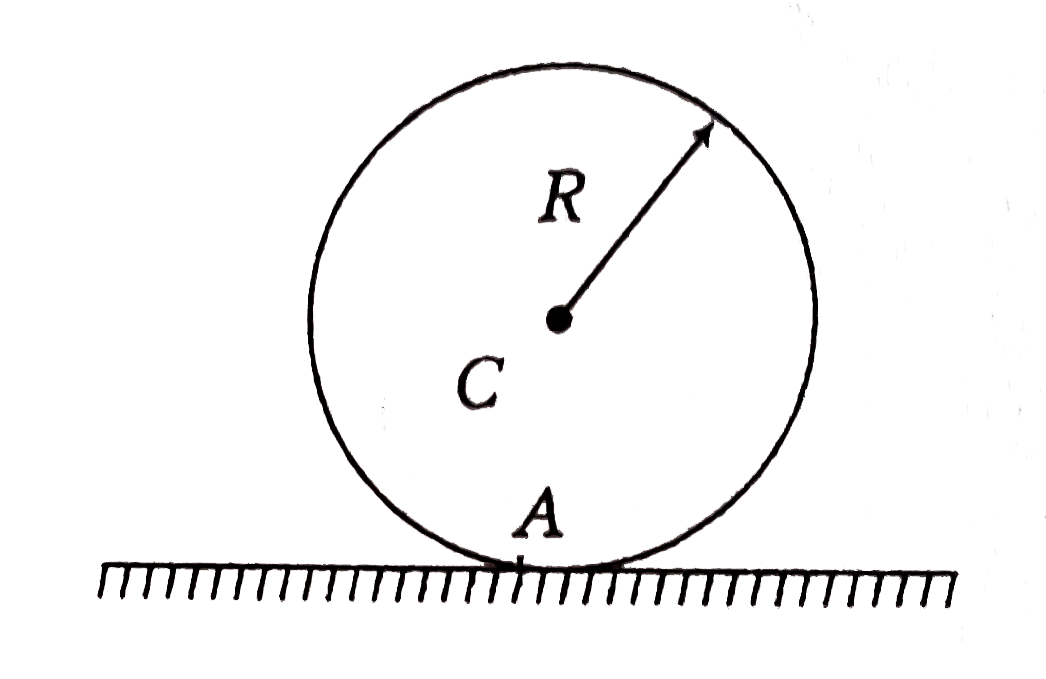 A2πRB2RC8RDπR
A2πRB2RC8RDπR - Question 2 - Select One
A disc of mass m and radius r placed on a routh horizontal surface. A cue of mass m hits the disc at a height h from the axis passing through centre and parallel to the surface. The disc will start pure rolling for.
Ah<r3Bh=r2Ch>r2Dh≥r2 - Question 3 - Select One
A disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be:
 A3v22gB3v24gCv24gDv22g
A3v22gB3v24gCv24gDv22g
A disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be:
 View Solution
View SolutionA disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be :-
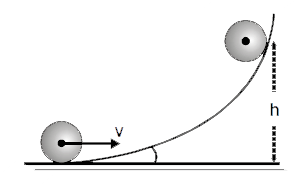 View Solution
View SolutionA thin disc of mass 9M and radius R is given.Now a disc of radius (R/3) is cut as shown in figure.The new position of C .m from orgin will be :-
View SolutionA disc of mass M and radius R is rolling with angular speed ω on a horizontal plane. The magnitude of angular momentum of the disc about a point on ground along the line of motion of disc is :
View SolutionA disc of mass M and radius R can rotate freely in a vertical plane about a horizontal axis at O distance r from the centre of the disc as shown in Fig. The disc is released from rest in the shown position. Answer the following questions based on the above information
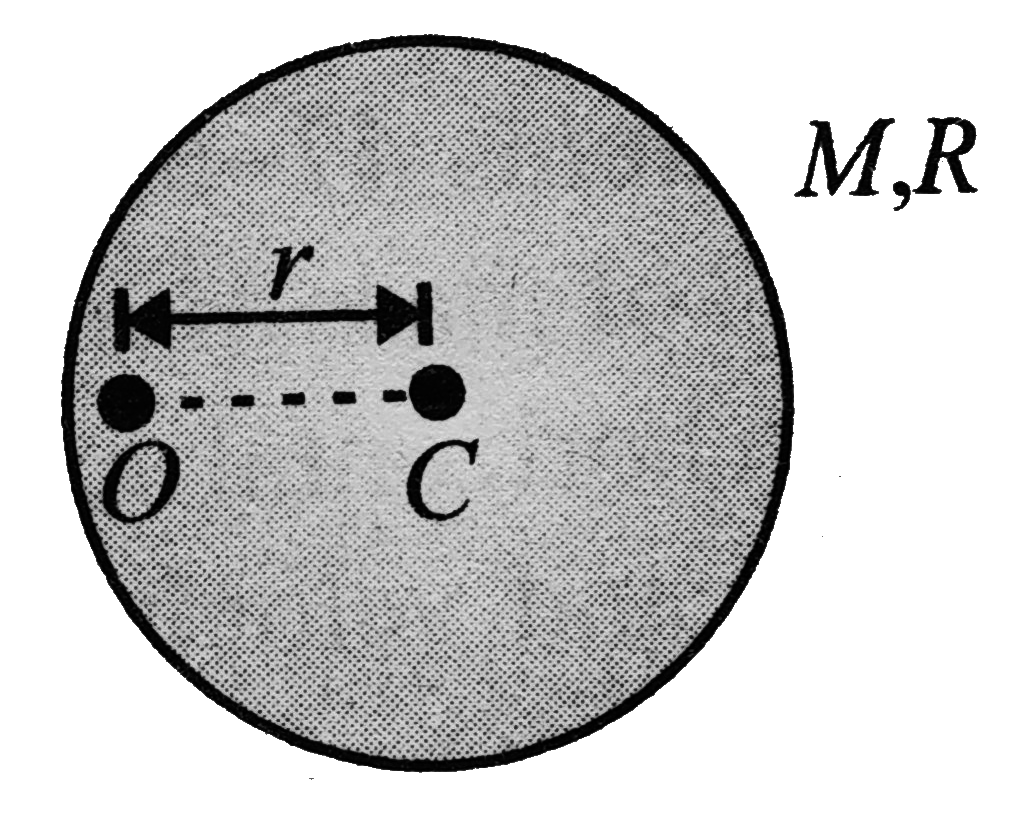
The angular velocity of the disc in the above described case isView Solution

