A thin disc of mass 9M and radius R is given.Now a disc of radius (R/3) is cut as shown in figure.The new position of C .m from orgin will be :-
Step by step video & image solution for A thin disc of mass 9M and radius R is given.Now a disc of radius (R/3) is cut as shown in figure.The new position of C .m from orgin will be :- by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Similar Questions
The figure shows a disc of radius 3R from which a circular hole of radius R is cut as shown in the figure. The distance of the centre of mass of the remaining object from the point O is
 View Solution
View SolutionA circular of radius R has mass 9m . A hole of radius R3 is cut from it as shown in figure. The moment of inertia of the remaining part about an axis passing through centre 0 of the disc and perpendicular of the plane of disc is xmR2 .Find value of x
View Solution
Knowledge Check
- Question 1 - Select One
A thin disc of mass 9M and radius R from which a disc of radius R/3 is cut shown in figure. Then moment of inertia of the remaining disc about O, perpendicular to the plane of disc is -
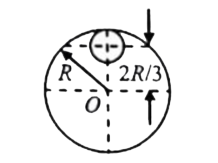 A4MR2B9MR2C379MR2D409MR2
A4MR2B9MR2C379MR2D409MR2 - Question 2 - Select One
A uniform disc of mass M and radius R is liffted using a string as shown in the figure. Then choose incorrect option(s),
 Aits linear acceleration is g upwardBits linear acceleration is g downwardCits angular acceleration is 2gR .Dits rate of change of angular momentum is MgR .
Aits linear acceleration is g upwardBits linear acceleration is g downwardCits angular acceleration is 2gR .Dits rate of change of angular momentum is MgR . - Question 3 - Select One
From a circular disc of radius R and mass 9M, a small disc of radius R/3 is removed as shown in figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is
 A4MR2B409MR2C40MR2D379MR2
A4MR2B409MR2C40MR2D379MR2
A uniform disc of radius R has a round disc of radius R/3 cut as shown in Fig. The mass of the remaining (shaded) portion of the disc equals M. Find the moment of inertia of such a disc relative to the axis passing through geometrical centre of original disc and perpendicular to the plane of the disc.
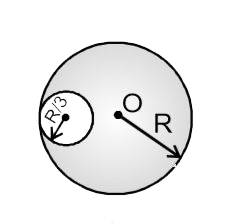 View Solution
View SolutionA semicircle disc of mass M and radius R is held on a rough horizontal surface as shown in figure. The centre of mass C of the disc is at a distance of 4R3π from the point O. Now the disc is released from this position so that it starts rolling without slipping. Find
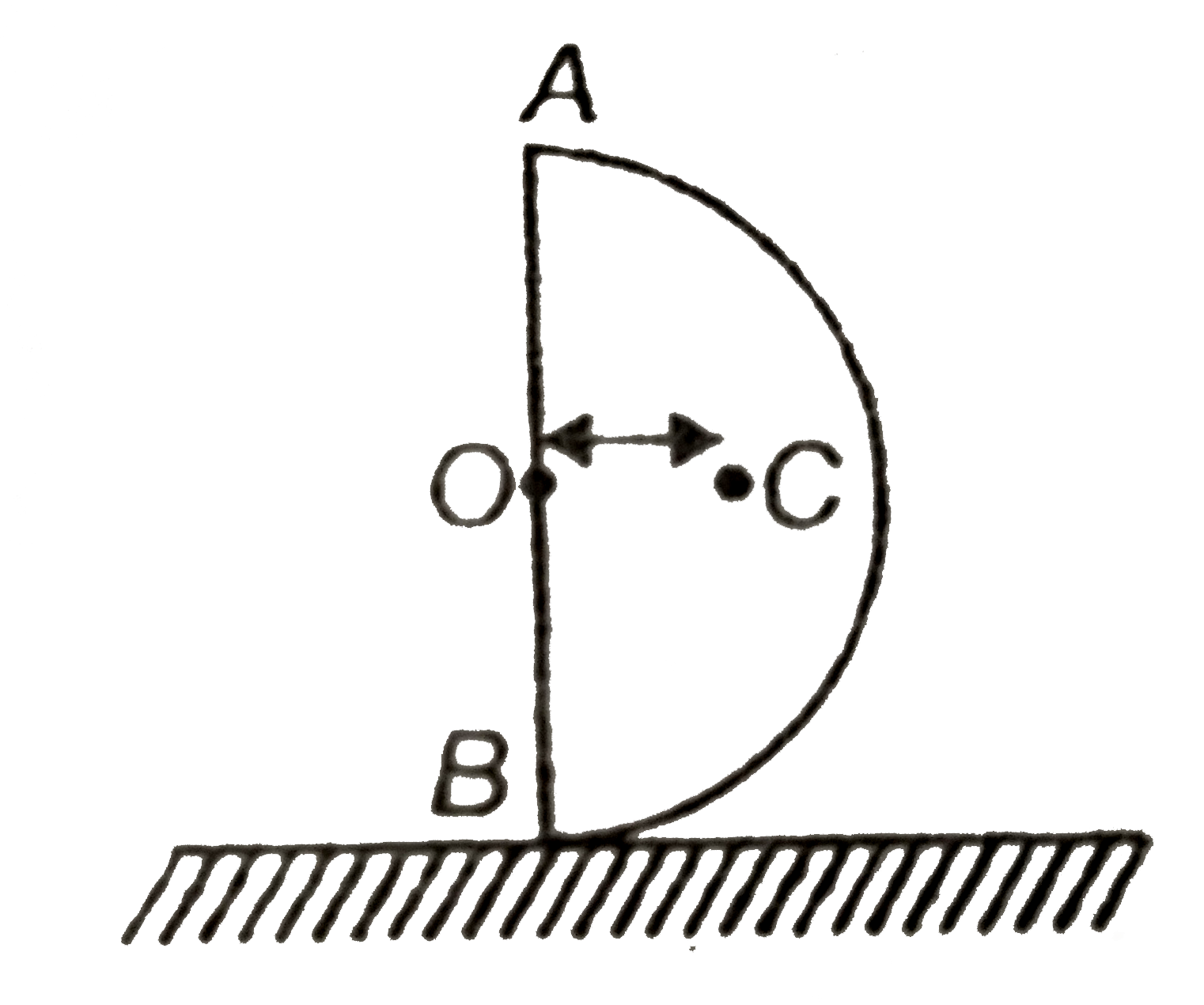
(a) The angular acceleration of the disc at the moment it is relased from the given position.
(b) The minimum co-efficient of fricition between the disc and ground so that it can roll without slipping.View SolutionFrom a uniform disc of radius R, an equilateral triangle of side √3R is cut as shown in the figure. The new position of centre of mass is :
 View Solution
View SolutionA uniform disc of mass m & radius R is pivoted at its centre O with its plane vertical as shown in figure A circular portion of disc of radius R2 is removed from it. Then choose the correct option(s)
 View Solution
View SolutionTwo thin discs each of mass M and radius r metre are attached to form a rigid body as shown in figure. The rotational inertia of this body about an axis perpendicular to the plane of disc B and passing through its centre is
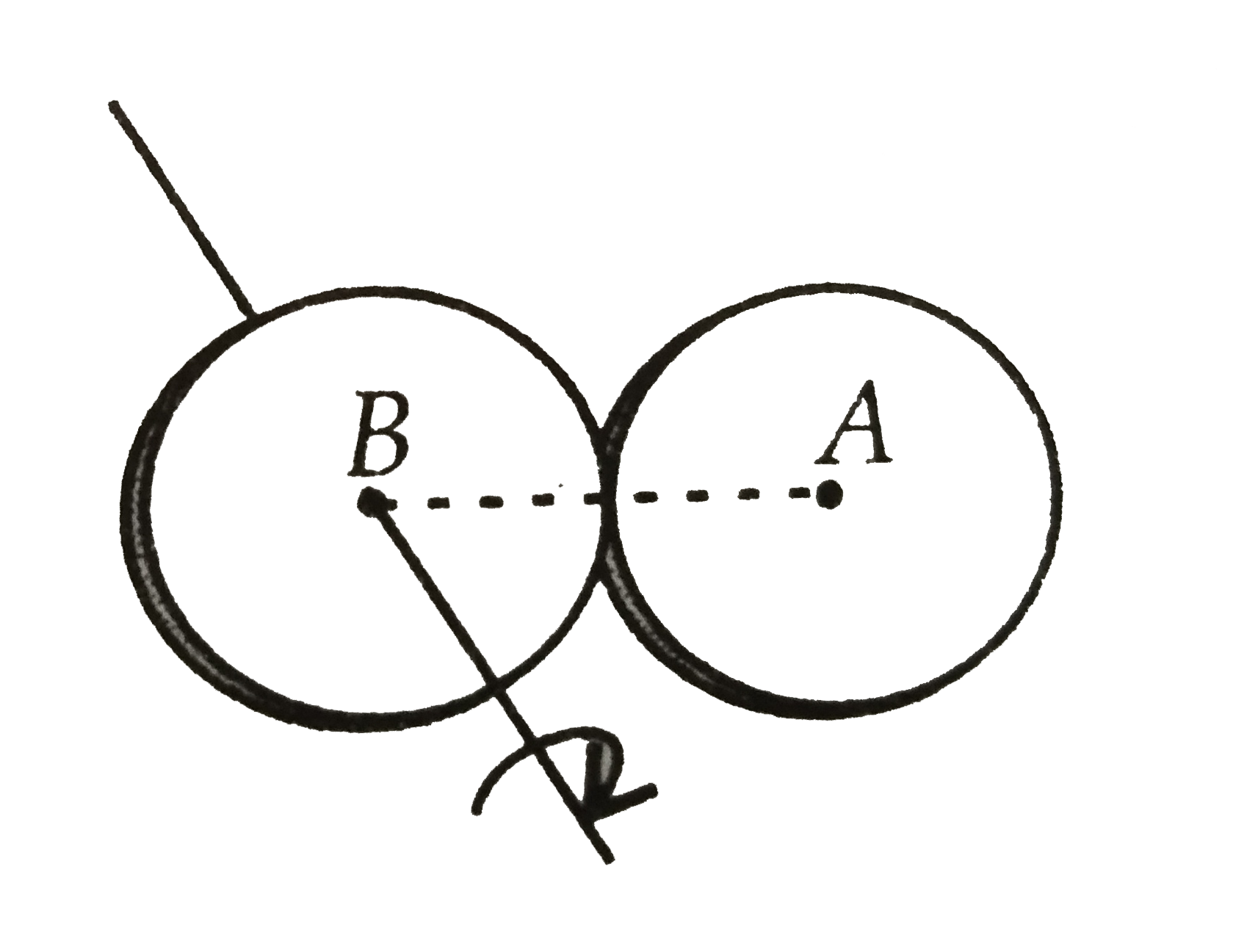 View Solution
View Solution
