A particle is projected vertically upward with with velocity √23GMR from the surface of Earth. The height attained by it is (G, M, R have usual meanings)
3R
R2
2R
R3
The correct Answer is:B
To solve the problem of finding the height attained by a particle projected vertically upward with a given initial velocity from the surface of the Earth, we can use the principle of conservation of energy.
Given:
- Initial velocity v0=√23GMR
- G = gravitational constant
- M = mass of the Earth
- R = radius of the Earth
Step 1: Calculate the initial kinetic energy (KE) at the surface
The initial kinetic energy of the particle when it is projected is given by:
KE=12mv20
Substituting the value of v0:
KE=12m(√23GMR)2=12m⋅23⋅GMR=mGM3R
Step 2: Calculate the gravitational potential energy (PE) at the surface
The gravitational potential energy at the surface of the Earth is given by:
PE=−GMmR
Step 3: Calculate the total mechanical energy (E) at the surface
The total mechanical energy at the surface is the sum of kinetic and potential energy:
E=KE+PE=mGM3R−GMmR
Combining the terms:
E=mGM3R−3mGM3R=−2mGM3R
Step 4: Calculate the total mechanical energy at height h
At the height h, the potential energy becomes:
PEh=−GMmR+h
The kinetic energy at the maximum height is zero (as the particle comes to rest at the highest point). Thus, the total mechanical energy at height h is:
Eh=0−GMmR+h=−GMmR+h
Step 5: Set the total mechanical energy at the surface equal to that at height h
Using conservation of energy:
−2mGM3R=−GMmR+h
Cancelling −GMm from both sides:
23R=1R+h
Step 6: Solve for h
Cross-multiplying gives:
2(R+h)=3R
Expanding and rearranging:
2R+2h=3R⟹2h=3R−2R⟹2h=R⟹h=R2
Final Answer:
The height attained by the particle is:
h=R2
---
- Initial velocity v0=√23GMR
- G = gravitational constant
- M = mass of the Earth
- R = radius of the Earth
The initial kinetic energy of the particle when it is projected is given by:
KE=12mv20
Substituting the value of v0:
KE=12m(√23GMR)2=12m⋅23⋅GMR=mGM3R
The gravitational potential energy at the surface of the Earth is given by:
PE=−GMmR
The total mechanical energy at the surface is the sum of kinetic and potential energy:
E=KE+PE=mGM3R−GMmR
Combining the terms:
E=mGM3R−3mGM3R=−2mGM3R
At the height h, the potential energy becomes:
PEh=−GMmR+h
The kinetic energy at the maximum height is zero (as the particle comes to rest at the highest point). Thus, the total mechanical energy at height h is:
Eh=0−GMmR+h=−GMmR+h
Using conservation of energy:
−2mGM3R=−GMmR+h
Cancelling −GMm from both sides:
23R=1R+h
Cross-multiplying gives:
2(R+h)=3R
Expanding and rearranging:
2R+2h=3R⟹2h=3R−2R⟹2h=R⟹h=R2
The height attained by the particle is:
h=R2
Topper's Solved these Questions
- GRAVITATION BOOK - AAKASH INSTITUTECHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION -C (Objective Type Questions (More than one option are correct))
11 Videos
- GRAVITATION BOOK - AAKASH INSTITUTECHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION -D (Linked Comprehension Type Questions)
13 Videos
- GRAVITATION BOOK - AAKASH INSTITUTECHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION -A (Objective Type Questions (one option is correct))
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTECHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - D
13 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTECHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
Similar Questions
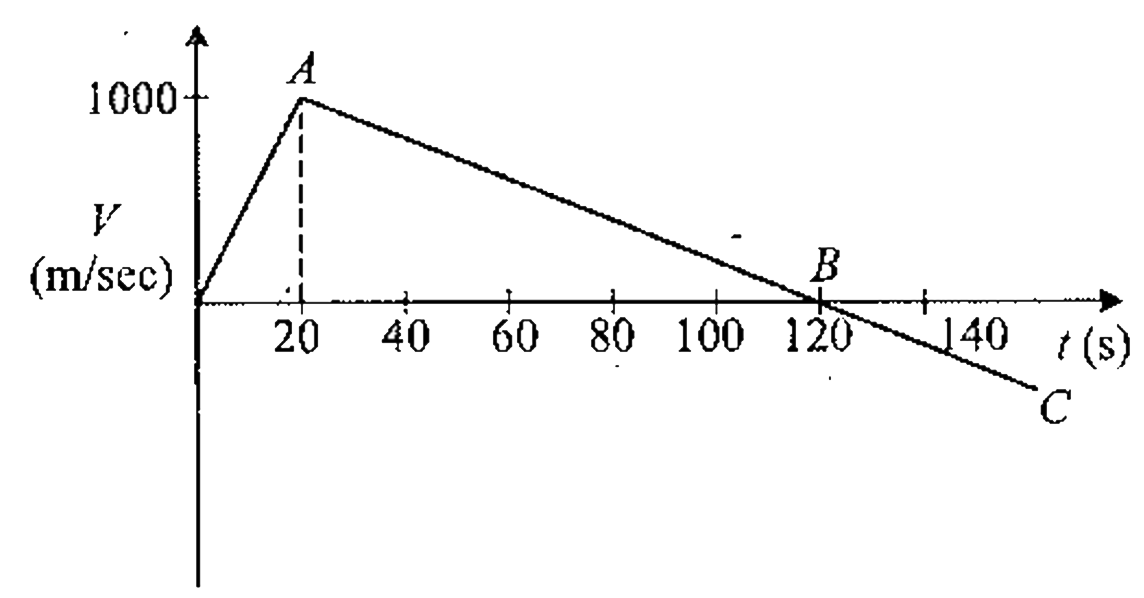
A rocket is projected vertically upwards and its time velocity graph is shown in the figure-1.115. The maximum height attained by the rocket is :
View SolutionThree particles are projected vertically upward from a point on the surface of the earth with velocities √2gR/3 surface of the earth. The maximum heights attained are respectively h1,h2,h3.
View Solution
Knowledge Check
A particle is projected vertically upwards with a velocity √gR, where R denotes the radius of the earth and g the acceleration due to gravity on the surface of the earth. Then the maximum height ascended by the particle is
AReB2ReCRe2DNone of theseA body is projected vertically upwards with a speed of √GMR ( M is mass and R is radius of earth ) . The body will attain a height of
AR2BRC54RD3R2A particle is projected vertically with speed V from the surface of the earth . Maximum height attained by the particle , in term of the radius of earth R,V and g is ( V < escape velocity , g is the acceleration due to gravity on the surface of the earth )
A3RV22gR−2V2B2RV23gR−V2CRV22gR−V2DRV2gR−2V2
A tunnel is dug inside the earth across one of its diameters. Radius of earth is R and its mass is M. A particle is projected inside the tunnel with velocity √2GMR from one of its ends then maximum velocity attained by the particle in the subsequent motion is (assuming tunnel to be frictionless)
View SolutionA particle is projected vertically up with velocity v=√4gRe3 from earth surface.The velocity of particle at height equal to half of the maximum height reached by it
View SolutionA particle is projected vertically upwards with a velocity √gR, where R denotes the radius of the earth and g the acceleration due to gravity on the surface of the earth. Then the maximum height ascended by the particle is
View SolutionA particle is thrown vertically upwards. If its velocity is half of the maximum height is 20m/s, then maximum height attained by it is
View SolutionIf an object is projected vertically upwards with speed , half the escape speed of earth , then the aximum height attained by it is [ R is radius of earth ]
View Solution