A solid cylinder of height h and mass m floats in a liquid of density ρ such that three fourth of its height is immersed. Now, the cylinder is released inside a liquid of density ρ4, contained in a downward accelerated vessel. Find the magnitude of acceleration of vessel A, for which cylinder sinks with relative acceleration of A3 w.r.t. vessel.
2g3
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTECHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - I
6 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTECHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTECHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment(Section-D)
12 Videos
Similar Questions
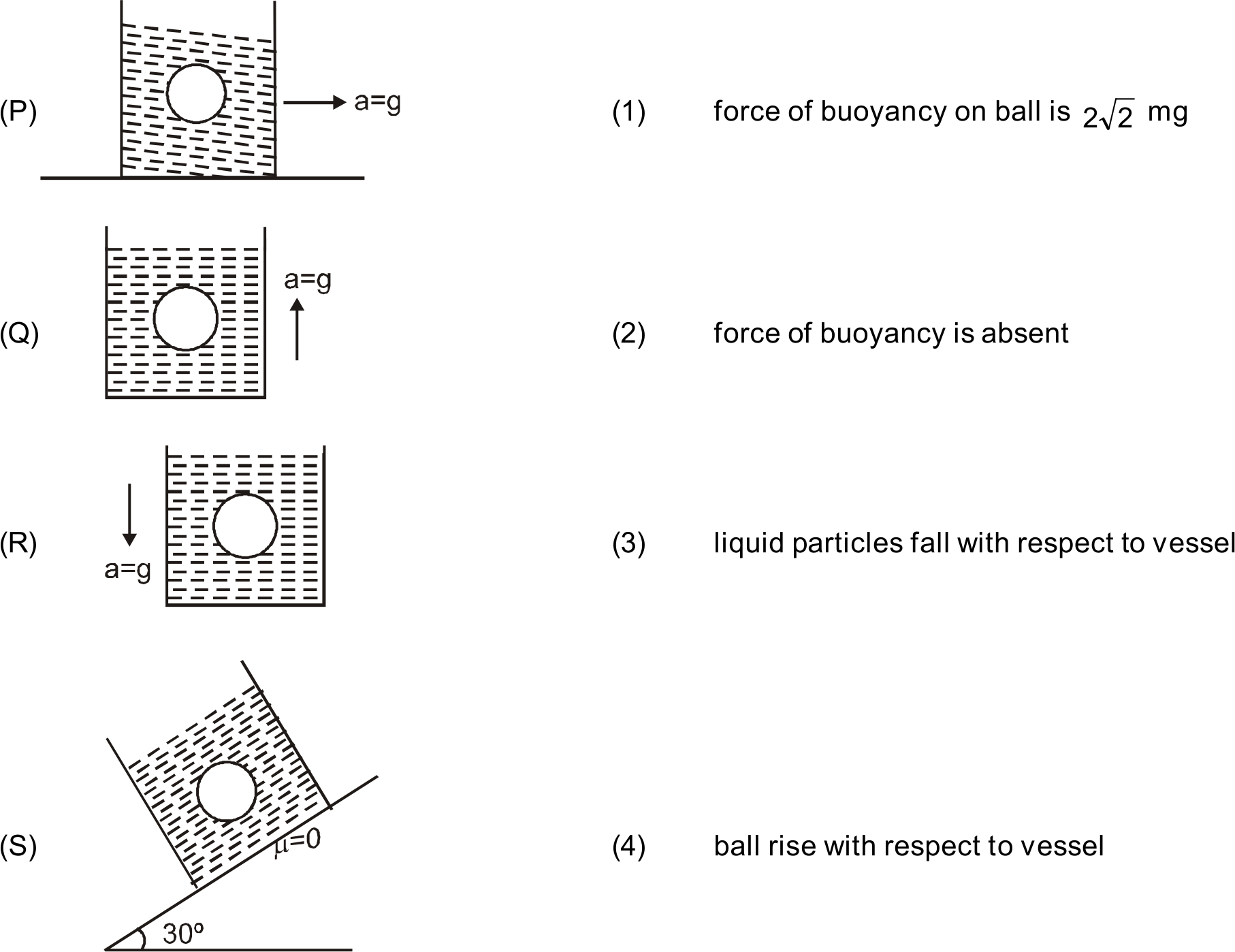
A ball of mass m and density ρ2 is completely immersed in a liquid of density ρ, contained in an accelerating vessel as shown.Select the correct answer using the codes given below the columns.
View SolutionA solid cylinder of height h and mass m is floating in a liquid of density ρ as shown in the figure. Find the acceleration of the vessel (in m/s2) containing liquid for which the relative downward acceleration of the completely immersed cylinder w.r.t. vessel becomes equal to one-third of that of the vessel. (Take g=10m/s2)

View Solution
Knowledge Check
A cylinder of mass m and density ρ hanging from a string is lowered into a vessel of cross-section area s containing a liquid of density σ(<ρ) unit it is fully immersed. The increase in pressure at the bottom of the vessel is
AmρgσsBmgsCmσgρsDzeroA uniform cube of mass M is floating on the surface of a liquid with three fourth of its volume immersed in the liquid (density=ρ). The length of the side of the cube is equal to
 A(4M/3ρ)2/3B(M/3ρ)2/3C(M/4ρ)2/3DNone of these
A(4M/3ρ)2/3B(M/3ρ)2/3C(M/4ρ)2/3DNone of these
A solid cylinder of height h and mass m is floating in a liquid of density ρ as shown in the figure. Find the acceleration of the vessel (in m/s2) containing liquid for which the relative downward acceleration of the completely immersed cylinder w.r.t. vessel becomes equal to one-third of that of the vessel. (Take g = 10 m//s^(2))
View SolutionA solid cylinder of height h and mass m is floating in a liquid of density ρ as shown in the figure. Find the acceleration of the vessel (in m/s2) containing liquid for which the relative downward acceleration of the completely immersed cylinder w.r.t. vessel becomes equal to one-third of that of the vessel. (Take g=10m/s2)

View SolutionA container having a liquid of density ρ is moving downwards with acceleration g2. Find the pressure difference between two vertical points in the liquid separated by h
View SolutionA ball of density ais released from rest from the centre of an accelerating sealed cubical vessel completely filled with a liquid of density ρ. If the trough moves with a horizontal acceleration →a0 find the initial acceleration of the ball.
View SolutionA ball of density ais released from rest from the centre of an accelerating sealed cubical vessel completely filled with a liquid of density ρ. If the trough moves with a horizontal acceleration →a0 find the initial acceleration of the ball.
View SolutionA uniform cube of mass M is floating on the surface of a liquid with three fourth of its volume immersed in the liquid (density=ρ). The length of the side of the cube is equal to

View Solution
