A ball of density ais released from rest from the centre of an accelerating sealed cubical vessel completely filled with a liquid of density ρ. If the trough moves with a horizontal acceleration →a0 find the initial acceleration of the ball.
The correct Answer is:gˆj
To solve the problem of finding the initial acceleration of a ball of density σ released from rest in an accelerating sealed cubical vessel filled with a liquid of density ρ, we can follow these steps:
Step 1: Understand the Forces Acting on the Ball
When the ball is released, it experiences two main forces:
1. The gravitational force acting downwards, which is Fg=mg=Vσg, where V is the volume of the ball.
2. The buoyant force acting upwards due to the liquid, which is Fb=Vρg.
Step 2: Set Up the Free Body Diagram
We can analyze the forces in both the horizontal and vertical directions. The vessel is accelerating horizontally with an acceleration →a0.
Step 3: Analyze the Horizontal Motion
In the horizontal direction, the ball will experience an effective acceleration due to the acceleration of the vessel. The net horizontal force on the ball can be expressed as:
Fx=max=Vρa0
where ax is the horizontal acceleration of the ball.
Step 4: Analyze the Vertical Motion
In the vertical direction, the net force acting on the ball is:
Fy=Fb−Fg=Vρg−Vσg
This can be simplified to:
Fy=V(ρ−σ)g
Step 5: Apply Newton's Second Law
Using Newton's second law in both directions, we can write:
1. For horizontal motion:
max=Vρa0
Thus,
ax=Vρa0m
Since m=Vσ, we have:
ax=ρa0σ
2. For vertical motion:
may=V(ρ−σ)g
Thus,
ay=V(ρ−σ)gm
Again substituting m=Vσ:
ay=(ρ−σ)gσ
Step 6: Combine the Accelerations
The net acceleration →a of the ball can be expressed as a vector sum of the horizontal and vertical components:
→a=ax^i+ay^j
Substituting the values we found:
→a=(ρa0σ)^i+((ρ−σ)gσ)^j
Final Result
Thus, the initial acceleration of the ball is given by:
→a=(ρa0σ)^i+((ρ−σ)gσ)^j
When the ball is released, it experiences two main forces:
1. The gravitational force acting downwards, which is Fg=mg=Vσg, where V is the volume of the ball.
2. The buoyant force acting upwards due to the liquid, which is Fb=Vρg.
We can analyze the forces in both the horizontal and vertical directions. The vessel is accelerating horizontally with an acceleration →a0.
In the horizontal direction, the ball will experience an effective acceleration due to the acceleration of the vessel. The net horizontal force on the ball can be expressed as:
Fx=max=Vρa0
where ax is the horizontal acceleration of the ball.
In the vertical direction, the net force acting on the ball is:
Fy=Fb−Fg=Vρg−Vσg
This can be simplified to:
Fy=V(ρ−σ)g
Using Newton's second law in both directions, we can write:
1. For horizontal motion:
max=Vρa0
Thus,
ax=Vρa0m
Since m=Vσ, we have:
ax=ρa0σ
may=V(ρ−σ)g
Thus,
ay=V(ρ−σ)gm
Again substituting m=Vσ:
ay=(ρ−σ)gσ
The net acceleration →a of the ball can be expressed as a vector sum of the horizontal and vertical components:
→a=ax^i+ay^j
Substituting the values we found:
→a=(ρa0σ)^i+((ρ−σ)gσ)^j
Thus, the initial acceleration of the ball is given by:
→a=(ρa0σ)^i+((ρ−σ)gσ)^j
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Single Correct
95 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Multipe Correct
15 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.4
10 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions

A sealed tank containing a liquid of density ρ moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B is
View SolutionA ball of density ρ is released from deep inside of a liquid of density 2ρ. It will move up
View SolutionA small solid ball of density ρ is held inside at point A of a cubical container of side L, filled with an ideal liquid of density 4ρ as shown in the figure. Now, if the container starts moving with constant acceleration a horizontally and the ball is released from point A simultaneously, then choose from following the correct option(s)

View SolutionA rectangular box is completely filled with a liquid of density ρ, as shown in Fig. The box is accelerated horizontally with a constant acceleration a. Determine the gauge pressures at the four points A,B,C and D.
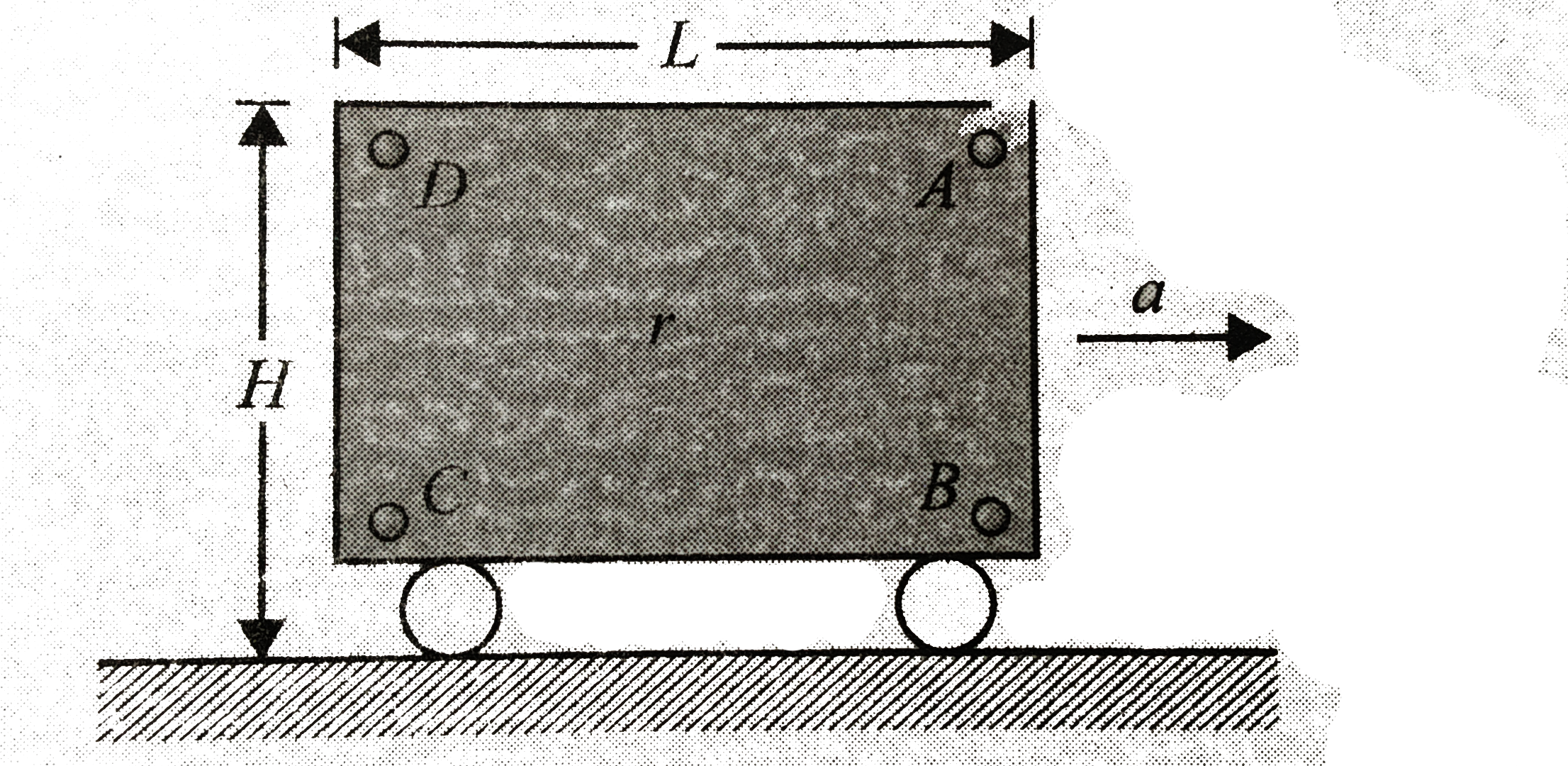
View SolutionA sealed tank containing a liquid of density ρ moves with horizontal acceleration a as shown in the figure. The difference in pressure between two points A and B will be

View SolutionA cubical vessel (open from top) of side L is filled with a liquid of density ρ.
What is the torque of hydrostatic force on a side wall about an axis passing through one of the bottom edges?
View SolutionA cubical vessel (open from top) of side L is filled with a liquid of density ρ.
What is the ratio of magnitude of torque on one side wall to the torque on base about the same axis
View SolutionA beaker containing a liquid of density ρ moves up with an acceleration a. The pressure due to the liquid at a depth h below the free surface of the liquid is.
View Solutionwhen a proton is released from rest in a room, it starts with an initial acceleration a0 towards west . When it is projected towards north with a speed v0, it moves with an initial acceleration 3a0 towards west. Find the elecrtic field and the minimum possible magnetic field in the room.
View SolutionWhen a proton is released from rest in a room, it starts with an initial acceleration a0 towards west. When it is projected towards north with a speed v0 it moves with an initial acceleration 3a0 towards west. The electric and magnetic fields in the room are
View Solution
