A spring of force constant 600Nm−1 is mounted on a horizontal table. A mass of 1.5 kg is attached to the free end of the spring, pulled sideways to a distance of 2 cm and released .P.E. of the mass when it momentarily comes to rest and total energy are
0.12J,0
0,0.12J
0,0
0.12J,0.12J
The correct Answer is:4
To solve the problem, we need to calculate the potential energy (P.E.) of the mass when it momentarily comes to rest and the total energy of the spring-mass system.
1. Identify Given Values:
- Force constant of the spring, k=600N/m
- Mass attached to the spring, m=1.5kg
- Displacement from the equilibrium position (amplitude), x=2cm=0.02m
2. Understand the Energy in the System:
- When the mass is pulled to the maximum displacement (2 cm) and released, it will momentarily come to rest at that point. At this point, all the energy in the system is potential energy (P.E.), and the kinetic energy (K.E.) is zero.
3. Calculate the Potential Energy:
- The formula for potential energy stored in a spring is given by:
P.E.=12kx2
- Substituting the values:
P.E.=12×600N/m×(0.02m)2
P.E.=12×600×0.0004
P.E.=0.12J
4. Calculate the Total Energy:
- The total mechanical energy in the spring-mass system is equal to the potential energy at maximum displacement since all the energy is stored as potential energy at that point.
- Therefore, the total energy E is:
E=P.E.=0.12J
5. Final Answers:
- Potential Energy when the mass comes to rest: 0.12J
- Total Energy of the system: 0.12J
Summary:
- The potential energy of the mass when it momentarily comes to rest is 0.12J.
- The total energy of the system is also 0.12J.
- Force constant of the spring, k=600N/m
- Mass attached to the spring, m=1.5kg
- Displacement from the equilibrium position (amplitude), x=2cm=0.02m
- When the mass is pulled to the maximum displacement (2 cm) and released, it will momentarily come to rest at that point. At this point, all the energy in the system is potential energy (P.E.), and the kinetic energy (K.E.) is zero.
- The formula for potential energy stored in a spring is given by:
P.E.=12kx2
- Substituting the values:
P.E.=12×600N/m×(0.02m)2
P.E.=12×600×0.0004
P.E.=0.12J
- The total mechanical energy in the spring-mass system is equal to the potential energy at maximum displacement since all the energy is stored as potential energy at that point.
- Therefore, the total energy E is:
E=P.E.=0.12J
- Potential Energy when the mass comes to rest: 0.12J
- Total Energy of the system: 0.12J
- The potential energy of the mass when it momentarily comes to rest is 0.12J.
- The total energy of the system is also 0.12J.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT (SECTION-B )25videos
OSCILLATIONS
- BOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT ( SECTION-C )11videos
OSCILLATIONS
- BOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - Try Yourself86videos
OSCILLATIONS
- BOOK - AAKASH INSTITUTECHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)10videos
NUCLEI
- BOOK - AAKASH INSTITUTECHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)5videos
PHYSICAL WORLD
Similar Questions
A spring of force constant 1200Nm−1 is mounted on a horizontal table as shown in figure. A mass of 3.0kg is attached to the free end of the spring, pulled side ways to a distance of 2.0cm and released , what is
(a) the speed of the mass when the spring is compressed by 1.0cm?
Potential energy of the mass when it momentarily comed to rest ?
(c) Total energy of the oscillating mass.
 View Solution
View SolutionA spring of force constant 1200Nm−1 is mounted on a horizontal table as shown in figure. A mass of 3.0kg is attached to the free end of the spring, pulled side ways to a distance of 2.0cm and released. Determing.
(a) the frequency of oscillation of the mass.
(b) the maximum acceleration of the mass.
(c) the maximum speed of the mass.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A spring of force constant 600Nm−1 is mounted on a horizontal table. A mass of 1.5 kg is attached to the free end of the spring,pulled sideways to a distance of 2 cm and released . The speed of the mass when the spring is compressed by 1 cm is
A0.175ms−1B0.35ms−1C0.7ms−1D1.4ms−1 - Question 2 - Select One
A weightless spring of length 60 cm and force constant 100Nm−1 is kept straight and unstretched on a smooth horizontal table and its ends are rigidly fixed. A mass of 0.25 kg is attached at the middle of the spring and is slightly displaced along the length. The time period of the oscillation of the mass is
Aπ20 sBπ10 sCπ5 sDπ√200 s - Question 3 - Select One
Spring of spring constant 1200Nm−1 is mounted on a smooth fricationless surface and attached to a block of mass 3kg. Block is pulled 2cm to the right and released. The angular frequency of oscillation is
_S01_037_Q01.png) A5rad/secB30rad/secC10rad/secD20rad/sec
A5rad/secB30rad/secC10rad/secD20rad/sec
A mass of 5 kg is attached to the free end of a spring pulled sideways to a distance of 3 cm and released. What will be the

(a) Speed of this mass when spring is compressed by 2 cm ?
(b) Potential energy of the mass at the point where kinetic energy becomes zero ?View SolutionIn the above example, what is (i) the speed of te mass when the spring is compressed by 1.0 cm, (ii) potential energy of the mass when it momentarily comes to rest, (iii) total energy of the oscillating mass.
View SolutionOne end of a spring of force constant k1 is attached to the ceiling of an elevator. A block of mass 1.5kg is attached to the other end. Another spring of force constant k2 is attached to the bottom of the mass and to the floor of the elevator as shown in figure. At equilibrium, the deformation in both the spring is equal and is 40cm. If the elevator moves with constant acceleration upward, the additional deformation in both the spring is 8cm. Find the elevator's accelerationn ( g=10ms−2).
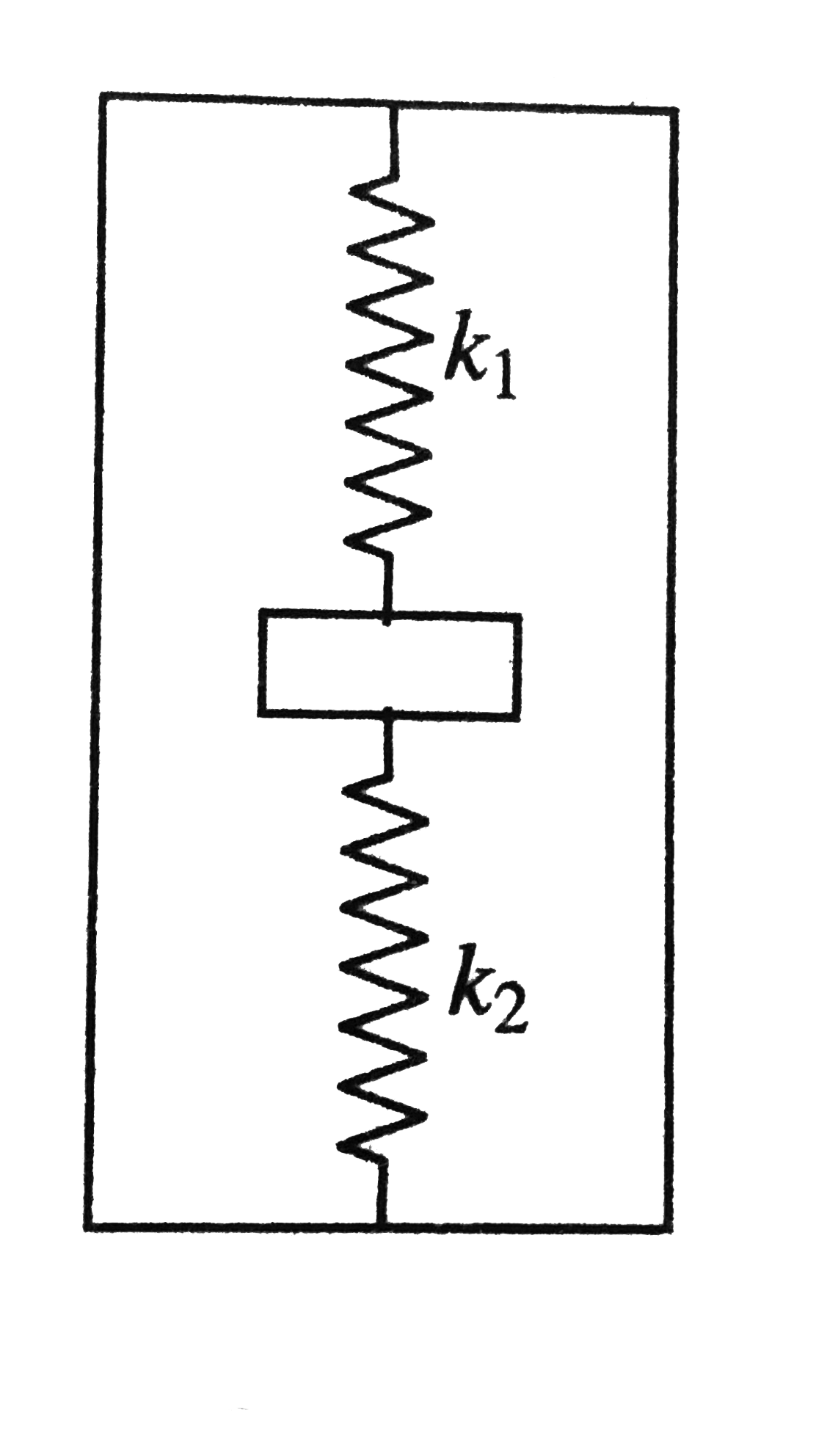 View Solution
View SolutionA weightless spring of length 60 cm and force constant 200 N/m is kept straight and unstretched on a smooth horizontal table and its ends are rigidly fixed. A mass of 0.25 kg is attached at the middle of the spring and is slightly displaced along the length. The time period of the oscillation of the mass is
View SolutionA spring of force constant K rests on a smooth floor, with one end fixed to a wall. A block of mass m hits the free end of the spring with velocity v. The maximum force exerted by the spring on the wall is
View Solution

