A particle of mass 4 kg moves along x axis, potential energy ( U ) varies with respect to x as U=20+(x−4)2 , maximum speed of paritcle is at
x=4
x=2
x=0
x=2.5
The correct Answer is:1
To find the position where the particle of mass 4 kg has its maximum speed, we need to analyze the potential energy function given by:
U(x)=20+(x−4)2
Step 1: Understand the Potential Energy Function
The potential energy function indicates how the potential energy varies with the position x. The term (x−4)2 suggests that the potential energy reaches its minimum when x=4.
Step 2: Find the Minimum Potential Energy
To find the minimum potential energy, we can evaluate the potential energy function at x=4:
U(4)=20+(4−4)2=20+0=20
Step 3: Determine Conditions for Maximum Speed
In mechanics, the total mechanical energy E of a system is conserved and is the sum of kinetic energy K and potential energy U:
E=K+U
The kinetic energy K is given by:
K=12mv2
For maximum speed, the kinetic energy must be maximized, which occurs when the potential energy is minimized. Therefore, the maximum speed will occur when the potential energy is at its minimum value.
Step 4: Identify the Position for Maximum Speed
Since we found that the potential energy is minimized at x=4, this is the position where the particle will have its maximum speed.
Conclusion
Thus, the maximum speed of the particle occurs at:
Maximum speed is at x=4
---
The potential energy function indicates how the potential energy varies with the position x. The term (x−4)2 suggests that the potential energy reaches its minimum when x=4.
To find the minimum potential energy, we can evaluate the potential energy function at x=4:
In mechanics, the total mechanical energy E of a system is conserved and is the sum of kinetic energy K and potential energy U:
Since we found that the potential energy is minimized at x=4, this is the position where the particle will have its maximum speed.
Thus, the maximum speed of the particle occurs at:
Topper's Solved these Questions
- OSCILLATIONSBOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT ( SECTION-C )
11 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT (SECTION -D( Comprehension) )
1 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT ( SECTION -A)
58 Videos
- NUCLEIBOOK - AAKASH INSTITUTECHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
- PHYSICAL WORLDBOOK - AAKASH INSTITUTECHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)
5 Videos
Similar Questions
A single conservative force F(x) acts on a on a (1.0kg ) particle that moves along the x-axis. The potential energy U(x) is given by:
U(x)=20+(x−2)2
where, x is meters. At x=5.0m the particle has a kinetic energy of 20J
(a) What is the mechanical energy of the system?
(b) Make a plot of U(x) as a function of x for −10m≤x≤10m, and on the same graph draw the line that represents the mechanical energy of the system. Use part (b) to determine.
(c) The least value of x and
(d) the greatest value of x between which the particle can move.
(e) The maximum kinetic energy of the particle and
(f) the value of x at which it occurs.
(g) Datermine the equation for F(x) as a function of x.
(h) For what (finite ) value of x does F(x)=0?.
View SolutionA particle of mass = 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is nπ5 second. Find value of n.
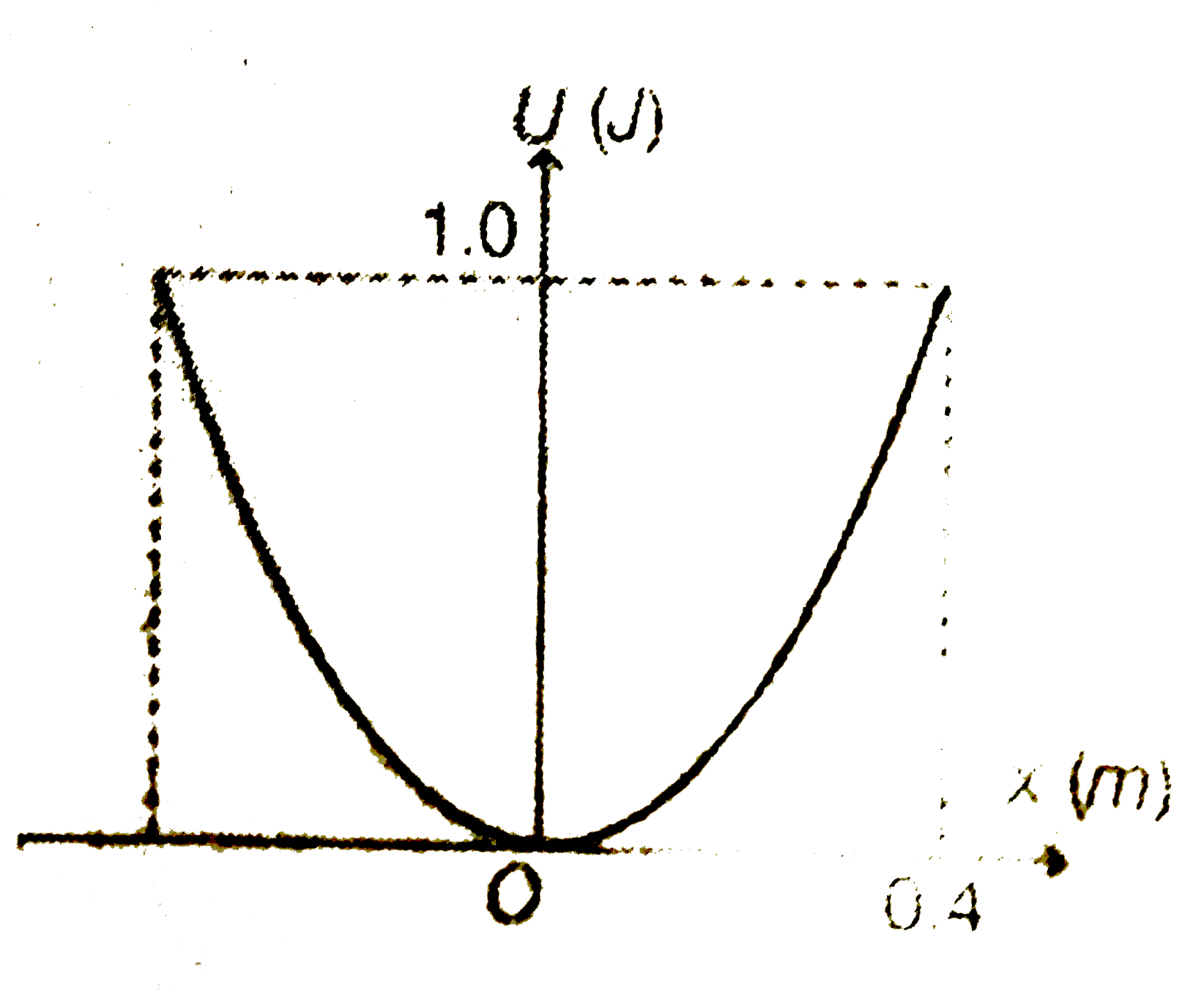
View Solution
Knowledge Check
A particle of mass 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is
 A2π5sB2√2π5sC√2π5sD4π5s
A2π5sB2√2π5sC√2π5sD4π5sA single conservative force F(x) acts on a 1.0−kg particle that moves along the x-axis. The potential energy U(x) is given by U(x)=20+(x−2)2 where x is in meters. At x=5.0m, the particle has a kinetic energy of 20J.
The maximum kinetic energy of the particle and the value of x at which maximum kinetic energy occurs areA(a) 29J,0mB(b) 49J,0mC(c) 49J,2mD(d) 29J,2mThe potential energy of a particle oscillating on x-axis is given as U+20+(x−2)2. The mean position is at
Ax=2mBx=1mCx=3mDx=4m
A single conservative force F(x) acts on a 1.0−kg particle that moves along the x-axis. The potential energy U(x) is given by U(x)=20+(x−2)2 where x is in meters. At x=5.0m, the particle has a kinetic energy of 20J.
The maximum and minimum values of x, respectively, are
View SolutionA particle of mass 2 kg moving along x-axis has potential energy given by, U=16x2−32x ( in joule), where x is in metre. Its speed when passing through x=1is2ms−1
View SolutionA single conservative force F(x) acts on a 1.0−kg particle that moves along the x-axis. The potential energy U(x) is given by U(x)=20+(x−2)2 where x is in meters. At x=5.0m, the particle has a kinetic energy of 20J.
What is the mechanical energy of a system?
View SolutionA single conservative force F(x) acts on a 1.0−kg particle that moves along the x-axis. The potential energy U(x) is given by U(x)=20+(x−2)2 where x is in meters. At x=5.0m, the particle has a kinetic energy of 20J.
Determine the equation of F(x) as a function of x.
View SolutionA single conservative f(x) acts on a m=1kg particle moving along the x-axis. The potential energy U(x) is given by :
U(x)=20+(x−2)2
where x is in metres. At x=5m, a particle has kintetic energy of 20 J
The largest value of x will be:
View Solution
