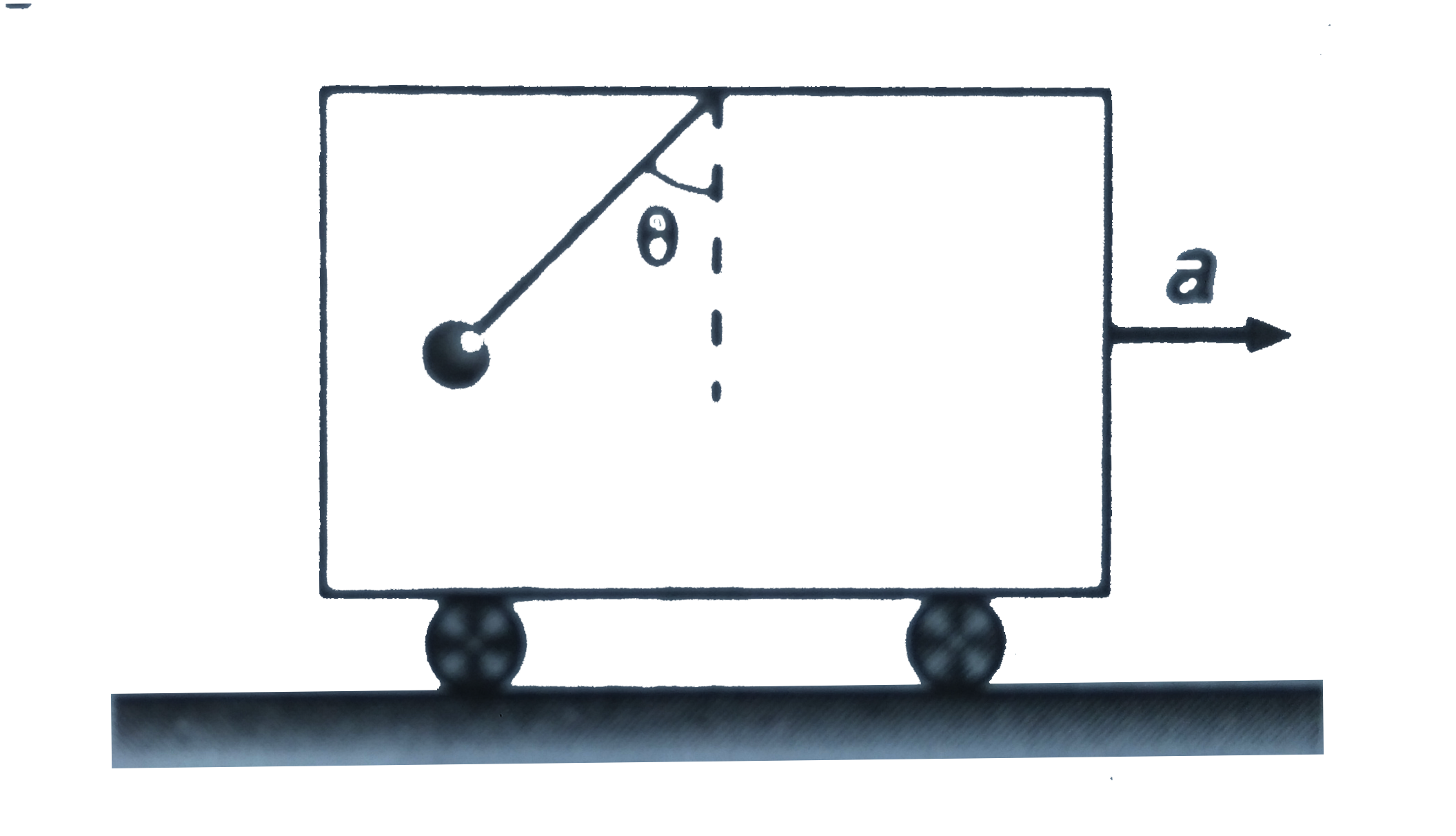
A car is moving on a horizontal road with constant acceleration 'a' . A bob of mass 'm' is suspended from the ceiling of car. The mean position about which the bob will oscillate is given by ('θ' is angle with vertical)
tanθ=ga
tanθ=ag
tanθ=2a9g
tanθ=a2g
The correct Answer is:2
To solve the problem, we need to determine the angle θ at which the bob of mass m will oscillate when the car is moving with a constant horizontal acceleration a. Here’s a step-by-step solution:
Step 1: Understand the Forces Acting on the Bob
When the car accelerates horizontally, the bob experiences two forces:
1. The gravitational force acting downwards, which is mg.
2. A pseudo force acting horizontally in the opposite direction of the car's acceleration, which is ma.
Step 2: Draw a Free Body Diagram
Visualize the situation:
- The bob is suspended from the ceiling of the car.
- The gravitational force acts vertically downward.
- The pseudo force due to the car's acceleration acts horizontally.
Step 3: Establish the Relationship between Forces
The bob will hang at an angle θ from the vertical. The forces can be represented as:
- The vertical component of the tension in the string balances the weight of the bob: Tcos(θ)=mg.
- The horizontal component of the tension balances the pseudo force: Tsin(θ)=ma.
Step 4: Divide the Two Equations
To eliminate T (the tension in the string), we can divide the two equations:
Tsin(θ)Tcos(θ)=mamg
This simplifies to:
tan(θ)=ag
Step 5: Solve for θ
To find the angle θ, we take the arctangent of both sides:
θ=tan−1(ag)
Conclusion
The mean position about which the bob will oscillate is given by the angle θ from the vertical, which is:
θ=tan−1(ag)
When the car accelerates horizontally, the bob experiences two forces:
1. The gravitational force acting downwards, which is mg.
2. A pseudo force acting horizontally in the opposite direction of the car's acceleration, which is ma.
Visualize the situation:
- The bob is suspended from the ceiling of the car.
- The gravitational force acts vertically downward.
- The pseudo force due to the car's acceleration acts horizontally.
The bob will hang at an angle θ from the vertical. The forces can be represented as:
- The vertical component of the tension in the string balances the weight of the bob: Tcos(θ)=mg.
- The horizontal component of the tension balances the pseudo force: Tsin(θ)=ma.
To eliminate T (the tension in the string), we can divide the two equations:
Tsin(θ)Tcos(θ)=mamg
This simplifies to:
tan(θ)=ag
To find the angle θ, we take the arctangent of both sides:
θ=tan−1(ag)
The mean position about which the bob will oscillate is given by the angle θ from the vertical, which is:
θ=tan−1(ag)
Topper's Solved these Questions
- OSCILLATIONSBOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT ( SECTION-C )
11 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT (SECTION -D( Comprehension) )
1 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT ( SECTION -A)
58 Videos
- NUCLEIBOOK - AAKASH INSTITUTECHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
- PHYSICAL WORLDBOOK - AAKASH INSTITUTECHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)
5 Videos
Similar Questions
A bob of mass m is suspended from the ceiling of a train moving with an acceleration a as shown in figure. Find the angle θ in equilibrium position.
View SolutionA car is moving in a circular horizontal track of radius 10 m with a constant speed of 10 m/s. A plumb bob is suspended from the roof of the car by a light rigid rod. What will be the angle made by the rod with the vertical? (g = 10 ms−2)
View Solution
Knowledge Check
A car is moving in a circular horizontal track of radius 10 m with a constant speed of 10ms−1. A plumb bob is suspended from the roof of the car by a string of length 1m. The angle made by the string with vertical is (g=10ms−2)
A0∘B30∘C45∘D60∘A simple pendulum with a bob of mass m is suspended from the roof of a car moving with horizontal acceleration a
AThe string makes an angle of tan−1(a/g) with the verticalBThe string makes an angle of sin−1(ag) with the verticalCThe tension in the string is m√a2+g2DThe tension in the string is m√g2−a2A simple pendulum with a bob of mass m is suspended from the roof of a car moving with a horizontal accelertion a. The angle made by the string with verical is
Atan−1(ag)Btan−1(1−ag)Ccos−1(ag)Dsin−1(ag)
A car is speeding up on a horizontal road with anaccelerationa. Consider the following situations in the car. i. A ball is suspended from the ceiling through a string and is maintaining a constant angel with the vertical. Find this angle. Ii. A block is kept on a smooth incline and does not slip on the incline. Find the angle of the incline with a horizontal.
View SolutionA plumb line is suspended from a celling of a car moving with horizontal acceleration of a. What will be the angle of inclination with vertical?
View SolutionA car is moving with constant speed of 10m/s on a horizontal circular path of radius 10√3m . A bob of mass m suspended through a light string from the roof of the car. What is the angle made by the string with the vertical if the bob is stationary with respect to the car? (g = 10 m/s2)
View SolutionA plumb line is suspended from a ceiling of a car moving with horizontal acceleration of a . What will be the angle of inclination with vertical
View SolutionA bus is moving in a circular horizontal track of radius 10 m with a constant speed 10m/s. A plumb bob is suspended from the roof of length 1.0m. The angle made by the rod with the track is (take g=10m/s2)
View Solution
