The magnetic field at the origin due to a current element I (→dl)placedataposi→n(→r)is
((μ0i4π) →dl×→rr3⎞⎠
⎛⎝−⎛⎝(μ0)i4π⎛⎝→r×→dlr3⎞⎠⎞⎠⎞⎠
⎛⎝(μ0)i4π⎛⎝→r×→dlr3⎞⎠⎞⎠
⎛⎝−⎛⎝(μ0)i4π→dl×→rr3⎞⎠⎞⎠
The correct Answer is:C, D
Step by step video, text & image solution for The magnetic field at the origin due to a current element I (vec dl ) placed at a positon (vec r) is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMACHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Exercises
61 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMACHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Objective 1
12 Videos
- MAGNETIC FIELDBOOK - HC VERMACHAPTER - MAGNETIC FIELDEXERCISE - Exercises
61 Videos
- MAGNETIC PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Exercises
9 Videos
Similar Questions
Find the magnitude of the magnetic field at the origin O due to very long conductor carrying current I of the shape as shown in figure.
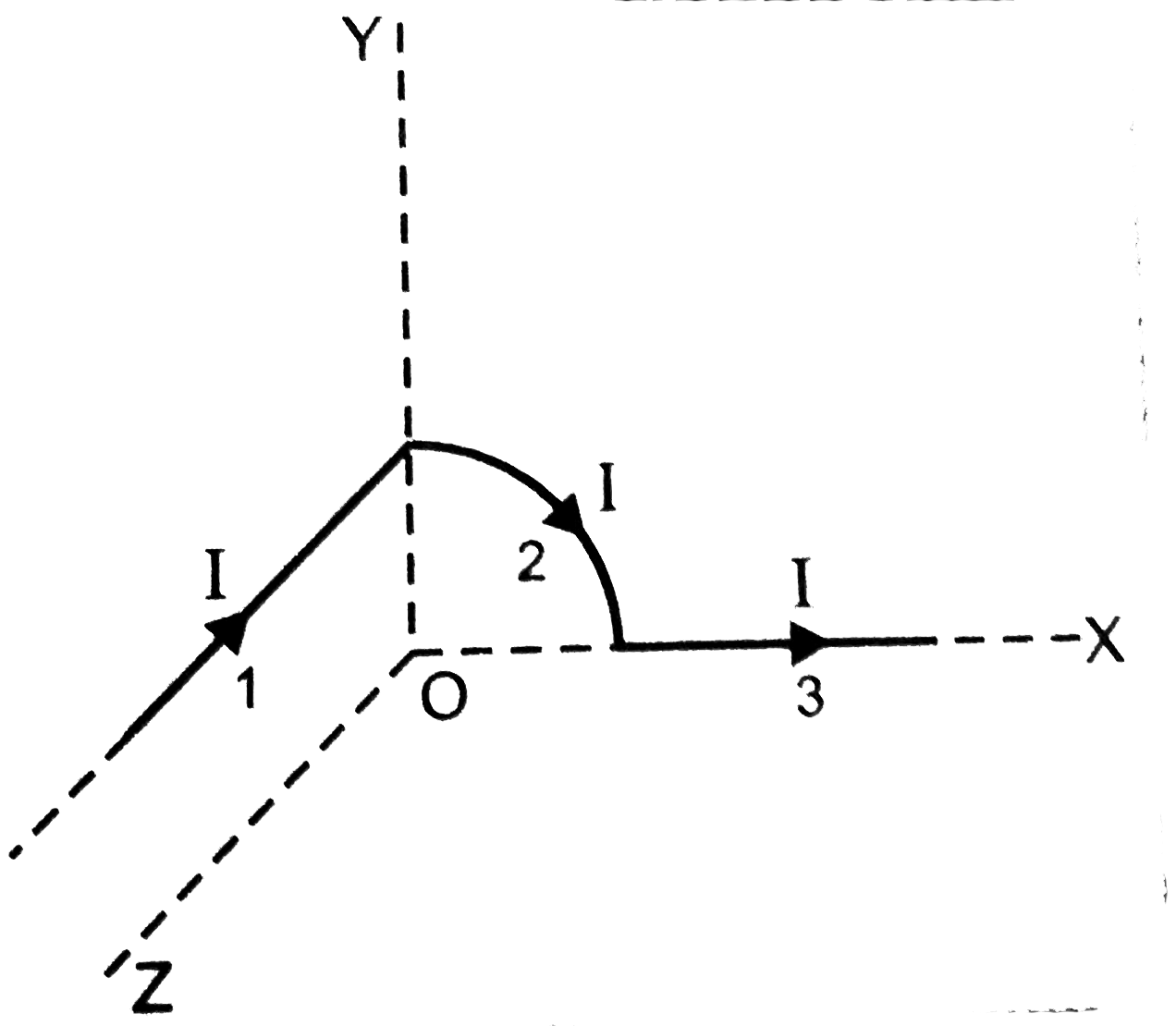
View SolutionFind the magnetic field at the ccentre of a current carrying conductor bent in the form of an arc subtending angle θ at its centre. Radius of the arc is R
Strategy: Let the arc lie in x-y plane with its centre at the origin. Consider a small current element i→dl as shown. The field due to this element at the centre can be obtained by Biot-Savart law
View Solution
Knowledge Check
The magnetic field at the origin due to a current element I→dl placed at position r is
(i) (μ0i4π)(d→l×→rr3)
−(μ0i4π)(d→l×→rr3)
(iii) (μ0i4π)(→r×d→lr3)
−(μ0i4π)(→r×d→lr3)A(i),(ii)B(ii),(iii)C(i),(ii)D(iii),(iv)The magnetic field at the origin due to the current flowing in the wire is
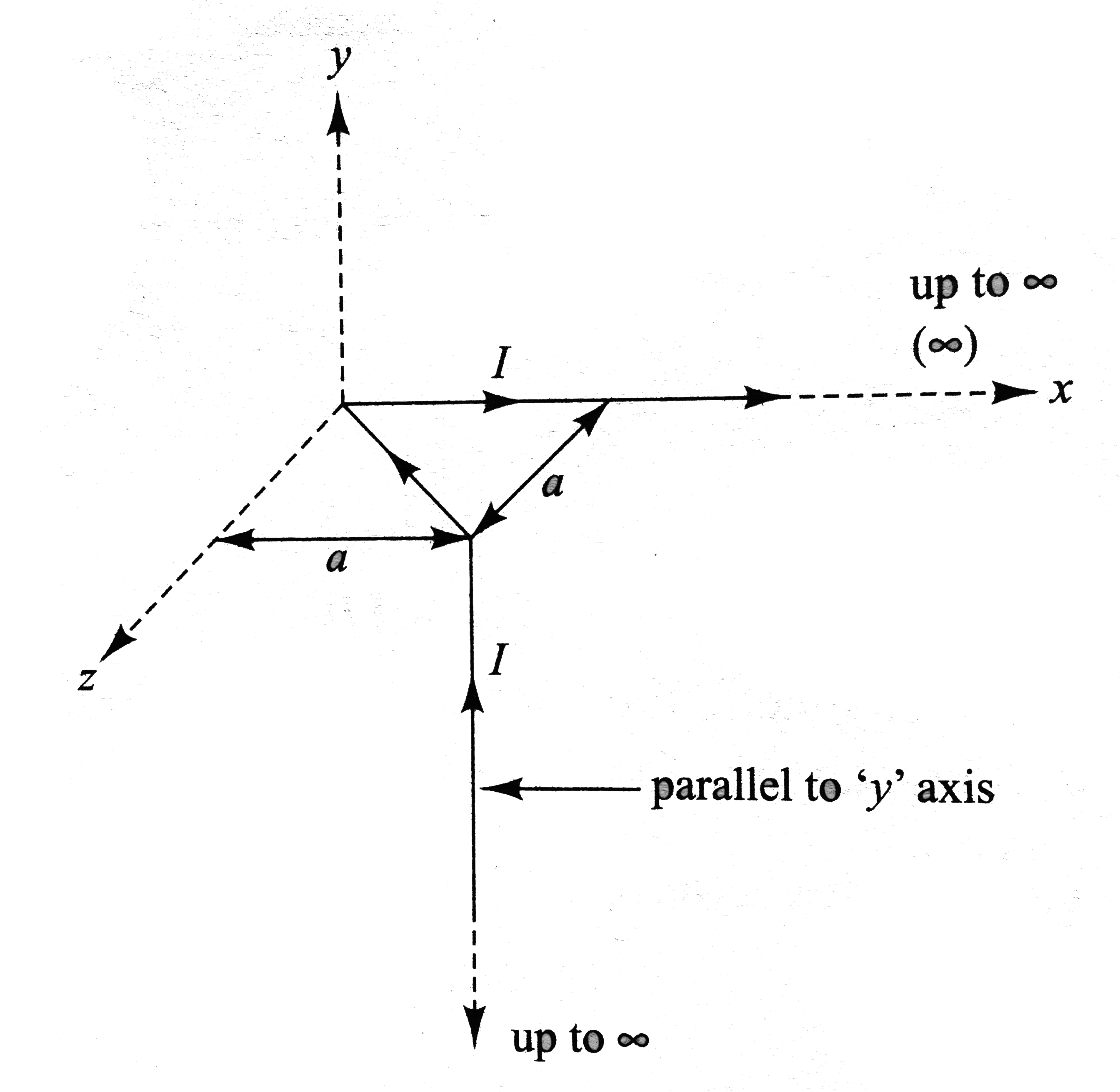 A−μ0I8πa(ˆi+ˆk)Bμ0I2πa(ˆi+ˆk)Cμ0I8πa(−ˆi+ˆk)D−μ0I4πa√2(ˆi−ˆk)
A−μ0I8πa(ˆi+ˆk)Bμ0I2πa(ˆi+ˆk)Cμ0I8πa(−ˆi+ˆk)D−μ0I4πa√2(ˆi−ˆk)The magnetic field ¯¯¯¯¯dB due to a small current element ¯¯¯dl at a distance →r and carrying current 'I' is
A¯¯¯¯¯dB=μ04πi(¯¯¯dlׯrr)B¯¯¯¯¯dB=μ04πi2(¯¯¯dlׯrr2)C¯¯¯¯¯dB=μ04πi2(¯¯¯dlׯrr)D¯¯¯¯¯dB=μ04πi(¯¯¯dlׯrr3)
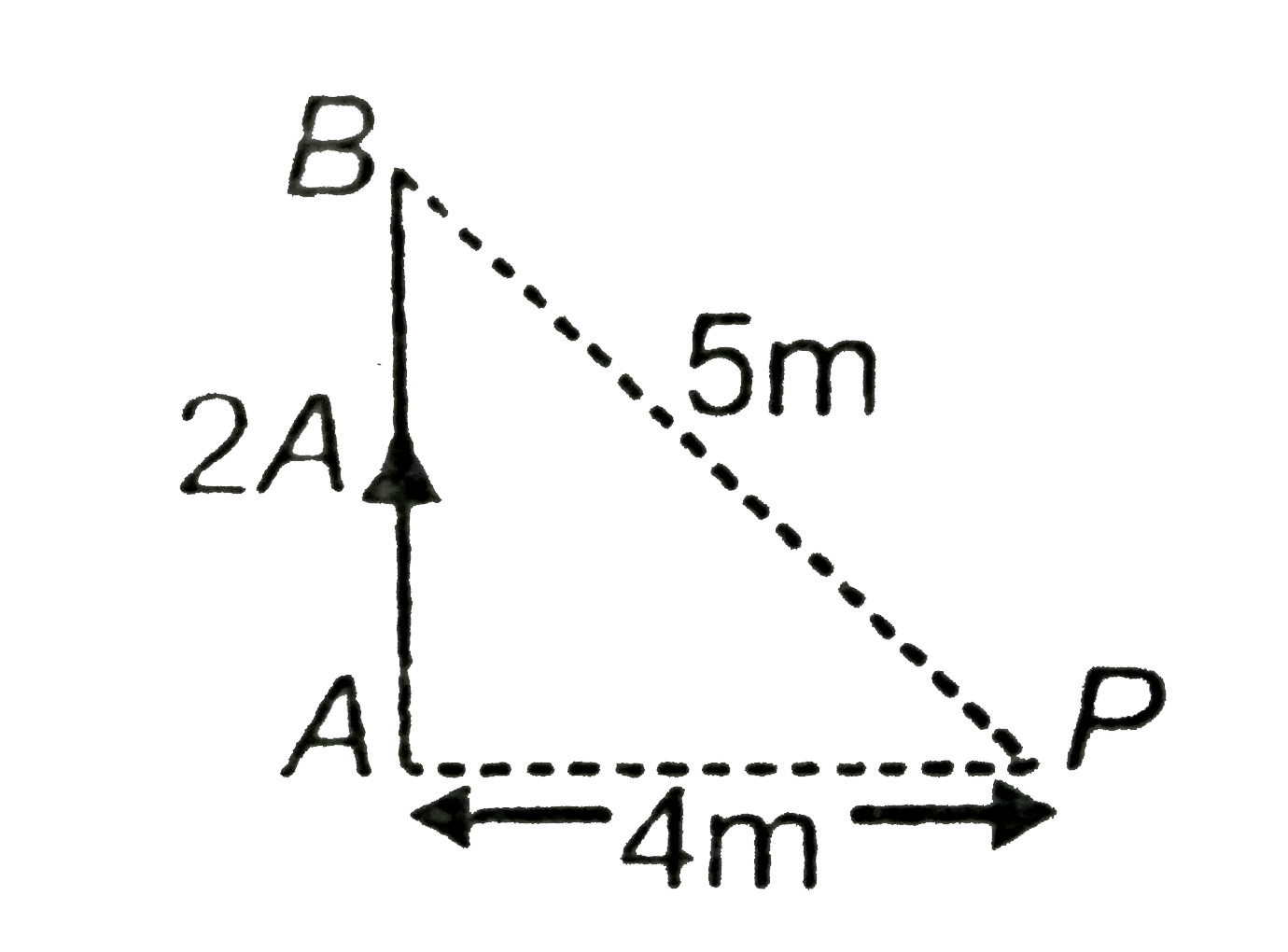
What is the magnetic field ∣∣→B∣∣ at the point P due to a current carrying wire of length AB (having a current of 2A) shown in figure ?
View SolutionState the Biot-Savart's law for the magnetic field due to a current carrying element. Use this law to obtain a formula for magnetic field at the centre of a circular loop of radius R carrying a steady current I, sketch the magnetic field lines for a current loop clearly indicating the direction of the field.
View Solution(a) State Bio-Savart's law in vector form expressing the magnetic field due to an element →dl carrying current I at a distance r from the element.
(b) Write the expression for the magnitude of the magnetic field at the centre of a circular loop of radius 'R' carrying a steady current I. Draw the field lines due to the current loop.
View SolutionThe magnetic field −→dB due to a small current element →dl carrying a current I at a distance →r is given as
View SolutionThe magnetic field d→B due to a small current element d→l at a distance →r and element carrying current i is,
View Solution
