An electron revolves around a proton in a hydrogen atom in an orbit of radius r. Considering the wave nature of electron and assuming that electron is present in the form of a stationary wave. Show that the angular momentum of the electron is quantized.

Video Solution

Text Solution

Verified by Experts

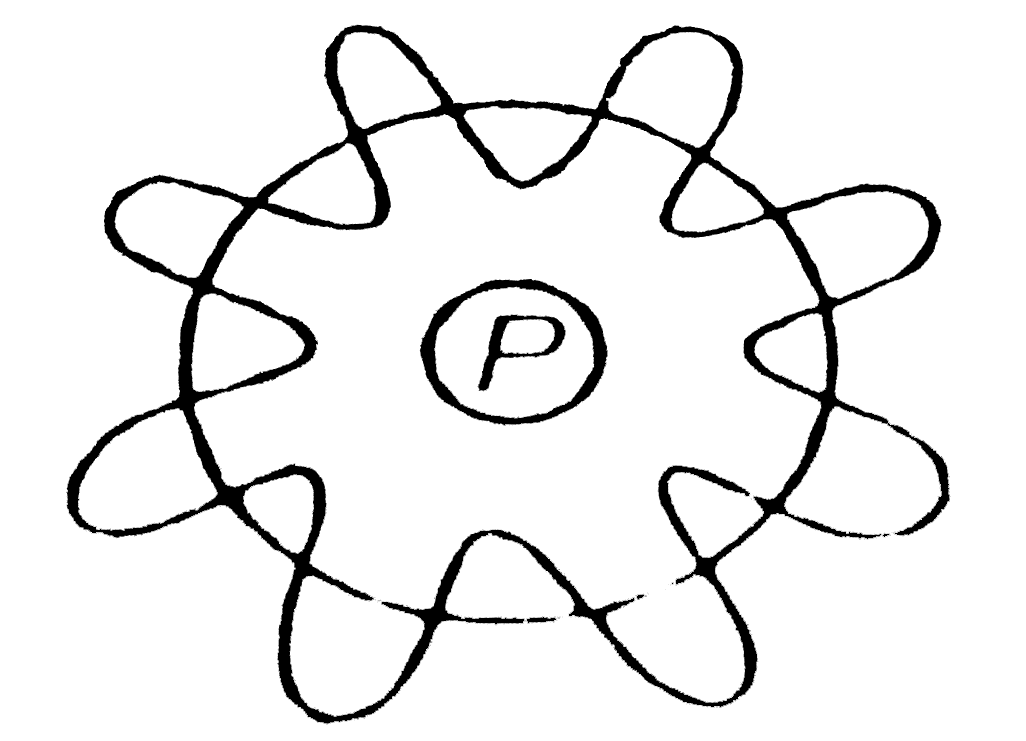
For a stationary wave shown,
$2 π r = n λ$
Also $λ = \frac{h}{mv}$ [de Broglie wavelength ]
$\Rightarrow 2 π r = \frac{nh}{mv}$
$\Rightarrow m v r = \frac{nh}{2 π}$
$\Rightarrow$ Angular momentum is quantized.

|

Updated on:21/07/2023

Class 12 PHYSICS ATOMS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The angular momentum of an electron in an orbital is given as:
A $L = n (\frac{n}{2 π})$
B $L = l (\frac{h}{2 π})$
C $L = \sqrt{l (l + 1)} (\frac{h}{2 π})$
D $L = m (\frac{h}{2 π})$
Question 2 - Select One
The minimum orbital angular momentum of the electron in a hydrogen atom is
A $h$
B $h / 2$
C $h / 2 π$
D $h / λ$
Question 3 - Select One
An electron makes transition inside a hydrogen atom. The orbital angular momentum of the electron may change by
A $h$
B $\frac{h}{3 π}$
C $\frac{h}{2 π}$
D $\frac{h}{4 π}$

AAKASH INSTITUTE-ATOMS-ASSIGNMENT SECTION J (Aakash Challengers )

Home
Ask Doubt
Profile